إحصاء ماكسويل وبولتزمان
تعتمد هذه المقالة اعتماداً كاملاً أو شبه كامل على مصدر وحيد. (ديسمبر 2018) |
إحصاء ماكسويل وبولتزمان (Maxwell–Boltzmann statistics) في الفيزياء والميكانيكا الإحصائية يصف هذا الإحصاء توزيع الجسيمات (مثل ذرات أو جزيئات غاز طبقا لما تحتوي عليه من طاقة حركة في حالة التوازن الحراري ، وذلك في ظروف درجات الحرارة العالية وانخفاض الكثافة حتى يمكن إهمال التأثيرات الكمومية.[1]
ويعطينا إحصاء ماكسويل-بولتزمان عدد الجسيمات ذات طاقة مقدارها بالمعادلة:
حيث:
- عدد الجسيمات الموجودة في الحالة i للطاقة
- هي مقدار الطاقة في الحالة i
- هو انفطار (فيزياء) مستوي الطاقة i وهو يعطي عدد المستويات التحتية للطاقة
- μ الجهد الكيميائي
- k ثابت بولتزمان
- T درجة الحرارة المطلقة كلفن
- N العدد الكلي للجسيمات في النظام (الموجود في حالة التوازن الحراري
- Z دالة توزيع الجسيمات
- e(...) الدالة الأسية للأساس الطبيعي e.
وتصاغ معادلة ماكسويل-بولتزمان أحيانا في الصورة:
حيث:
i مستوى الطاقة المنفطر وليس حزمة من مستويات الطاقة المنفطرة المكونة ل .
تفسير[عدل]
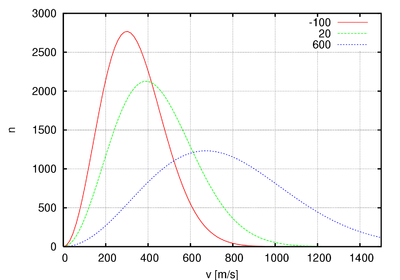
إذا وجد نظام مكون من عدد كبير من الجسيمات (مثل ذرات غاز أو جزيئاته) في حالة التوازن الحراري عند درجة حرارة ثابته فإن الذرات تتخذ توزيعا معينا بالنسبة إلى سرعاتها. فسرعات الذرات في النظام لا تكون متساوية، بل يوجد منها السريع والبطيئ وهي في ذلك تتبع قانونا يصفه إحصاء ماكسويل-بولتزمان. ومن صفات ذلك التوزيع أنه يتميز بقمة بين السرعات تسمى السرعة المتوسطة ينتمي إليها عدد كبير من ذراتالغاز في النظام (أنظر الشكل أعلاه). يعطينا المنحنى الأحمر توزيع سرعات الذرات في النظام عند درجة حرارة -100 درجة مئوية، ومنها نستنتج السرعة المتوسطة للقمة وقدرها 300 متر/الثانية. فإذا رفعنا درجة حرارة النظام إلى درجة 20 مئوية وانتظرنا بعض الوقت إلى أن يحدث التوازن الحراري بين الذرات (يحدث التوازن الحراري في النظام عن طريق تصادم الذرات بعضها البعض فتقل سرعة السريعة منها وتزداد سرعات بعض الذرات البطيئة وذلك عند درجة حرارة ثابته وتستقر النظام باتخاذه توزيع ماكسول-بولتزمان للسرعات) ، وجدنا أن توزيع سرعات الذرات عند درجة 20 مئوية تتخذ شكل المنحني الأخضر، ويتسم التوزيع بزيادة الإتساع كما يتسم بانزياح السرعة المتوسطة نحو سرعة متوسطة أعلى تبلغ في الشكل نحو 400 متر في الثانية عند درجة 20 مئوية.
فإذا رفعنا درجة حرارة النظام إلى 600 درجة مئوية تستجيب الذرات وتتبع توزيع المنحنى الأزرق، ويلاحظ زيادة اتساع توزيع السرعات مرة أخرى وانزياح سرعته المتوسطة إلى نحو 670 متر/ثانية.
- مع ملاحظة أنه لحساب توزيع سرعات الذرات في النظام باستخدام معادلة ماكسويل-بولتزمان فإننا نعوّض في المعادلة عن درجة الحرارة المطلقة بالكلفن، وهي تزيد عن درجة الحرارة المئوية بإضافة 273 درجة إليها. أي أن المنحني الأخضر مميز لدرجة حرارة 293 كلفن.
حدود تطبيقه[عدل]
يعتبر إحصاء ماكسويل-بولتزمان أنه لا توجد تأثيرات (تجاذبية مثلا) بين الذرات بعضها البعض في النظام وهذه هي حالة خاصة يتصف بها الغاز المثالي. ولكن إحصاء ماكسويل-بولتزمان يستخدم في حالات كثير بمثابة تقريب للحقيقة عند التعامل مع الغازات، لكنه لا يصلح لوصف الذرات أو الجزيئات في السوائل.
وينطبق نظام ماكسويل-بولتزمان على الغازات المثالية، أي القليلة الكثافة بحيث نستطيع إهمال التآثر بين الذرات وعند درجات الحرارة العالية. أما في درجات الحرارة المنخفضة فيصف النظام إحصاء بوز-أينشتاين بدقة أكبر بالنسبة لنظام مكون من البوزونات أو احصاء فيرمي ديراك بالنسبة لنظام فرميونات.
ويمكن مقارنة الثلاثة إحصاءات بتبسيطها إلى إحصاء ماكسويل-بولتزمان بوضع :
فينتج :
اقرأ أيضا[عدل]
مراجع[عدل]
- ^ Tolman، R. C. (1938). The Principles of Statistical Mechanics. Dover Publications. ISBN:9780486638966.









