قوة نووية ضعيفة
| جزء من سلسلة مقالات حول |
| النموذج المعياري لفيزياء الجسيمات |
|---|
 |
القوة النووية الضعيفة[1][2] أو القوة الضعيفة أو التآثر الضعيف هي واحدةٌ من القوى الأساسية الأربعة الموجودة في الطبيعة حسب فيزياء الجسيمات، إلى جانب ثلاث قوى أخرى هي التآثر القوي، والتآثر الكهرومغناطيسي، والجاذبية. تُعد القوة النووية الضعيفة القوّة المسؤولة عن الاضمحلال الإشعاعي والانشطار النووي للجسيمات دون الذرية، وتُسمّى نظرية القوة النووية الضعيفة في بعض الأحيان باسم الديناميكا النكهية الكمية قياساً على مُصطلحي ديناميكا لونية كمية وكهروديناميكا كمية، لكنّ هذا المُصطلح نادر الاستخدام عملياً.[3]
تنتج القوة النووية الضعيفة عن انبعاثات أو امتصاصات بوزونات دبليو وزد طبقاً للنموذج القياسي لفيزياء الجسيمات، وتتآثر جميع الفرميونات المعروفة تآثراً ضعيفاً. والفرميونات هي جُسيمات تملك خاصية اللف المغزلي بعدد كم مغزلي قيمته نصف عدد صحيح. يُمكن أن يكون الفرميون جُسيماً أولياً مثل الإلكترون، ويُمكن أن يكون جُسيماً مُركباً مثل البروتون. وبما أنّ كتلة بوزونات دبليو وزد أكبر بكثير من كتلة البروتونات والنيوترونات، فإنّ هذا يخلق مدى قصيراً للقوة النووية الضعيفة. وتعود سبب تسمية هذا التآثر بالضعيف إلى أنّ شدة مجاله على مدى مسافة مُعينة تكون أقل حجماً من تلك التي يصنعها التآثر القوي والتآثر الكهرومغناطيسي.
انقسمت قوة التآثر الكهروضعيف إلى قوتي التآثر الكهرومغناطيسي والقوة النووية الضعيفة خلال حقبة الكوارك. يظهر أثر القوة النووية الضعيفة في الطبيعة في ظاهرة الاضمحلال التي تُصيب مُعظم الفرميونات مع مرور الوقت، ومن الأمثلة المُهمة على ذلك اضمحلال بيتا، وكذلك إنتاج الديوتريوم ومن ثمّ الهيليوم من ذرة الهيدروجين ممّا يؤدي إلى حدوث الاندماجات النووية في الشمس. يُمكنّنا هذا الاضمحلال من التأريخ بالكربون المشع، حيث أنّ النظير كربون-14 يضمحلّ بوساطة القوة النووية الضعيفة إلى النظير نيتروجين-14.[4]
توجد الكواركات - التي تُشكّل الجُسيمات المُركبة مثل البروتونات والنيوترونات - على شكل ست «نكهات»: علوي، وسفلي، وغريب، وساحر، وقمّي، وقعري، وتُعطي هذه الجسيمات خواصها المُميّزة. تتفرد القوة النووية الضعيفة من حيث أنها تسمح للكواركات في تغيير نكهاتها من نكهة إلى أخرى، فمثلاً يتحول كوارك سفلي إلى آخر علوي أثناء اضمحلال بيتا ليُصبح بذلك النيوترون بروتوناً. وبالإضافة إلى ذلك فإنّ القوة النووية الضعيفة هي القوة الوحيدة بين القوى الأساسية التي تخرق التكافؤ وكذلك الوحيدة التي تستطيع خرق تناظر الشحنة السوية.
التاريخ[عدل]
اقترح الفيزيائي الإيطالي الأمريكي إنريكو فيرمي عام 1933 النظرية الأولى عن القوة النووية الضعيفة، والمعروفة باسم تآثر فيرمي. حيث أشار فيرمي في نظريته إلى أنّه يُمكن تفسير اضمحلال بيتا على أنّه تفاعل أربع فرميونات مع بعضها البعض مُتضمناً قوة تماس لا نطاق لها.[5][6]
لكنّ الوصف الأفضل لهذه القوة هو أنها قوة عدم التماس ذات نطاق محدود، وإن كان قصيراً جداً. وحّد شيلدون جلاشو، ومحمد عبد السلام، وستيفن واينبرج عام 1968 القوتين الكهرومغناطيسية والضعيفة وبيّنوا أن هاتين القوتين هما جانبين من قوة واحدة، وهي التي تُسمّى الآن القوة الكهروضعيفة.[7] ولم يؤكد وجود بوزونات دبليو وزد قطعاً حتى عام 1983.[8]
الخصائص[عدل]

للقوة النووية الضعيفة خصائصٌ تُميّزها عن القوى الأساسية الأخرى، وهي:
- أنها القوة الوحيدة القادرة على تغيير نكهة الكواركات.
- أنها القوة الوحيدة التي تخرق التكافؤ وتستطيع خرق تناظر الشحنة السوية.
- تُحمل هذه القوة بوساطة جُسيمات ناقلة تُعرف باسم بوزون مقياس، وتختلف عن بقيّة القوى من حيث أنّ الجسيمات الناقلة لها تكون ذات كتل هائلة، على العكس من بقية الجسيمات الناقلة التي تكون بلا كتلة، ويُمكن تفسير هذه الميّزة في النموذج القياسي بوساطة آلية هيغز.
تمتاز هذه الجسيمات الناقلة بقصر أجلها بسبب كتلتها الكبيرة التي تُعادل حوالي 90 غيغا إلكترون فولت/س2، حيث س تمثل سرعة الضوء،[9] حيث أنّ مدى حياة هذه الجسيمات - التي تُعرف باسم بوزونات دبليو وزد - أقل من 1 × 10- 24 ثانية فقط.[10] للقوة النووية الضعيفة ثابت ربط (وهو مؤشر على قوة التآثر) يتراوح مقداره بين 10- 7 و10- 6، بينما يبلغ ثابت ربط التآثر القوي حوالي 1، أما للقوة الكهرومغناطيسية فيبلغ حوالي 10- 2،[11] وبالتالي فإنّ القوة النووية الضعيفة ضعيفة من حيث القوة.[12] كما أنّ مدى القوة النووية الضعيفة قصيرٌ جداً (حوالي 10- 17 إلى 10- 16 متر)،[12] فعندما تكون المسافة حوالي 10- 18 متر تكون قوة القوة النووية الضعيفة مُماثلةً للقوة الكهرومغناطيسية، ولكن على مسافة حوالي 3 × 10- 17 متر تكون قوة القوة النووية الضعيفة أضعف بعشرة آلاف مرة من نظيرتها الكهرومغناطيسية.[13]
تؤثر القوة النووية الضعيفة على جميع الفرميونات في النموذج القياسي، فضلاً عن تأثيرها على بوزون هيغز، حيث أنّ النيوترينوات تتآثر بوساطة الجاذبية والقوة النووية الضعيفة فقط، وهي التي كانت السبب الأساسي في تسمية القوة النووية الضعيفة بهذا الاسم.[12] لا علاقة للقوة النووية الضعيفة بطاقة الارتباط، بَيْد أنّ الجاذبية تُشكّل مصدراً لهذه الطاقة على المستوى الفلكي، والقوة الكهرومغناطيسية على المستوى الذري، والتآثر القوي على المستوى النووي.[14]
أهمُّ ما يُميّز القوة النووية الضعيفة هو خاصيّتها الأولى المُتمثلة في تغيير نكهات الكواركات. فالنيوترون على سبيل المثال أثقلُ من البروتون، لكنّه لا يستطيع أن يتحول إلى بروتون إلا بتغيير نكهة (نوع) أحد كواركيْه السفليين ليصبح كواركاً علوياً وبذلك يصير بروتوناً، ولا يُمكن أن تتم هذه العملية بوساطة التآثر القوي ولا بوساطة القوة الكهرومغناطيسية، بل تتم بوساطة الاضمحلال الضعيف الذي يتسبب في عدم استقرار جميع الميزونات.[15] ولولا وجود القوة النووية الضعيفة ما استطاعت الكواركات تغيير نكهاتها، وبالتالي كانت خصائص الكواركات ستُحفظ دون تغيير في جميع التفاعلات. فأثناء عملية اضمحلال بيتا يتحول كوارك سفلي في النيوترون إلى كوارك علوي من خلال إطلاق جسيم افتراضي يُدعى بوزون (W-)، الذي يتحول بعد ذلك إلى إلكترون ونقيض نيوترينو إلكتروني.[16]
الاضمحلال الضعيف أقلُّ حصولاً في الطبيعة من القوي أو الكهرومغناطيسي بسبب ضخامة كتلة البوزون، وبالتالي فإنّه أقل سرعة أيضاً. فالبيون المُتعادل على سبيل المثال يضمحلّ كهرومغناطيسياً، لذا فإنّ دورة حياته تُقارب 10- 16 ثانية فقط، بينما يعيش البيون المشحون (الذي يضمحلّ بوساطة القوة النووية الضعيفة) قُرابة 10- 8 ثانية، أي أطول بمائة مليون مرة من نظيره المُتعادل.[17] وكذلك يعيش النيوترون الحر (الذي يضمحلّ أيضاً بوساطة القوة النووية الضعيفة) حوالي 15 دقيقة.[16]
اللف النظائري الضعيف[عدل]
| الجيل الأول | الجيل الثاني | الجيل الثالث | ||||||
|---|---|---|---|---|---|---|---|---|
| الفرميون | الرمز | اللف النظائري الضعيف |
الفرميون | الرمز | اللف النظائري الضعيف |
الفرميون | الرمز | اللف النظائري الضعيف |
| إلكترون | ميوون | تاوون | ||||||
| إلكترون نيوترينو | ميوون نيترينو | تاو نيترينو | ||||||
| كوارك علوي | كوارك ساحر | كوارك قمي | ||||||
| كوارك سفلي | كوارك غريب | كوارك قعري | ||||||
| قيمة اللف النظائري الضعيف لجميع الجسيمات المضادة العسراء يساوي صفر. الجسيمات المضادة اليمنى تملك قيمة اللف النظائري الضعيف المُعاكسة. | ||||||||
لدى جميع الجُسيمات خاصيةٌ تُدعى اللف النظائري الضعيف (T3)، وهي عدد كمي يتحكم في كيفية تآثر الجُسيم تآثراً ضعيفاً، أي أنّه بمثابة الشحنة الكهربائية في التآثر الكهرومغناطيسي أو الشحنة اللونية في التآثر القوي. تكون قيمة اللف النظائري الضعيف في جميع الفرميونات +1⁄2، كما هو الحال في الكوارك العلوي، أو -1⁄2 كما هو الحال في الكوارك السفلي على سبيل المثال. ولا يُمكن أن يضمحلّ كوارك إلى كوارك آخر له نفس قيمة اللف النظائري الضعيف بوساطة القوة النووية الضعيفة، بل يُشترط اختلاف الإشارة بين القيمتين حتى يحصل الاضمحلال.
اللف النظائري الضعيف محفوظٌ في التفاعلات كافّة، حيث يكون مجموع قيم اللف النظائري للجسيمات الداخلة في التفاعل مُساوٍ لمجموع قيم اللف النظائري للجسيمات الخارجة من التفاعل. فمثلاً يضمحلّ البيون الأعسر - عدد اللف النظائري له 1 - إلى ميوون نيترينو (+1⁄2) وميوون (+1⁄2).[17]
أنواع التآثر[عدل]
هناك نوعان من القوة النووية الضعيفة: النوع الأول يُدعى تآثر التيار المشحون، وذلك لأنه يحدث بوساطة جسيمات تحمل شحنة كهربائية (بوزونات دبليو الموجبة أو السالبة)، وهو المسؤول عن ظاهرة اضمحلال بيتا. أمّا النوع الثاني فيُدعى تآثر التيار المحايد، وذلك لأنه يحدث بوساطة جسيمات مُتعادلة كهربائياً (بوزونات زد).
تآثر التيار المشحون[عدل]
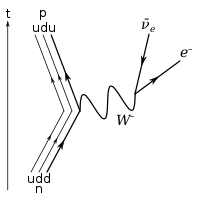
من الأمثلة على تآثر التيار المشحون هو ما يحدث عندما يحصل ليبتون مشحون (مثل الإلكترون أو الميون ذويْ الشحنة -1) على بوزون دبليو ذي الشحنة +1 ليصير بذلك نيوترينو (شحنته صفر) مُناظراً لليبتون، حيث أنّ نوع النيوترينو (إلكترون أو ميون أو تاو) يكون نفس نوع الليبتون الذي تآثر. مثل:
ومن الأمثلة على ذلك أيضاً إمكانية تُحوّل كوارك سفلي (ذي الشحنة −1⁄3) إلى كوارك علوي (ذي الشحنة +2⁄3) عن طريق التخلص من بوزون دبليو سالب الشحنة أو الحصول على بوزون دبليو موجب الشحنة. كما يُمكن أن يتخلص كوارك علوي من بوزون دبليو موجب الشحنة أو أن يحصل على بوزون دبليو سالب الشحنة ليصير كواركاً سفلياً:
وبما أنّ بوزونات دبليو غير مُستقرة فإنّ دورة حياتها تكون قصيرةً جداً وتضمحلّ سريعاً، مثل:
ويُمكن أن تضمحلّ بوزونات دبليو إلى جُسيمات أخرى، لكن باحتمالات مُتفاوتة.[19]
يتمثّل تآثر التيار المشحون أيضاً فيما يُعرف باضمحلال بيتا للنيوترون، حيث يتخلص كوارك سفلي داخل النيوترون من بوزون دبليو سالب ليصير كواركاً علوياً، وليصير النيوترون بذلك بروتوناً. وبسبب الطاقة المُشاركة في العملية (أي فرق الكتلة بين الكوارك السفلي والعلوي) فإنّ بوزون دبليو السالب لا يُمكن أن يتحول سوى إلى إلكترون ونقيض نيوترينو إلكتروني.[20] يُمكن تمثيل هذه العملية هكذا:
تآثر التيار المحايد[عدل]
يتخلص الكوارك أو الليبتون من بوزون زد عديم الشحنة أو يحصلان عليه في تآثر التيار المحايد، مثل:
ويضمحلّ بوزون زد سريعاً حاله حال بوزون دبليو،[19] مثل:
نظرية التآثر الكهروضعيف[عدل]
يصف النموذج القياسي لفيزياء الجسيمات التآثرين الكهرومغناطيسي والضعيف على أنهما وجهان لقوة واحدة هي قوة التآثر الكهروضعيف، وهي نظرية ظهرت لأول مرة قرابة عام 1968 على يد شيلدون جلاشو، ومحمد عبد السلام، وستيفن واينبرج، وحصل الثلاثة على جائزة نوبل في الفيزياء عام 1979 تكريماً لعملهم.[21] وتوفر آلية هيغز تفسيراً لوجود البوزونات المقياسية الثلاثة الضخمة (الحاملات الثلاثة للقوة النووية الضعيفة) والفوتون عديم الكتلة في التآثر الكهرومغناطيسي.[22]
وفقاً لهذه النظرية، فإنّه لدى الكون عندما تكون مُستويات الطاقة عاليةً جداً أربع مجالات لبوزونات مقياس عديمة الكتلة، لكن عندما تكون مُستويات الطاقة مُنخفضةً فإنّ التناظر القياسي يُكسر تلقائياً مُتسبباً في إنتاج ثلاثة بوزونات عديمة الكتلة، لكنّ هذه البوزونات تتآثر مع ثلاث مجالات شبيهة بمجال الفوتون (من خلال آلية هيغز) لتحصل على كتلتها. هذه المجالات الثلاثة تُصبح بوزون دبليو الموجب والسالب وبوزون زد في القوة النووية الضعيفة، في حين أنّ المجال الرابع يظلّ عديم الكتلة وهو الفوتون في التآثر الكهرومغناطيسي.[22]
وضعت هذه النظرية عدة تنبؤات، منها التنبؤ بكتلة بوزونات دبليو وزد قبل اكتشافها. وفي 4 يوليو 2012 أعلن فريقا أطلس وسي إم إس في مصادم الهدرونات الكبير بشكلٍ مُستقلٍ الاكتشاف الرسمي لبوزون لم يكن معروفاً مُسبقاً تتراوح كتلته بين 125 - 127 إلكترون فولت/س2 ويتوافق سلوكه إلى حد كبير مع بوزون هيغز، لكنهم كانوا بحاجة إلى المزيد من البيانات والتحاليل للتأكد قبل الإعلان عن أنّ هذا البوزون هو بالفعل بوزون هيغز. وفي 14 مارس 2013 أُكِّد وجود بوزون هيغز مبدئياً.[23]
خرق التناظر[عدل]

اعتُقد لفترة طويلة أنّ قوانين الطبيعة لا تتغير بالانعكاس في مرآة، أي بعكس جميع المحاور المكانية، وهذا ما يُعرف بقانون انحفاظ التكافؤ. أثبت هذا القانون صحته فيما يتعلّق بالجاذبية والتآثر الكهرومغناطيسي والتآثر القوي، لذا افتُرض أن يكون قانوناً كونيّاً.[24] استمر هذا الاعتقاد حتى مُنتصف الخمسينيّات، عندما طرح تشين يانج وتسونج لي فكرة أنّ القوة النووية الضعيفة قد تخرق هذا القانون. وفي عام 1957 اكتشفت تشين شيونغ وو أن القوة النووية الضعيفة تخرق التكافؤ فعلاً، ليحصل بذلك يانج ولي على جائزة نوبل في الفيزياء عام 1957.[25]
كانت القوة النووية الضعيفة تُفسر عن طريق نظرية فيرمي سابقاً، لكنّ اكتشاف خرق التكافؤ غيّر من هذا المفهوم وبات العلماء بحاجة إلى نهجٍ جديد. وفي عام 1957 جاء روبرت مارشاك وجورج سودرشان، وفي وقت لاحق ريتشارد فاينمان وموري جيلمان بنظرية جديدة للقوة النووية الضعيفة. تحصل القوة النووية الضعيفة وفقاً لهذه النظرية على الجسيمات العسراء (أو الجسيمات المضادة اليمنى)، فبما أنّ انعكاس جسيم أعسر في مرآة هو جسيم أيمن، إذاً فإنّ هذه النظرية نجحت في تفسير خرق التكافؤ. جاءت هذه النظرية قبل اكتشاف العلماء لبوزونات زد، لذا فإنها لم تشمل ما يحدث في تآثر التيار المحايد.
لكنّ النظرية السابقة قالت بانحفاظ الشحنة السويّة (CP). يُمثل الحرف P التكافؤ (التحول من اليسار إلى اليمين)، أمّا الحرف C فيُمثل الشحنة (التحول بين الجسيمات والجسيمات المضادة). تفاجأ الفيزيائيون مُجدداً عام 1964 حينما قدّم جيمس كرونين وفال فيتش أدلةً واضحةً بأنّ اضمحلال الكاون يخرق تناظر الشحنة السويّة، وحازا باكتشافهما هذا على جائزة نوبل في الفيزياء عام 1980.[26] أظهر ماكوتو كوباياشي وتوشيهيده ماساكاوا عام 1973 أنّ خرق تناظر الشحنة السويّة في القوة النووية الضعيفة يتطلب أكثر من جيلين من الجسيمات،[27] أي أنهما تنبّأا بوجود جيل ثالث من الجسيمات لم يكن معروفاً حينها. وأدى هذا الاكتشاف إلى حصولهما على نصف جائزة نوبل في الفيزياء عام 2008.[28]
انظر أيضًا[عدل]
| قوة نووية ضعيفة في المشاريع الشقيقة: | |
| |
المراجع[عدل]
- ^ القوة النووية الضعيفة والبحث عن الشحنة الضعيفة للبروتونات، الباحثون السوريون [وصلة مكسورة] نسخة محفوظة 04 مايو 2014 على موقع واي باك مشين.
- ^ عالمنا اللامتناظر،مجلة العلوم نسخة محفوظة 29 مارس 2016 على موقع واي باك مشين.
- ^ Griffiths، David (2009). Introduction to Elementary Particles. ص. 59–60. ISBN:978-3-527-40601-2.
- ^ "The Nobel Prize in Physics 1979: Press Release". NobelPrize.org. Nobel Media. مؤرشف من الأصل في 2017-12-04.
- ^ Fermi, Enrico (1934). "Versuch einer Theorie der β-Strahlen. I". Zeitschrift für Physik A. ج. 88 ع. 3–4: 161–177. Bibcode:1934ZPhy...88..161F. DOI:10.1007/BF01351864.
- ^ Wilson, Fred L. (ديسمبر 1968). "Fermi's Theory of Beta Decay". American Journal of Physics. ج. 36 ع. 12: 1150–1160. DOI:10.1119/1.1974382.
- ^ electroweak-theory - Encyclopedia Britannica نسخة محفوظة 29 أبريل 2015 على موقع واي باك مشين.
- ^ The discovery of 'heavy light' نسخة محفوظة 19 أغسطس 2017 على موقع واي باك مشين.
- ^ W.-M. Yao et al. (Particle Data Group) (2006). "Review of Particle Physics: Quarks" (PDF). Journal of Physics G. ج. 33: 1. arXiv:astro-ph/0601168. Bibcode:2006JPhG...33....1Y. DOI:10.1088/0954-3899/33/1/001. مؤرشف من الأصل (PDF) في 2017-01-25.
- ^ Peter Watkins (1986). Story of the W and Z. Cambridge: Cambridge University Press. ص. 70. ISBN:978-0-521-31875-4. مؤرشف من الأصل في 2015-01-03.
- ^ "Coupling Constants for the Fundamental Forces". HyperPhysics. Georgia State University. مؤرشف من الأصل في 2018-09-26.
- ^ أ ب ت J. Christman (2001). "The Weak Interaction" (PDF). Physnet. Michigan State University. مؤرشف من الأصل (PDF) في 2012-03-16.
- ^ "Electroweak". The Particle Adventure. Particle Data Group. مؤرشف من الأصل في 2018-10-08.
- ^ Walter Greiner؛ Berndt Müller (2009). Gauge Theory of Weak Interactions. Springer. ص. 2. ISBN:978-3-540-87842-1. مؤرشف من الأصل في 2014-11-29.
- ^ Cottingham & Greenwood (1986, 2001), p.29
- ^ أ ب Cottingham & Greenwood (1986, 2001), p.28
- ^ أ ب Cottingham & Greenwood (1986, 2001), p.30
- ^ Baez، John C.؛ Huerta، John (2009). "The Algebra of Grand Unified Theories". Bull.Am.Math.Soc. ج. 0904: 483–552. arXiv:0904.1556. Bibcode:2009arXiv0904.1556B. مؤرشف من الأصل في 2018-08-14.
- ^ أ ب K. Nakamura et al. (Particle Data Group) (2010). "Gauge and Higgs Bosons" (PDF). Journal of Physics G. ج. 37. مؤرشف من الأصل (PDF) في 2017-02-15.
- ^ K. Nakamura et al. (Particle Data Group) (2010). "n" (PDF). Journal of Physics G. ج. 37: 7. مؤرشف من الأصل (PDF) في 2018-10-03.
- ^ "The Nobel Prize in Physics 1979". NobelPrize.org. Nobel Media. مؤرشف من الأصل في 2018-08-13.
- ^ أ ب C. Amsler et al. (Particle Data Group) (2008). "Review of Particle Physics – Higgs Bosons: Theory and Searches" (PDF). Physics Letters B. ج. 667: 1. Bibcode:2008PhLB..667....1P. DOI:10.1016/j.physletb.2008.07.018. مؤرشف من الأصل (PDF) في 2018-10-03.
- ^ "New results indicate that new particle is a Higgs boson | CERN". Home.web.cern.ch. مؤرشف من الأصل في 2015-10-20.
- ^ Charles W. Carey (2006). "Lee, Tsung-Dao". American scientists. Facts on File Inc. ص. 225. ISBN:9781438108070. مؤرشف من الأصل في 2015-01-20.
- ^ "The Nobel Prize in Physics 1957". NobelPrize.org. Nobel Media. مؤرشف من الأصل في 2018-06-15.
- ^ "The Nobel Prize in Physics 1980". NobelPrize.org. Nobel Media. مؤرشف من الأصل في 2018-05-31.
- ^ M. Kobayashi, T. Maskawa (1973). "CP-Violation in the Renormalizable Theory of Weak Interaction". Progress of Theoretical Physics. ج. 49 ع. 2: 652–657. Bibcode:1973PThPh..49..652K. DOI:10.1143/PTP.49.652.
- ^ "The Nobel Prize in Physics 1980". NobelPrize.org. Nobel Media. مؤرشف من الأصل في 2018-07-25.
مصادر خارجية[عدل]
- R. Oerter (2006). The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics. Plume. ISBN:978-0-13-236678-6.
- B.A. Schumm (2004). Deep Down Things: The Breathtaking Beauty of Particle Physics. Johns Hopkins University Press. ISBN:0-8018-7971-X.
- D.A. Bromley (2000). Gauge Theory of Weak Interactions. Springer. ISBN:3-540-67672-4.
- G.D. Coughlan, J.E. Dodd, B.M. Gripaios (2006). The Ideas of Particle Physics: An Introduction for Scientists (ط. 3rd). Cambridge University Press. ISBN:978-0-521-67775-2.
{{استشهاد بكتاب}}: صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link) - W. N. Cottingham؛ D. A. Greenwood (1986, 2001). An introduction to nuclear physics (ط. 2). Cambridge University Press. ص. 30. ISBN:978-0-521-65733-4. مؤرشف من الأصل في 2015-02-02.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|سنة=(مساعدة) - D.J. Griffiths (1987). Introduction to Elementary Particles. John Wiley & Sons. ISBN:0-471-60386-4.
- G.L. Kane (1987). Modern Elementary Particle Physics. Perseus Books. ISBN:0-201-11749-5.
- D.H. Perkins (2000). Introduction to High Energy Physics. Cambridge University Press. ISBN:0-521-62196-8.

























