دالة هاش تشفيرية

دالة هاش تشفيرية (على وجه التحديد، SHA-1) في العمل. لاحظ أن حتى التغيرات الصغيرة في المصدر في الدخل (هنا في كلمة "over") یؤدي الى تغيير جذري في الخرج الناتج، يتم ذلك بفعل ما يسمى أثر الإنهيار الجليدي

.

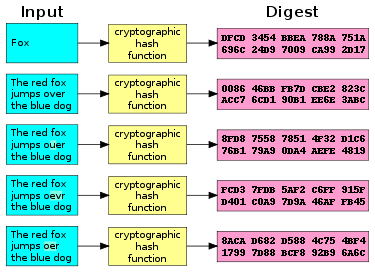
دالة هاش التشفيرية هي دالة هاش, بمعنى انها تأخذ اي عدد من قطع البيانات وتعيد سلسلة ثابتة الطول من البتات تسمى قيمة هاش التشفيرية، بحيث ان اي تغيير في البيانات الاصلية (عرضيا او متعمدا) سوف يؤدي إلى تغيير كبير في قيمة هاش التشفيرية (باحتمال كبير جدا). عادة تسمى البيانات المشفرة "الرسالة" ومقدار هاش التشفيري يسمى الخلاصة digest.

هذا النوع من الخوارزميات لا يحتاج إلى مفتاح تشفير لانه لا يستخدم لتشفير النصوص وانما للتأكد من ان محتوى الرسالة موثوق ولم يتم التعديل عليه. وذلك بمقارنة الخلاصة المرسلة مع الخلاصة المولدة من الرسالة المطلوب التأكد من صحة محتواها.

من الامثلة على دالة هاش التشفيرية خوارزميات MD5 و Tiger و SHA-1.

تمتلك دالة هاش التشفيرية المثالية اربع صفات اساسية:

• يمكن حساب خلاصة بسهولة لاي رسالة معطاة
• انه من غير الممكن توليد رسالة انطلاقا من خلاصة معطاة
• انه من غير الممكن تغيير رسالة من دون ان تتغير خلاصتها
• انه من غير الممكن توليد رسالتين لهما نفس الخلاصة

لدالات هاش التشفيرية تطبيقات عديدة في مجال أمن المعلومات, وخصوصا في الامضاءات الرقمية, رموز استيقان الرسائل MAC, وانواع الاستيقان الاخرى لاكتشاف المعلومات المكررة او ملفات الكيانات

الخصائص

تم نصميم اغلب دالات هاش التشفيرية لتأخذ سلسلة من المحارف من اي طول وتعيد قيمة هاش ثابتة الطول ان دالة هاش التشفيرية يجب ان تقاوم كل انواع هجوم تحليل التشفير المعروفة. وبالحد الادنى يجب ان تتمتع بالخصائص التالية:

• مقاومة العكس او Preimage resistance

  بفرض قيمة هاش $h\,$ يجب ان يكون من الصعب ايجاد رسالة $m\,$ بحيث يكون $h=\mathrm{hash}(m)\,$.

يرتبط هذا المبدأ ب الدالات وحيدة الاتجاه او غير العكوسة. الدالات التي تفتقر لهذه الصفة تكون معرضة لهجوم العكس.

• مقاومة العكس الثاني او Second-preimage resistance

  بفرض وجود دخل او ورودي $m_1\,$ يجب ان يكون من الصعب ان نجد دخلا اخر $m_2\,$ حيث $m_1 \ne m_2\,$ بحيث يكون $\mathrm{hash}(m_1) = \mathrm{hash}(m_2)\,$.

يشار احيانا إلى هذه الخاصية بـِ مقاومة العكس الضعيف والدالات التي تفتقر لهذه الصفة تكون معرضة لهجوم العكس الثاني.

• مقاومة التصادم او Collision resistance

  يجب ان يكون من الصعب ايجاد رسالتين مختلفتين $m_1\,$ و $m_2\,$ بحيث يكون $\mathrm{hash}(m_1) = \mathrm{hash}(m_2)\,$.

يطلق على زوج كهذا تصادم الهاش. يشار احيانا إلى هذه الخاصية بـِ مقاومة العكس القوي. يجب ان يكون طول قيمة الهاش على الاقل ضعف الطول المطلوب لمقاومة العكس, والا فستوجد التصادمات ب هجوم عيد الميلاد او Birthday attack.

تقتضي هذه الخصائص بأن العدو سيئ القصد لا يستطيع ان يستبدل او يغير بيانات الدخل بدون تغيير خلاصتها. وبالتالي, فاذا كان لدينا سلسلتين تملكان نفس الخلاصة, فانه يمكت الاطمئنان باتهما متطابقتان.

الدالة التي تملك هذه الخصائص ربما تكون ما نزال تملك خصائصا غير مستحبة. ان دالات الهاش التشفيرية الحالية معرشة لهجوم تمديد الطول: بفرض $h(m)\,$ و $\mathrm{len}(m)\,$ ولكن ليس $m\,$, باختيار $m'\,$ مناسب يمكن للمهاجم ان يحسب $h (m||m')\,$ بحيث $||$ تعني الوصل. يمكن استخدام هذه الخاصة لكسر طرق الاستيقان الاولية التي تعتمد على دالات الهاش. ان تركيب HMAC يتغلب على هذه المشاكل .

انظر ايضاً

• برمجيات حاسوب
• امن الحاسوب
• التوقيع الالكتروني
• لعبة البوكر العقلية
• رمز الاستجابة السريعة
• حماية أقراص الدفيدي من النسخ .