رمز شليفلي

متعدد السطوح الاثنا عشري
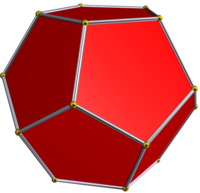
(بالإنجليزية: dodecahedron)‏ هو متعدد سطوح منتظم يرمز له برمز شليفلي {3,5} بالعربية أو {5,3} باللاتينية، لأن له 3 مخمسات حول كل من رؤوسه.

رمز شليفلي في الهندسة الرياضية هو عبارة عن ترميز للأشكال الهندسية يأخذ الشكل {ض، ط، ق، ...} أو {p,q,r,...}. و يستخدم لتعريف متعددات الجوانب المنتظمة والمُرَصّعَات.

أطلق على هذا الترميز اسم رمز شليفلي نسبة إلى مبتكره عالم الرياضيات لودفيغ شليفلي (بالإنجليزية: Ludwig Schläfli)‏ الذي كانت له اسهامات هامة في الهندسة الرياضية ومجالات أخرى في القرن التاسع عشر.

وصف الترميز

رمز شيلفلي هو وصف تِكراري للأشكال الهندسية، يبدأ بعدد يرمز لمضلع منتظم عدد أضلاعة ض بالرمز {ض} ( أو {p} باللاتينية). على سبيل المثال، الرمز {3} يرمز لمثلث متساوي الأضلاع، والرمز {4} يرمز للمربع وهلم جرا.

أما متعدد الوجوه (السطوح) الذي يتشكل من عدد ط ( أو q باللاتينية) من الوجوه تلتقى عند كل رأس من رؤوسه، ويكون كل وجه منها هو عبارة عن مضلع منتظم عدد أضلاعه ض فيرمز له بالرمز {ض، ط} أو {p,q}. فمثلاً يكون ترميز المكعب هو {3,4} أو {4,3} لوجود ثلاث مربعات حول كل رأس من رؤوس المكعب.

ويتم تمثيل متعدد المقام الرباعى الأبعاد أو متعدد المقام-4 ( polytope-4 )، الذي يتكون من عدد ق {ض، ط} من الخلايا المنتظمة حول كل حافة من حوافه بالرمز {ض، ط، ق} أو {p,q,r} ، وهلم جرا. وتكون كل خلية من خلايا متعدد المقام رباعى الأبعاد هي عبارة عن متعدد وجوه ذا أحرف متجهه.

يمكن أن تتشكل متعددات المقام المنتظمة من عناصر لها شكل مضلع نجمي، مثل النجمة الخماسية، التي يرمز لها بالرمز {5\2} أو {5/2}، وهي نجمة لها رؤوس ممثلة في رؤوس خماسي منتظم ولكن أضلاعها متصله بالتناوب بين تلك الرؤوس.

وبوجه عام، فان سطيح متعدد المقام {ض، ط، ق،....س، ع} هو {ض، ط، ق،....س}.

أيضاً بنية الرأس لمتعدد المقام المنتظم تكون شكلاً هندسياً منتظماً. وتكون بنية الرأس لمتعدد المقام المنتظم {ض، ط، ق،....س، ع} هي {ط، ق،....س، ع}.

رمز شيلفلي يمكن أن يستخدم لتمثيل أي متعدد سطوح محدب متناهي الشكل، وأى مُرَصّعْ متناهي الشكل في الفراغ الإقليدي، أو أي مُرَصّعْ لا متناهي الشكل في الفراغ الزائدي اعتماداً على الخلل الزاوي للبناء الهندسي. فعندما يكون الخلل الزاوي موجباً فانه يسمح لبنية الرأس أن تنثني لتدخل في بعد فراغي أعلى وتنعقد (أو تدور) راجعة مرة أخرى إلى نفسها كمتعدد مقام. أما الخلل الزاوي صفر فهو يُرَصّعْ الفراغ كسطيحات هندسية في نفس الأبعاد الفراغية. وعندما يكون الخلل الزاوي سلبياً فهو لا يمكن أن يتواجد في الفراغ العادي، ولكن يمكن بناؤه في الفراغ الزائدي.

وعادة ما يفترض في بنية الرأس أنها متعدد مقام متناهي الأبعاد، ولكن يمكن أن تعتبر في بعض الأحيان على أنها مُرَصْعَة هندسية في حد ذاتها.

كذلك، كل متعدد المقام يكون له متعدد مقام مزدوج، تمثله عناصر رمز شليفلي في ترتيبها العكسي. ومتعدد المقام ذاتي الازدواج يكون له «رمز شليفلي» متماثل.

مجموعات التماثل

يرتبط رمز شليفلي ارتباطاً وثيقاً بمجموعات التماثل أو التناظر الانعكاسي، التي تدعى أيضاً مجموعات كوكستر، وهي تُعطى بنفس العلامات، ولكن داخل أقواس مربعة [ض، ط، ق، ....] أو [p,q,r,...]. وغالباً ما تسمي تلك المجموعات حسب اسم متعددات المقام المنتظمة التي تتولد عنها. على سبيل المثال [3,3] أو [3,3] هي مجموعة كوكستر للتماثل رباعي السطوح (بالإنجليزية: Tetrahedral symmetry)‏ ، و[4,3] أو [3,4] هو التماثل ثماني السطوح (بالإنجليزية: Octahedral symmetry)‏، و [5,3] أو [3,5] هو التماثل عشروني السطوح (بالإنجليزية: Icosahedral symmetry)‏.

المضلعات المنتظمة (مستوى)

رمز شليفلي للمضلع المنتظم ذو الحواف ن هو {ن} أو {n} باللاتينية.

على سبيل المثال، يتم تمثيل الخماسي المنتظم بالرمز {5} أو {5}.

راجع المضلع المنتظم المحدب والمضلع النجمي الغير محدب.

على سبيل المثال، {5\2} أو {5/2} هو رمز النجمة الخماسية.

متعددات الوجوه/السطوح المنتظمة (فراغ ثلاثي الأبعاد)

رمز شليفلي لمتعدد الوجوه المنتظم هو {ض، ط} إذا كانت وجوهه هي مضلعات منتظمة لها عدد أضلاع ض، وتحيط بكل رأس من رؤوسه عدد ط من تلك الوجوه (وتكون بنية الرأس أيضاً مضلع منتظم عدد أضلاعة ط).

على سبيل المثال {3,5} أو {5,3} هو رمز متعدد السطوح الاثنا عشري المنتظم. فهو مكون من وجوه على شكل خماسي منتظم (5 حواف)، و 3 خماسيات منتظمة حول كل رأس من رؤوسه.

راجع المجسمات الأفلاطونية الخمس المحدبة، ومتعددات وجوه كبلر-بوينسوت الأربعة الغير محدبة.

ويمكن أيضاً استخدام رموز شليفلي لتعريف المُرَصّعْات المنتظمة في الفراغ الإقليدي أو الزائدي بطريقة مماثلة.

على سبيل المثال، يتم تمثيل القَرْمَدة السداسية بالرمز {3,6} أو {6,3}.

مراجع

• إيريك ويستاين، رمز شليفلي، ماثوورلد Mathworld (باللغة الإنكليزية).