معادلة شرودنغر
| معادلة شرودنغر | |
|---|---|
 |
|
| الصيغة | |
| سميت باسم | إرفين شرودنغر |
| تعديل مصدري - تعديل | |
| جزء من سلسلة مقالات حول |
| ميكانيكا الكم |
|---|
| بوابة ميكانيكا الكم |
في ميكانيكا الكم، معادلة شرودنغر عبارة عن معادلة تفاضلية جزئية تصف كيفية تغير الحالة الكمية لنظام فيزيائي مع الزمن، وقد صاغها عالم الفيزياء النمساوي إرفين شرودنغر في أواخر عام 1925 ونشرها عام [1] 1926.
تصف هذه المعادلة حالات النظم الكمومية المعتمدة على الزمن. وتحتل هذه المعادلة أهمية خاصة في ميكانيكا الكم حيث تعتبر بمثابة قانون التحريك الثاني لنيوتن الذي يعتبر أساسيا في الفيزياء الكلاسيكية.
حسب التعبير الرياضي لميكانيكا الكم، تترافق كل جملة فيزيائية مع فضاء هلبرت المركب (المعقد) (وهو عبارة عن فضاء شعاعي) حيث توصف كل حالة لحظية للجملة بشعاع وحدة في هذا الفضاء الشعاعي، وبالتالي يكون شعاع الحالة بمثابة ترميز لاحتمالات النتائج الممكنة من عمليات القياس بكافة أشكالها على هذه الجملة. عندما تتغير هذه الجملة مع الزمن، يصبح شعاع الحالة (دالة زمنية).
المعادلات[عدل]
المعادلة المعتمدة على الزمن[عدل]

فيما يلي معادلة شرودنغر المعتمدة على الزمن (في شكلها العام)
في هذه المعادلة تعني دالة موجية تصف النظام الكمومي (نظام صغري مثل حجم الذرة)، و وحدة تخيلية، و ثابت بلانك المخفض، و معامل هاميلتوني يصف الطاقة الكلية لكل دالة موجية معتبرة وهو يتخذ عدة صور تعتمد على المسألة الفيزيائية المراد حلها.
معادلة شرودنجر المعتمدة على الزمن في حالة جسيم يتحرك حركة توافقية تحت تأثير مجال:
تتكون المعالة إلى اليمين من جزئين: الجزء الأول: وهو يمثل مؤثر طاقة الحركة للجسيم، والجزء الثاني وهو يمثل مؤثر الطاقة الكامنة للجسيم في المجال التوافقي (مثل مجال نواة الذرة). المجال التوافقي موصوف بالدالة التي تعتمد على الزمن والمكان .

وتتعامل معاملة شرودنجر مع الجسيم (إلكترون مثلا) الذي يتحرك في مجال نواة (مشحونة) على أنه في هيئة دالة موجية:
معتمدة على الزمن والموقع ، حيث يعطي حل المعادلة صفات الجسيم وما يمكن له أن يمتلكه من طاقة.
أي أن معادلة شرودنجر تماثل معادلة هاميلتون التي تعطي الطاقة الكلية لجسيم في هزاز توافقي في الحالة الكلاسيكية (ميكانيكا نيوتن ومعادلات ماكسويل)، وأما معادلة شرودنجر فهي تعطي الطاقة الكلية للجسيم الذي يتحرك في مجال توافقي كمومي.
لم تنجح معادلة هاميلتون في التعامل مع جسيمات صغرية على المستوى الذري فلم تأتي بحلول صحيحة لحركة الإلكترون في مجال شحنة النواة، وكان ذلك عند دراسة الطيف الضوئي من الهيدروجين. فكانت الحلول لا تتفق مع القياسات التي نحصل عليها عمليا. ذلك بعكس ميكانيكا الكم والممثلة هنا بمعادلة شرودنجر فقد استطاعت إعطاء الحلول المتفقة مع القياسات المعملية وذلك باعتبار أن الجسيم يكون في هيئة موجة مادية وليس جسما ماديا.
هذا هو عالم الذرات وتآثرها ببعضها البعض وهو عالم غريب عن العالم الذي اعتدنا عليه عند التعامل مع أجسام ذات أبعاد كبيرة ككرة الجولف أو كرة البلياردو أو عالم الكواكب والأجرام السماوية. مع تلك الأبعاد الكبيرة تصلح ميكانيكا نيوتن في إعطاء الحلول السليمة لتلك الأنظمة الكبيرة، أما عند التعامل مع عالم الذرات والجسيمات الأولية فلا بد من استخدام معادلات ميكانيكا الكم فهي وحدها (حتى الآن) التي تعطي حلولا سليمة لتلك الأنظمة الصغرية.
المعادلة التي لا تعتمد على الزمن[عدل]
تعتبر معادلة شرودنجر المعتمدة على الزمن أن الدوال الموجية يمكن أن تكوّن موجات راكدة تسمى «حالات مستقرة» (أي تسمى «أوربيتال» كما هو الحال في حالة مدارات الإلكترونات حول نواة الذرة أو في مدارات الجزيئات، هذه الحالات تلعب دوراً هاماً في التركيب الذري والجزيئي)، وعلاوة على ذلك تصنف الحالات المستقرة وتفهم، ويصبح من السهل حل معادلة شرودنجر المعتمدة على الزمن لأي حالة أخرى.
ومعادلة شرودنجر غير المعتمدة على الزمن هي التي تصف الحالات المستقرة. وتستعمل عندما يكون الهاميلتوني نفسه غير معتمداً على الزمن، وأنما تكون معتمدة على المكان فقط.
معادلة شرودنجر غير المعتمدة على الزمن (الحالة العامة)
نقرأ هذه المعادلة هكذا:
- " عندما يؤثر معامل هاميلتون على الدالة الموجية فربما تكون النتيجة متناسبة طردياً مع نفس الدالة الموجية ، فإذا كانت كذلك فتكون حالة مستقرة، ويعطي ثابت التناسب طاقة الحالة . "
وتتميز تلك المعادلة رياضياً بأنها تعطي معادلة قيم ذاتية Eigenvalue Equation عن النظام.
ومن أهم معادلات شرودنجر التي تصف جسيماً يتحرك في مجال كهربائي (وليس في مجال مغناطيسي) هي:
معادلة شرودنجر غير المعتمدة على الزمن، فهي تعتمد على المكان فقط (لجسيم يوجد في مجال نواة ذرية أو غير ذلك مثلما في حالة جسيم حر، ولا تأخذ في الاعتبار تأثيرات النظرية النسبية):
وقد سبق تعريف عناصر المعادلة أعلاه.
من أهم النتائج[عدل]
شكلت معدلة شرودنجر ونتائجها فتحا جديدا في فهم الفيزياء. فقد كانت معادلته الأولى من نوعها وأوصلت نتائجها العلماء إلى تبعات لم تتوقع من قبل وغير عادية في ذلك الوقت.
طاقة الحركة وطاقة الوضع والطاقة الكلية[عدل]
يمكن تفسير عناصر معادلة شرودنجر غير النسبية كالأتي:
- الطاقة الكلية = (طاقة الحركة) + (طاقة الوضع)
وفي ذلك فهي مشابهة للفيزياء الكلاسيكية. فمثلا تكون الطاقة الكلية للرقاص ثابتة، وتنخفض سرعته (أي تقل طاقة حركته) عندما يرتفع ويقترب من نقطة العودة في مجال الجاذبية الأرضية، وبعد بلوغه أعلى نقطة في مساره القوسي يتوقف لحظة ويبدأ العودة في اتجاه نقطة السكون وتتحول طاقة الوضع له إلى طاقة حركية ثانيا. ويكون مجموع طاقته الحركية وطاقة وضعه دائما ثابتا في كل لحظة.
الكمومية[عدل]
تتنبأ معادلة شرودنجر أنه إذا قمنا بقياس بعض خواص النظام فمن الممكن أن تكون القياسات «كمومية» بمعنى أن النتائج قد تكون على شكل قيم منفصلة "discrete values". فعلى سبيل المثال، «كمومية الطاقة»: تكون طاقة الإلكترون في الذرة دائما أحد الطاقات الكمومية، وهي ظاهرة اكتشفت عن طريق دراسة مطيافية الذرات. وهناك مثال آخر يتعلق بالزخم الزاوي فهو أيضا يكون كموميا، أي يمكنه اتخاذ قيم منفصلة. وقد كان ذلك مجرد فكرة في نموذج بور الابتدائي للذرة، ولكن معادلة شرودنجر تنبأت به فيما بعد.
القياسات ومبدأ عدم التأكد[عدل]
في الميكانيكا الكلاسيكية يكون لجسيم في جميع الأوقات في مكان محدد بدقة وله زخم حركة معينة دقيقة. وتحدد قوانين نيوتن للحركة بكل دقة تلك المواصفات الخاصة بالجسيم أثناء سيرها. أما في ميكانيكا الكم فلا يكون لجسيم مواصفات بالغة الدقة، وعندما نقوم بقياسها فتكون تلك النتائج موصوفة بتوزيع احتمالي. وتتنبأ معادلة شرودنجر بأن التوزيعات الاحتمالية لا تستطيع التعرف على النتيجة الدقيقة لكل عملية قياس.
وتمثل مبدأ عدم التأكد الذي صاغه العالم الفزيائي الألماني هايزنبرج مثالا شهيرا عن عدم التأكد في ميكانيكا الكم. وهذا المبدأ يقول أنه كلما زادت دقة معرفتنا لمكان جسيم فإن معرفتنا بزخم حركته تقل دقتها، والعكس بالعكس.
وتستطيع معادلة شرودنجر تعيين الدالة الموجية لجسيم بكل دقة، ولكن حتى معرفة دقيقة للدالة الموجية فإن نتيجة عملية قياس معينة على الدالة الموجية يكون محفوفا بدرجة من عدم التأكد.
النفق الكمومي[عدل]
في الفيزياء الكلاسيكية عندما تتدحرج كرة عاليا على جبل تقل سرعتها رويدا رويدا حتى تتوقف ثم تعود متدحرجة ثانيا إلى سفح الجبل، ذلك لأنها لم تمتلك طاقة كافية لكي تصعد فوق الجبل لتهبط من الناحية الأخرى. أما معادلة شرودنجر فهي تتوقع أنه يوجد احتمال ولو ضعيف أن تنتقل الكرة إلى الناحية الأخرى من الجبل حتى ولو كانت طاقتها الحركية لاتكفي لأن تصل إلى قمة الجبل. وهذا ما يسمي بالنفاذية خلال نفق كمومي، وهذه الظاهرة تنبع من مبدأ عدم التأكد: فمع أن الكرة تبدو وأنها موجودة على ناحية من الجبل إلا أن مكانها فيه ليس أكيدا، بحيث أنه يوجد احتمال لتواجدها على الناحية الأخرى من الجبل.
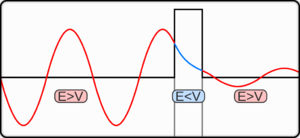

التغير الزمني لحزمة موجية كما تصفه حل معادلة شرودنجر في حالة نظام جهدي ذو قمة واحدة مبينا شرائح لمحوري المكان والزمن (ويبن المحور الثالث المطال وهو يعبر عن احتمال تواجد الجسيم في المكان المذكور). يبدو الجسيم كدوائر زرقاء وكثافتها اللونية تتناسب مع احتمال وجود الجسيم في الموقع المبين. ويمثل الخط النقطي الجهد الجبلي. واحتمال النفاذية أكبر من الانعكاس لأن الطاقة الكلية تزيد عن طاقة الوضع.
استنباط حديث لمعادلة شرودنجر[عدل]
صاغ شرودنجر عام 1926 معادلته واضعا فيها بعض المبادئ الفيزيائية التي تتكئ عليها بعض الظواهر الكمومية المعروفة في ذلك الوقت. وتعتمد رياضيات معادلة شرودنجر على مبدأ التواصل لدالة هاميلتون التي تعطي الطاقة الكلية:
وبالتعويض عن الطاقة وزخم الحركة والمكان في الميكانيكا الكلاسيكية باستخدام معاملات ميكانيكية كمومية:
ثم تطبيق الدالة الموجية ergibt التي كانت معروفة في علم البصريات:
- .
بهذا تحولت دالة هاميلتون إلى معامل هاميلتون Hamilton-Operator.
ومن الوجهة التاريخية طبق شرودنجر وصف دي برولي للجسيم الحر، وقام بتوليف متناظرات بين الفيزياء والموجات الكهرومغناطيسية في هيئة ازدواجية موجة-جسيم وتطبيق الصفات الموجية للجسيمات:
- ,
حيث ثابت.
تلك المعادلة الموجية هي عبارة عن أحد حلول معادلة شرودنجر وتحتوي على .
ويبقى مع ذلك التفسير الفيزيائي للدالة الموجية مفتوحا غير واضحا. وفي التفسيرات الإحصائية الجارية على ميكانيكا الكم تعطي مربع القيمة احتمال وجود الجسيم في موقع معين (وهذا هو تفسير ماكس بورن الألماني).
تفسير الدالة الموجية[عدل]
تسمح لنا معادلة شرودنجر لحساب الدوال الموجية لنظام وكيف تتغير مع الزمن. ولكن معادلة شرودنجر لا تقول «ما هي» الدالة الموجية بالضبط. وتعتني تفسيرات ميكانيكا الكم بأسئلة مثل العلاقة بين الدالة الموجية والحقيقة الواقعية ونتائج قياسات التجارب.
وبينما تحسب الميكانيكا التقليدية مسار لجسيم بدقة يظهر مكان الجسيم في ميكانيكا الكم كقيمة محتملة لدوال توزيع ، تعطيها معادلة شرودنجر. ويوصف الجسيم كحزمة موجية فإذا كان اتساع الحزمة الموجية قصيرا جدا فيمكن تحويل معادلة شرودنجر إلى معادلة نيوتن للحركة. . تصاغ الدوال الموجية في معادلة شرودنجر في صورة معاملات طبقا لتصور شرودنجر. وفي تصور هايزنبرج الذي حل مسألة طيف الهيدروجين بميكانيكا الكم فقد صاغ معادلات الحركة مباشرة بدلا من المعاملات. وتسمى طريقة هايزنبرج التي استخدم فيها حساب المصفوفات وتسمى «معادلات هايزنبرج للحركة». وكلا الطريقتين: معادلة شرودنجر أو معادلات الحركة لهايزنبرج متماثلتان من وجهة النتائج. وقد توصل هايزنبرج لطريقته عام 1923 أي قبل توصل شرودنجر لمعادلته التي صاغها عام 1926.
رفض أينشتاين ميكانيكا الكم باعتبارها لا تصف مكان جسيم بدقة مثلما في الميكانيكا الكلاسيكية وتعطي فقط احتمال وجود الجسيم في مكان معين ولكن التوافق بين طريقة هايزنبرج الكمومية ومعادلة شرودنجر والنجاح التي حازته ميكانيكا الكم في تفسير ظواهر طبيعية كثيرة تعجز الميكانيكا الكلاسيكية عن حسابها وتفسيرها ثبتت من مركز ميكانيكا الكم كطريقة يمكن الاعتماد عليها في تفسير الظواهر الطبيعية على المستوى الصغري في عالم الذرات والجزيئات والجسيمات الأولية.
الخلفية التاريخية وتطور معادلة شرودنجر[عدل]
بعد اكتشاف ماكس بلانك لكمومية الضوء (انظر اشعاع الجسم الأسود) وتفسير أينشتاين بأن تسمية «الكم» quanta الذي استخدمها بلانك هو عبارة عن فوتون أو «جسيم ضوئي»، واقترح اعتبار أن تكون طاقة الفوتون متناسبة مع تردده، فكانت تلك الفكرة من أول الافتراضات الخاصة بازدواجية الموجة والجسيم.
ونظرا لكون الطاقة وزخم الحركة ينتسبان إلى التردد والعدد الموجي في النظرية النسبية الخاصة، فينتج عن ذلك أن زخم الحركة للفوتون يكون متناسبا طرديا مع عدده الموجي .
وافترض لويس دي برولي أن هذا ينطبق على جميع الجسيمات، بما فيها الإلكترون. وبين انه بافتراض أن الموجة المادية تتقدم مزاملة لجسيمها، فإن الإلكترون يكوّن موجة راكدة، بمعنى أنه يحتوي على ترددات زاوية منفصلة فقط حول النواة الذرية وهي التي تكون مسموحة له باتخاذها.[2]
تلك المدارات الكمومية في الذرة تنتمي إلى مستويات طاقة منفصلة (أي لها قيم خاصة ذاتية)، واستطاع دي برولي تفسير نموذج بور للبنية الذرية وما تحويه من مستويات للطاقة. وكان نموذج بور معتمدا على التصور الكمومي للزخم الزاوي (أي تكون له قيم خاصة ذاتية):
وطبقا ل «دي برولي» يوصف الإلكترون بموجة ذات عدد صحيح من طول الموجة، وأنه في الذرة لا بد وأن يناسب العدد الموجي محيط مدار الإلكترون:
ولكن هذا الافتراض يحصر موجة الإلكترون في بُعد واحد ويدور في مدار دائري.
وابتداء من تلك الافتراضات علّق الفيزيائي بيتر ديباي بأنه إذا كان الجسيمات تتصرف بخصائص الموجات فلا بد لها أن تفي بنوع من أنواع دالة موجية. ومن ذلك التعليق الذي قدمه «ديباي» حاول شرودنجر التوصل إلى معادلة موجية في ثلاثة أبعاد تنطبق على الإلكترون. واستعان بما قام به هاميلتون من بيان التناظر بين ميكانيكا الأجسام وخواص الضوء والذي يتمثل في المشاهدة أن الحد الصفري لطول الموجة (أي عندما يصل طول الموجة إلى 0) يعادل حالة نظام في الميكانيكا الكلاسيكية.[3]. وتوصل شرودنجر إلى المعادلة:[4]
تفسير ذرة الهيدروجين[عدل]
تستخدم معادلة شرودنجر ذات الثلاثة أبعاد في التطبيق على ذرة الهيدروجين:[5][6]
حيث:
- شحنة الإلكترون،
- بُعد الإلكترون عن النواة (|| =),
- الجزء الممثل للجهد هو الجهد الكهربائي، وفيه
السماحية الكهربائية في الفراغ،
والأخيرة هي الكتلة المخفضة المكونة من نواة الهيدروجين (وهي بروتون واحد) كتلتها وكتلة الإلكترون . ومعنى الإشارة السالبة، أنه يوجد تجاذب بين شحنة النواة الموجبة وشحنة الإلكترون السالبة. ونأخذ الكتلة المخفضة في الاعتبار حيث يتحرك كل من النواة والإلكترون جول مركز الثقل، فهما يكونان نظاما مكون من جسمين. وحركة الإلكترون هي التي تهمنا حيث كتاته هي الأصغر.
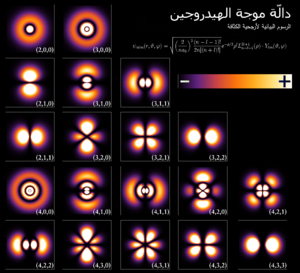
وتشكل الدالة الموجية للهيدروجين هي دالة لموقع الإلكترون ويمكن فصلها إلى ثلاثة دوال في الاتجاهات الثلاث.[7] ويتم ذلك للسهولة بتطبيق النظام الإحداثي الكروي:
حيث:
- دوال شعاعية،
- توافقية كرية من الدرجة والنوع .
وتلك هي الذرة الوحيدة التي حلت لها معادلة شرودنجر بدقة. أما بالنسبة إلى الذرات الأخرى المحتوية على أكثر من إلكترون واحد فهي تتطلب طرق تقريبية نابعة من معادلة شرودنجر. مجموعة الحلول هي:[8]
حيث:
- نصف قطر بوهر،
- كثيرة حدود لاجير العامة من الدرجة .
- عدد كم رئيسي، عدد كم مداري، وعدد كم مغناطيسي، وهم يتخذون القيم:
ينطبق هذا الحل تماماً مع قياسات طيف ذرة الهيدروجين، وكان ذلك نجاحاً عظيماً لمعادلة شرودنجر والتي أيدت طريقة ميكانيكا المصفوفات الكمية التي اتبعها هايزنبرج قبله بثلاثة سنوات عام 1923، بذلك أعتلت ميكانيكا الكم مكانتها كواحدة من أعظم النظريات الفيزيائية.
ومن الجدير بالذكر أن خلال السنوات التالية اكتشف بأن الإلكترون يدور حول محوره أي أن له عزم مغزلي، واكتشفت تلك الظاهرة من انشقاق خطوط الطيف للعناصر، فكان ذلك داعياً لإدخال عدد كم مغزلي وأكتملت الأعداد الكمية الخاصة بذرة الهيدروجين وكذلك لكافة الذرات المعروفة، وأصبحت الأعداد الكمومية كالآتي:
انظر أيضًا[عدل]
مراجع[عدل]
- ^ "Wayback Machine" (PDF). مؤرشف من الأصل في 2019-09-02. اطلع عليه بتاريخ 2019-09-05.
{{استشهاد ويب}}: صيانة الاستشهاد: BOT: original URL status unknown (link) - ^ de Broglie، L. (1925). "Recherches sur la théorie des quanta" [On the Theory of Quanta] (PDF). Annales de Physique. ج. 10 ع. 3: 22–128. مؤرشف من الأصل (PDF) في 2013-07-17. Translated version.
- ^ Schrodinger، E. (1984). Collected papers. Friedrich Vieweg und Sohn. ISBN:3-7001-0573-8. See introduction to first 1926 paper.
- ^ Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, (Verlagsgesellschaft) 3-527-26954-1, (VHC Inc.) ISBN 0-89573-752-3
- ^ Quanta: A handbook of concepts, P.W. Atkins, Oxford University Press, 1974, (ردمك 0-19-855493-1)
- ^ Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry (Volume 1), P.W. Atkins, Oxford University Press, 1977, (ردمك 0-19-855129-0)
- ^ Physics for Scientists and Engineers - with Modern Physics (6th Edition), P. A. Tipler, G. Mosca, Freeman, 2008, ISBN 0-7167-8964-7
- ^ David Griffiths (2008). Introduction to elementary particles. Wiley-VCH. ص. 162–. ISBN:978-3-527-40601-2. مؤرشف من الأصل في 2020-04-21. اطلع عليه بتاريخ 2011-06-27.
| في كومنز صور وملفات عن: معادلة شرودنغر |














































![{\displaystyle \psi _{n\ell m}(r,\theta ,\phi )={\sqrt {{\left({\frac {2}{na_{0}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n[(n+\ell )!]^{3}}}}}e^{-r/na_{0}}\left({\frac {2r}{na_{0}}}\right)^{\ell }L_{n-\ell -1}^{2\ell +1}\left({\frac {2r}{na_{0}}}\right)\cdot Y_{\ell }^{m}(\theta ,\phi )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58d5e46f4f0aa77aa1dfb77f1186590377a078c2)







