تجاوز الحد (إشارة)

في تحليل الإشارة، ونظرية التحكم، والإلكترونيات والرياضيات، تجاوز الحد هو أن تتجاوز الإشارة أو الدالة هدفها. ويزداد خصوصا في استجابات الأنظمة ذات النطاقات المحدودة مثل مرشح الترددات المنخفضة. وغالبا يتبعها حدوث رنين، حيث تقترن في نفس الوقت معه.
التعريف[عدل]

تم تعريف أقصى تجاوز للحد في أنظمة التحكم المنفصلة زمنيا لكاتسوهيكو أوجاتا على أنها أقصى قيمة عظمى لمنحنى الاستجابة وتقاس من الاستجابة المطلوبة للنظام.[1]
نظرية التحكم[عدل]
في نظرية التحكم، يشير تجاوز الحد إلى الخرج الذي يتجاوز آخر قيمة ثابتة.[2] وبالنسبة إلى دخل الدالة، فإن تجاوز الحد المئوي (PO) هو حاصل طرح أقصى قيمة من قيمة الدالة ومقسوما على قيمة الدالة. وفي حالة دالة الوحدة، فإن تجاوز الحد هو حاصل طرح أقصى قيمة لإستجابة الدالة من واحد.
تجاوز الحد المئوي هو دالة في نسبة الإخماد (ζ) ويعطى بالعلاقة:[3]
ويمكن إيجاد نسبة الإخماد أيضا عن طريق:
الإلكترونيات[عدل]
في الإلكترونيات، تجاوز الحد يشير إلى القيم العابرة لأي عنصر يتجاوز قيمته النهائية عند انتقاله من قيمة لأخرى. ومن التطبيقات الهامة لتجاوز الحد هو إشارة الخرج للمضخم.[4]
توضيح: يحدث تجاوز الحد عندما تتجاوز القيم العابرة لقيمها النهائية. وعندما تكون أقل من القيمة النهائية فإن هذه الظاهرة يطلق عليها «تحت الحد».
تصمم الدائرة لتقليل زمن الارتفاع عندما تحتوي على تشوه للإشارة في حدود مسموح بها.
- تجاوز الحد يشير إلى تشوه الإشارة.
- أثناء تصميم الدائرة، يمكن أن تتداخل أهداف تقليل تجاوز الحد وتقليل زمن الارتفاع.
- تعتمد قيمة تجاوز الحد على الفترة الزمنية لظاهرة تسمى «التخميد».
- يتعلق تجاوز الحد غالبا بزمن الاستقرار، وهو المدة الزمنية التي يأخذها الخرج للوصول إلى حالة الاستقرار.
الرياضيات[عدل]
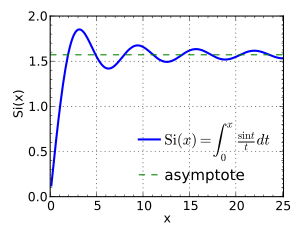
أثناء تقريب الدوال، يعتبر تجاوز الحد أحد العناصر التي تصف جودة التقريب. عندما تكون دالة مثل موجة مربعة ممثلة بمجموع عدد من الحدود، على سبيل المثال، متسلسلة فورييه أو متعددة حدود متعامدة. تقريب الدالة بواسطة مجموعة من الحدود في المتسلسلة يمكن أن يؤدي إلى منع تجاوز الحد، تحت الحد والرنين. وكلما زادت حدود المتسلسلة، كلما كان التقريب أوضح وأسهل في الدالة. وعلى الرغم من تقليل المدة الزمنية للتذبذبات، فإن سعة النطاق لا تقل.[5] وهذا يطلق عليه ظاهرة جيبس. وفي تحويل فورييه، فإنه يمكن نمذجته بتقريب دالة الوحدة لعدد صحيح من الترددات الحقيقية. ويمكن تفسير ذلك على أنه التفاف حول دالة السينك (sinc) أثناء معالجة الإشارات، وهذا يطلق عليه مرشح ترددات منخفضة.

معالجة الإشارة[عدل]
أثناء معالجة الإشارة، تجاوز الحد يحدث عندما يحتوي خرج المرشح على قيمة أعلى من دخله، خصوصا في استجابة الدالة، وكثيرا ما ينتج ظاهرة ذات الصلة بالرنين.
يحدث هذا على سبيل المثال عند استخدام مرشح سينك كمرشح ترددات منخفضة مثالي. ويمكن تفسير استجابة الخطوة على أنها الالتفاف بالإستجابة النبضية والتي تعتبر دالة سينك.
يمكن فهم حد التجاوز وتحت الحد بهذه الطريقة: يتم تنظيم الدوال غالبا لكي تحتوي على عدد صحيح، ولذلك فإنه يتم إرسال دوال ثابتة لأهداف ثابتة، كما أنها تحتوي على كسب كهربائي. قيمة الالتفاف حول نقطة معينة لإشارة الدخل، بمعاملات (أوزان) قيم الدوال. إذا كانت الدالة غير سالبة كما في الدالة الغاوسية، فإن قيمة الدالة سوف تكون مجموعة من قيم الدخل (المعاملات الصحيحة والتي تساوي 1، كما أنها ليست سالبة)، وهذا يؤدي إلى وقوعها بين أقل قيمة وأقصى قيمة لإشارة الدخل. كما أنها لن تكون تجاوز الحد أو تحت الحد، إذا تم فرض الدوال بقيم سالبة، كما في دالة سينك، وبالتالي فإن قيمة الإشارة سوف تكون تركيب أفيني من قيم الدخل، ويمكن وقوعها خارج أقل قيمة وأقصى قيمة لإشارة الدخل، متسببا في تجاوز الحد وتحت الحد.
تجاوز الحد غالبا يكون غير مرغوب به، خاصة أنه يسبب تشوه، ولكنه يكون أحيانا مطلوب أثناء شحذ الصورة، بسبب زيادة حدة الصورة.

المفاهيم المتعلقة[عدل]
الظاهرة المتعلقة بتجاوز الحد هي الرنين، وتهبط الإشارة تحت قيمة الاستقرار، ومن الممكن أن ترتفع مرة أخرى، حيث تأخذ بعض الوقت للوصول إلى قيمة الاستقرار، ويطلق على هذا الزمن زمن الاستقرار.
في علم البيئة، تجاوز الحد هو مفهوم نظري، حيث يتجاوز عدد السكان السعة المقدرة للنظام.

انظر أيضا[عدل]
المصادر[عدل]
- ^ Ogata، Katsuhiko (1987). Discrete-time control systems. Prentice-Hall. ص. 344. ISBN:0-13-216102-8.
- ^ Kuo, Benjamin C & Golnaraghi M F (2003). Automatic control systems (ط. Eighth). NY: Wiley. ص. §7.3 p. 236–237. ISBN:0-471-13476-7. مؤرشف من الأصل في 2019-12-14.
- ^ Modern Control Engineering (3rd Edition), Katsuhiko Ogata, page 153.
- ^ Phillip E Allen & Holberg D R (2002). CMOS analog circuit design (ط. Second). NY: Oxford University Press. Appendix C2, p. 771. ISBN:0-19-511644-5. مؤرشف من الأصل في 2019-12-14.
- ^ Gerald B Folland (1992). Fourier analysis and its application. Pacific Grove, Calif.: Wadsworth: Brooks/Cole. ص. 60–61. ISBN:0-534-17094-3. مؤرشف من الأصل في 2019-12-14.


