موجة صادمة

الموجة الصادمة[1] أو الموجة الصدمية[2] أو موجة الصدمة تتكون عند تحرك جسم بين طبقات الهواء بنفس سرعة الموجات الصوتية الناتجة أو بسرعة أكبر. وهي كالاضطراب في الهواء أو فرقعة. و بصفة أعم تنتج موجة الصدمة عند تحرك جسم ما في مائع بسرعة تفوق سرعة إظطرابات أو اهتزازات المائع. فمثلا سرعة اهتزازات الهواء، المعروفة بسرعة الصوت، تبلغ حوالي 340 م/ث، فإذا انطلقت طائرة أو رصاصة بسرعة تفوق 340 م/ث ظهرت موجة صدمة. وكذلك تبلغ سرعة اهتزازات داخل الماء حوالي 1500 م/ث. وتبلغ سرعة اهتزازات على سطح الماء أقل من 1 م/ث، فإدا انطلقت باخرة بسرعة أكبر رأينا موجة، مرتفعة على سطح الماء، تبدأ من مقدمتها مشكلة، إلى الوراء، زاوية كانت حادة كلما كانت السرعة أكبر.
تشبه الموجة العادية، ولكنها تحمل طاقة مركزة وتنتشر خلال وسط (صلب أو سائل أو غاز) أو أحيانا خلال حقل فيزيائي كالمجال الكهرومغناطيسي. وتتميز تلك الموجة الاصطدامية بعنصر قصر زمن حدوثها، وبتغيير متقطع في خصائص الوسط المحيط. وتتسبب الموجة التصادمية في ارتفاع سريع وهائل في الضغط و درجة الحرارة والكثافة في الوسط . تنتقل الموجة التصادمية خلال الوسط المحيط بسرعة أعلى بكثير من الموجة العادية. تتلاشى طاقة موجة الصدمة بسرعة بالتناسب مع المسافة ، فالموجة المصاحبة المتمددة ستندمج مع تلك الموجة مما يعني إلغاء جزئيا لها. بالتالي فإن الانفجار الصوتي المرتبط مع مرور طائرة فوق صوتية يكون هو موجة الصوت الناتجة من تدهور واندماج موجة الصدمة مع الموجة المتمددة الناشئة بواسطة الطائرة.
عند مرور موجة الصدمة خلال المادة، فإن إجمالي الطاقة لا تتبدد، ولكن الطاقة التي تستخرج كشغل ستتبدد والاعتلاج سيزداد. وهذا مما يزيد من قوة السحب الإضافية على الطائرة عند حصول تلك الموجة.
المصطلحات[عدل]

تنقسم موجة الصدمة إلى قسمين:
- طبيعية: تكون 90 درجة عمودية على اتجاه تيارالمار على الوسط.
- مائلة: تأخذ زاوية مائلة مع اتجاه التيار.
هناك أشكال أخرى من موجة الصدمة:
- جبهة الصدمة Shock Front: وهو الاسم البديل للموجة الصدمية
- جبهة الاتصال Contact Front: بالموجة الصدمة تكون بسبب تأثير صدمة ما (بما فيها تأثير الصدمة من الارتفاع الهائل والسريع لضغط تيار الهواء). فموقع تأثير الصدمة يتبع جبهة الاتصال بجبهة الصدمة.
التيارات فوق الصوتية[عدل]

عندما يمر جسم ما بسرعة أعلى من المعلومات المعطاة حول انتشارها خلال محيط المائع، فإن المائع القريب من الاضطراب لايتمكن من التفاعل أو الابتعاد قبل وصول الاضطراب إليه. تتغير خاصية المائع (الكثافة، الضغط، الحرارة، السرعة، رقم الماخ) بشكل فوري عند حضور موجة الصدمة. قيمة قياسات سماكة موجة الصدمة قد تعادل واحد قيمة أسية أكثر من متوسط مسار الهواء الحر الخاضع للفحص.
تتشكل موجة الصدمة عندما يكون الهواء سرعته أعلى من سرعة الصوت.[3] وبالنطاق الذي يحصل ذلك فإن موجات الصوت تسير عكس التيار لتصل للنقطة التي لا يمكن ان تتخطاها مما يجعل الضغط يتراكم بسرعة عند تلك النقطة وبسرعة ستتكون موجة الصدمة ذات الضغط الهائل. موجات الصدمة هي ليست موجات صوتية تقليدية، فهي تتشكل بلحظة اختلاف عنيفة جدا لخصائص الغازات وبناء على أوامر من متوسط المسارات الحرة (تقريبا ميكرو-متر بالحالات الجوية) من السماكة. لذلك ستسمع موجات الصدمة كدوي فرقعة قوية أو قصف. ستنتقل موجة الصدمة من موجة مائلة إلى موجة مستقيمة خلال مسافات طويلة، متحولة إلى موجة الصوت التقليدية حيث أنها ستسخن الهواء مما يفقدها الطاقة. تلك الموجة الصوتية ستسمع كأنها انفجار مكتوم أو صوت عال لحاجز الصوت، وهي ناتجة بشكل عام من تجاوز سرعة الطائرة سرعة الصوت.
موجة الصدمة هي إحدى صور ضغط الهواء بحالة مرور تيار فوق صوتي. بعض الحالات الأخرى هي التيار متساوي الاعتلاج الحراري (isentropic compressions)، إضافة لضغوط براندت- ماير. تنتج طريقة الضغط للغاز كثافة وحرارة مختلفين عن المعدل المعطى للضغط.
موجة الصدمة العادية[عدل]
بإمكان موجة الصدمة ان تتشكل من خلال انحدار شديد للموجات العادية. وأفضل مثال لتلك الظاهرة هي موجات المحيط التي تتكسر بقوة على الشاطئ. بالمياه غير العميقة تعتمد سرعة موجات السطح على مدى عمق المياه. لذلك تكون قمة موجات المحيط هي أسرع قليلا من المنخفض ما بين الموجتين، وذلك بسبب ان ارتفاع الموجة ليست صغيرة جدا مقارنة مع عمق الماء. فقمة الموجات ستتجاوز المنخفض حتى تكون مقدمة الموجة تشكلت عموديا وانتشرت على صورة صدمة مضطربة أو موجة تتكسر على الصخر وستبدد طاقة الموجة على شكل صوت وحرارة.
ظاهرة شبيهة تؤثر على الموجات الصوتية القوية بالغاز أو البلازما، ذلك بسبب اعتماد موجة الصوت على الحرارة والضغط. فالموجات القوية تسخن الوسط المحيط القريب من جبهة الضغط. وخلال انضغاط كظمي (adiabatic compression) للهواء نفسه، فالجبهات الضغط العالية تتجاوز المنخفضة المجاورة لها. فتشكيل الصدمة بواسطة تلك العملية لا تحصل لموجات الصوت بالغلاف الجوي للأرض، ولكن يعتقد بانها إحدى الميكانيكيات التي تسخن غلاف اللون الشمسي (solar chromosphere) والهالة المحيطة بها (Corona) حيث تنتشر الموجات داخل محيط الشمس.
إذا كان التدفق قابلاً للانضغاظ في مسار قليل الانحرافات، فان التدفق عكسوي والانتروبيا ثابته. لكن إذا كان التدفق سريع وسرعته تفوق سرعة الصوت وفي نفس الوقت يوجد تغير مفاجئ في مساحة مسار التدفق، فان التدفق في هذه الحالة يصبح غير عكسوي والانتروبيا في ازدياد. بشكل عام، موجة الصدمة تتكون حينما تتغير خصائص الغاز بمقدار كبير ومفاجئ. خلال موجة الصدمة فإن الضغط الساكن والحرارة وكثافة الغاز تزداد لحظياً. موجة الصدمة لا تضيف أو تستهلك شغل فلذلك لن يكون هناك أي تبادل حراري وأيضا لهذا السبب فان الاثلبيا والحرارة ثابتين. لكن، عملية موجة الصدمة ليست عملية متساوية الانتروبية، فلذلك مجموع الضغط في اتجاه التيار دائماً اقل من مجموع الضغط عكس التيار ويفسر تلك الخسارة في الضعط، ان موجة الصدمة تساهم في خسارة الضغط. التغيير في مجموع الضغط أثناء موجة الصدمة يجعل معادلة بيرنولي غير صالحة وفي نفس الوقت رقم ماخ وسرعة التدفق تقل أيضا.
إذا كانت موجة الصدمة عامودية على اتجاه مسار التدفق فان هذه الظاهرة تسمى موجة الصدمة العادية. وفي الأسفل مجموعة من المعادلات التي تفسر متغيرات التدفق أثناء موجة الصدمة العادية. المعادلات الآتية اُسْتُنْتِجَت من قانون حفظ الكتلة والزخم والطاقة.
أثناء عملية موجة الصدمة العادية فان رقم ماخ يقل ويمكن تفسير ذلك من خلال هذه المعادلة:
M1^2 = [(gam - 1) * M^2 + 2] / [2 * gam * M^2 - (gam - 1)]
درجة الحرارة لا تتغير خلال موجة الصدمة العادية
Tt1 / Tt0 = 1
درجة الحرارة الساكنة تزداد:
T1 / T0 = [2 * gam * M^2 - (gam - 1)] * [(gam - 1) * M^2 + 2] / [(gam + 1)^2 * M^2]
الضغط الساكن يزاداد:
p1 / p0 = [2* gam * M^2 - (gam - 1)] / (gam + 1)
الكثافة تتغير:
r1 / r0 = [(gam + 1) * M^2 ] / [(gam -1) * M^2 + 2]
مجموع الضعط يتغير إلى:
pt1 / pt0 = {[(gam + 1) * M^2 ] / [(gam - 1) *M^2 + 2]}^[gam/(gam-1)] * {(gam + 1) /[2 * gam * M^2 - (gam - 1)]}^[1/(gam - 1)]
الجزء الأيمن لكل المعادلات السابقة يعتمد على رقم ماخ. يمكن التعرف على جميع الظروف والحالات المتعلقة بموجة الصدمة العادية إذا كان رقم ماخ متاح.
النظائر[عدل]
يمكن وصف موجة الصدمة بأنها أبعد نقطة معاكسة لجسم متحرك والذي يعرف عن وصول الجسم. وتعرف موجة الصدمة بأنها الغلاف ما بين نطاق ليس بها حالة وصول الصدمة ونطاق يحتوي على حالة الصدمة. النظير لذلك هو مخروط الضوء الموصوف بنظرية النسبية العامة.
بالمختصر، للحصول على الموجة الصدمية، وذلك بالمرور بسرعة أعلى من سرعة الصوت. بتلك الحالة سيكون هناك اجزاء من الهواء المحيط بالطائرة يسير بسرعة الصوت مع الطائرة، لذلك فموجات الصوت تتراكم مع بعضها البعض في محاولة لترك الطائرة وأشبه وصف لذلك هو تزاحم السيارات على الطريق، عند تلك اللحظة تنشئ موجة الصدمة ويرتفع الضغط بسرعة شديدة فتتشتت على جانبي الطائرة. وبسبب ذلك التضخيم تكون موجة الصدمة شديدة جدا، اشبه بالانفجار عند سماعه. الظاهرة النظيرة هي خارج ميكانيكية الموائع. مثال الجزيئات المتسارعة فوق سرعة الضوء بوسط منكسر (حيث سرعة الضوء بوسط هي أقل بالماء من الفراغ) ستنتج تأثير صدمة ضوئية، وتسمى تلك الظاهرة بإشعاع شيرنكوف (Cherenkov radiation).
الأمثلة[عدل]
سنري مجموعة من الأمثلة من الموجات الصدمية، مجتمعة مع ظواهر صدمية مشابهة:
صدمات متحركة[عدل]
- تحتوي عادة على موجات صدمية تنتشر داخل وسط ثابت غير متحرك.
- بتلك الحالات، فأن الهواء بمقدمة الصدمة يكون ثابت والغاز الذي خلف الصدمة يكون فوق صوتي (عادة يكون في اطار المختبرات). فالصدمة تنتشر مع مقدمة موجة عادية (وتكون عمودية عليها) باتجاه التيار. تستخلص سرعة الصدمة من معدل الضغط الرئيسي ما بين جسمين غازيين.
- تتكون الموجات الصدمية بتفاعل ما بين جسمين غازيين مختلفين بالضغط، حيث تتمدد موجة الصدمة داخل الغاز الأقل كثافة وموجة التمدد تنتشر داخل الغاز الأعلى ضغط.
- مثال على ذلك: انفجار البالون، موجة الصدمة ناشئة من انفجار، الإنبوب الصدمي.
موجة تفجيرية[عدل]
الموجة التفجيرية أو انفجار صاعق هي موجة صدمية مدعمة بتفاعل من الحرارة الخارجية الطاردة. وهي موجة تمر بوسط احتراق عالي أو وسط كيميائي مضطرب، كانفجار أو تفاعل اوكسجين مع ميثان. فالتفاعل الكيميائي داخل الوسط ينتج بعد حدوث موجة الصدمة فتحرك الطاقة الكيميائية الناتجة من التفاعل الموجة للخارج.
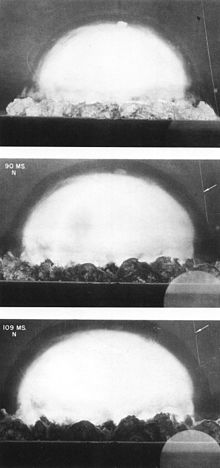
- الموجة التفجيرية تنتج باختلاف بسيط عن الموجة العادية حيث أنها تقاد بواسطة تفاعل كيميائي يحصل بعد مواجهة الموجة الصدمية. ويسبب الانفجار أيضا صدمة من النوع الأول بالصورة فوق، تنتشر داخل الجو المحيط وذلك خلال الضغط المفرط الناتج من الانفجار.
صدمة منفصلة[عدل]

تلك الموجات تكون منحنية وتنشئ امام الجسم بمسافة بسيطة، وتكون 90 درجة امام الجسم مباشرة ومن ثم تنحني حول الجسم. الصدمات المنفصلة لها نفس الحسابات التحليلية كالتي بالصدمات المتلاصقة، التيار القريب من تلك الموجة لهاموضوع ذو اهتمام متواصل بسبب القواعد التي تحكم مسافة الصدمة في مقدمة جسم مثلوم تكون معقدة، وهي خاصية لشكل الجسم، بالإضافة فالمسافة المتعادلة للصدمة تختلف بشدة حسب الحرارة عند الغازات غير الخاملة، مسببة باختلاف كبير بتحويل الحرارة إلى نظام الوقاية الحرارية عند المركبة
- مثل تلك الصدمة تحصل عندما تتجاوز زاوية انحراف القصوى. وترى تلك الصدمات المنفصلة على أجسام غير حادة الطرف أو المثلومة، ولكن يمكن رؤيتها على الأجسام الحادة بسرعات منخفضة لرقم الماخ.
- امثلة: المركبات الفضائية العائدة (أبوللو والأتوبيس الفضائي)، الطلقات النارية، حاجز طبقة المغناطيسية للشمس
صدمة متصلة[عدل]
- تلك الصدمات تظهر كموجات متصلة على طرف الحاد لجسم يتحرك بسرعات فوق صوتية
- أمثلة: الأوتاد والمخاريط فوق الصوتية مع زوايا الذروة الصغيرة
- موجات الصدمة المتصلة هي بناء تقليدي مبسط بالتحريك الهوائي بسبب، الغاز المثالي ومجال تيار غير مائع وتوفر تحليل للمحلول كمعدل الضغط والحرارة وزاوية الوتد ورقم الماخ المصرف وستحسب جميعا مما يعطي رقم الماخ النبع وزاوية الصدمة. زوايا الصدمة الصغيرة ترتبط مع الأرقام الكبيرة لماخ المنبع، وبالحالة الخاصة عندما تكون موجة الصدمة 90 درجة على التيار الخارج (صدمة عادية) وهي مرتبطة مع رقم 1 ماخ.
تعريف آخر[عدل]
لا ينحصر اصطلاح الموجة الاصتدامية فقط في الطيران، بل تستخدم أيضا لوصف ظواهر طبيعية مثل الانفجار الذي يحدثة أحد النيازك عند اصتدامه بحو الأرض، مثلما حدث في انفجار تونغوسكا بسيبيريا عام 1908 أو حادثة سقوط النيزك في روسيا 2013. كذلك نجد الموجات الاصتدامية في حالة انفجار مستعر أعظم مما يشاهد في أمثلة عديدة في الكون .
انظر أيضا[عدل]
- رقم ماخ الحرج
- موجة الصدمة العادية
- طيران بسرعة عالية
- انفجار صاعق
- مجال شمسي
المصادر[عدل]
- ^ الشرق الأوسط[وصلة مكسورة] نسخة محفوظة 14 أبريل 2020 على موقع واي باك مشين.
- ^ الأهرام نسخة محفوظة 17 ديسمبر 2014 على موقع واي باك مشين.
- ^ Settles, Gary S. (2006), High-speed Imaging of Shock Wave, Explosions and Gunshots, vol. 94, American Scientist, pp. pp. 22-31
وصلات خارجية[عدل]
- تقدير قنبلة موجة الصدمة
- معلومات من مركز أبحاث جلين بناسا عن:
- أساسيات التيار المضغوط, 2007
| في كومنز صور وملفات عن: موجة صادمة |
