لعبة الحياة (حوسبة)
هذه المقالة عن لعبة رياضية تمثل خلايا ذاتية السلوك. لمعانٍ أخرى، طالع لعبة الحياة (توضيح).
لعبة الحياة لكونواي أو لعبة الحياة (بالإنجليزية: Game of Life) هي خلايا ذاتية السلوك تم اختراعها من قبل عالم الرياضيات البريطاني جون هورتون كونواي في عام 1970.[1]
لعبة الحياة هي لعبة بدون لاعبين، مما يعني أن تطورها يتحدد بحالتها الأولية، ولا يتطلب أي مزيد من المدخلات. من الممكن لأحد أن يتفاعل مع لعبة الحياة بإنشاء تكوين أولي ومراقبة كيف له أن يتطور.
قواعد
لعبة الحياة العامة هي شبكة ثنائية الأبعاد لانهائية الحجم على شكل خلايا مربعة، كل من الخلايا يكون في واحدة من الحالتين الممكنتين، حية أو ميتة. تتفاعل كل خلية مع ثمانية من الخلايا المجاورة لها أفقياً ورأسيا وقطرياً. في كل لحظة من الوقت تحدث التحولات التالية:
- تموت أي خلية حية لها أقل من اثنتين من الجيران الأحياء.
- أي خلية حية لها اثنتين أو ثلاثة جيران من الخلايا الحية تعيش إلى الجيل القادم.
- تموت أي خلية حية لها أكثر من ثلاثة جيران من الخلايا الحية.
- أية خلية ميتة تصبح حية عندما يصبح حولها بالضبط ثلاثة من الخلايا الأحياء.
يشكل النمط الأولي ما يعرف باسم بذور النظام. ويتم إنشاء الجيل الأول بواسطة تطبيق القواعد المذكورة أعلاه في نفس الوقت لكل خلية في البذور. تحدث الولادات والوفيات في وقت واحد. يستمر تطبيق القواعد بشكل مستمر لتوليد الأجيال اللاحقة.
أمثلة لأنماط شهيرة
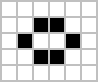
تم اكتشاف الأنماط الأولى المثيرة للاهتمام في لعبة الحياة دون استخدام أجهزة الكمبيوتر. من أبسط الأنماط الثابتة هي «الحياة الثابتة» و«المذبذبات».
|
|
| ||||||||||||||||||||||||||
تقوم المركبات الفضائية بالتفاعل مع باقي اللعبة بطرق مثيرة للاهتمام: فعند ضبط الزوايا والتوقيت يمكن نقل مربع بوسط طائرتين شراعيتين. حيث يساهمان في تدمير القديم وإنشاءه من جديد في موضع أقرب لمصدر الطائرتين. وباستخدام ثلاث طائرات شراعية ينقل في الاتجاه المعاكس. يمكن استخدام ذلك كعداد كما يمكن استخدام الطائرات الشرعية في تكوين البوابات المنطقية الأساسية مثل AND وOR وNOT. يمكن استخدام هذه المكونات في بناء آلة ذات حالات منتهية متصلة بعدادين والتي تكافئ آلة تورنغ عمومية (أي لديها القدرة على محاكاة أي آلة تورنغ). يعني ذلك أن لعبة الحياة نظريا لها نفس القدرة الحسابية التي يتمتع بها حاسوب ذو ذاكرة لا نهائية ويعمل لوقت غير محدود: أي أنها كاملة حسب تورنغ.
مراجع
- ^ Gardner، Martin (1970-10). Mathematical Games - The fantastic combinations of John Conway's new solitaire game "life". ج. 223. ص. 120–123. مؤرشف من الأصل في 2009-06-03. اطلع عليه بتاريخ 2011-06-26.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ=(مساعدة) و|عمل=تُجوهل (مساعدة)صيانة الاستشهاد: التاريخ والسنة (link)
وصلات خارجية
- لعبة الحياة (حوسبة) على مشروع الدليل المفتوح
- أخبار لعبة الحياة
- ويكي لعبة الحياة
- أسئلة متكررة عن لعبة الحياة
