مدار جزيئي: الفرق بين النسختين

تصفح التاريخ تفاعلياً

[نسخة منشورة]

→ التعديل السابق التعديل اللاحق ←

تم حذف المحتوى تمت إضافة المحتوى

مرئينص الويكي

مضمن

نسخة 06:41، 13 فبراير 2014

المدار الجزيئي هو دالة رياضية تصف السلوك الموجي للإلكترون في جزيء ما. .^[1] يمكن استخدام هذه الدالة لحساب وتحديد الخصائص الفيزيائية والكيميائية للجزيء، كما يمكن بواسطتها تععين احتمالية وجود إلكترون في منطقة ما حول الذرات المكونة للجزيء.

نظرة عامة

كلمة مدار ابتدعها الكيميائي روبرت موليكن أثناء ترجمته لمصطلح 'Eigenfunktion' الذي استعمله إرفين شرودنغر خلال أبحاثه في ميكانيكا الكم.

تشكيل المدارات الجزيئية

تنشأ المدارات الجزيئية من التفاعلات المسموح بها باندماج المدارات الذرية بحيث تحصل عملية تهجين لهذه المدارات. (تحدد من نظرية الجماعة) للمدارات الذرية المتوافقة مع بعضها البعض. يتم تحديد كفاءة التفاعلات المدارية الذرية من التداخل المداري (وهو مقياس لمدى نجاح اثنين من مدارات التفاعل البناء مع بعضها البعض) بين اثنين من المدارات الذرية، وهو أمر مهم إذا كان المدارات الذرية هي قريبة في الطاقة.

المدارات الجزيئية تعطى الأسماء (سيجما , باي ، دلتا ) وقد يكون التداخل بناء ، أو غير بناء وفي هذه الحالة توضع علامة «*» على رمز السيجما والمدارات الجزيئية سيجما هي تلك الناتجة عن إحدى التداخلات التالية:

تداخل المدار الذري (s ) معمدار ذري آخر (s )
تداخل المدار الذري (s) مع مدار ذري (p )
تداخل المدار الذري (p ) مع مدار ذري آخر (p)

أولاً : المدارات الجزيئية (سيجما) الناتجة عن تداخل مدارين ذريين من نوع ( s ):

مناقشة نوعية

مزيج خطي للمدارات الذرية (LCAO)

المصادر

^ Mulliken، Robert S. (يوليو 1932). "Electronic Structures of Polyatomic Molecules and Valence. II. General Considerations". Physical Review. ج. 41 ع. 1: 49–71. Bibcode:1932PhRv...41...49M. DOI:10.1103/PhysRev.41.49.

وصلات خارجية

Java molecular orbital viewer shows orbitals of hydrogen molecular ion.
The orbitron, a visualization of all atomic, and some molecular and hybrid orbitals
xeo Visualizations of some atomic and molecular atoms
Simulations of molecules with electrons caught in molecular orbital (Simulations run on PC only.)
OrbiMol Molecular orbital database.

هذه بذرة مقالة عن الكيمياء بحاجة للتوسيع. فضلًا شارك في تحريرها.

[1] Mulliken، Robert S. (يوليو 1932). "Electronic Structures of Polyatomic Molecules and Valence. II. General Considerations". Physical Review. ج. 41 ع. 1: 49–71. Bibcode:1932PhRv...41...49M. DOI:10.1103/PhysRev.41.49.

[1]

@@ سطر 1: / سطر 1: @@
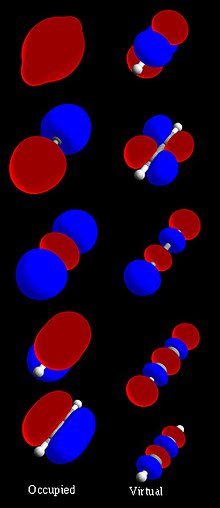
+[[File:Orbitals acetylene.jpg|left|thumb|استكمال مجموعة المدار الجزيئي لل[[اسيتيلين]] (H-C ≡ C-H) . العمود الأيسر يظهر المدارات الجزيئية (MO) التي امتلئت في الحالة الارضية، مع طاقة مدارية أدنى في الأعلى. الخط الأبيض والرمادي يوضح بعض الMO محورية جزيئية تمر بالنوى. في المناطق الحمراء موجة مدارية وظيفية موجبة والسالبة في الزرقاء. العمود الأيمن يظهر  MO الظاهرية التي هي فارغة في الحالة الارضية، ولكن ممتلئة  عند حالة الاثارة.]]
 [[ملف:Dihydrogen-HOMO-phase-3D-balls.svg|تصغير|مدار جزيئي من النمط σ لجزيء الهيدروجين]]
 '''المدار الجزيئي''' هو [[دالة رياضية]] تصف السلوك الموجي [[إلكترون|للإلكترون]] في [[جزيء]] ما.
+.<ref>{{cite journal
+ | last=Mulliken | first=Robert S.
+ | title=Electronic Structures of Polyatomic Molecules and Valence. II. General Considerations
+ |date=July 1932
+ | journal=[[Physical Review]]
+ | volume=41 | issue=1 | pages=49–71
+ | bibcode = 1932PhRv...41...49M
+ | doi = 10.1103/PhysRev.41.49
+}}</ref>
+يمكن استخدام هذه [[الدالة]] ل[[حساب]] وتحديد الخصائص الفيزيائية والكيميائية لل[[جزيء]]، كما يمكن بواسطتها تععين احتمالية وجود إلكترون في منطقة ما حول [[ذرة|الذرات]] المكونة لل[[جزيء]].
+== نظرة عامة ==
-يمكن استخدام هذه الدالة لحساب وتحديد الخصائص الفيزيائية والكيميائية للجزيء، كما يمكن بواسطتها تععين احتمالية وجود إلكترون في منطقة ما حول [[ذرة|الذرات]] المكونة للجزيء.
 كلمة مدار ابتدعها الكيميائي [[روبرت موليكن]] أثناء ترجمته لمصطلح 'Eigenfunktion' الذي استعمله [[إرفين شرودنغر]] خلال أبحاثه في [[ميكانيكا الكم]].
-تنشأ المدارات الجزيئية من اندماج [[مدار ذري|المدارات الذرية]] بحيث تحصل عملية [[تهجين (كيمياء)|تهجين]] لهذه المدارات.
+== تشكيل المدارات الجزيئية ==
+تنشأ المدارات الجزيئية من التفاعلات المسموح بها باندماج [[مدار ذري|المدارات الذرية]] بحيث تحصل عملية [[تهجين (كيمياء)|تهجين]] لهذه المدارات.
+(تحدد من [[نظرية الجماعة]]) للمدارات الذرية المتوافقة مع بعضها البعض. يتم تحديد كفاءة التفاعلات المدارية الذرية من التداخل المداري (وهو مقياس لمدى نجاح اثنين من مدارات التفاعل البناء مع بعضها البعض) بين اثنين من المدارات الذرية، وهو أمر مهم إذا كان [[المدارات الذرية]] هي قريبة في ال[[طاقة]].
+المدارات الجزيئية تعطى الأسماء (سيجما , باي ، دلتا )
+وقد يكون التداخل بناء ، أو غير بناء وفي هذه الحالة توضع علامة «*» على رمز السيجما
+والمدارات الجزيئية سيجما هي تلك الناتجة عن إحدى التداخلات التالية:
+*تداخل [[المدار الذري]] (s ) مع[[ مدار ذري]] آخر (s )
+*تداخل [[المدار الذري]] (s) مع [[مدار ذري]] (p )
+*تداخل [[المدار الذري]] (p ) مع [[مدار ذري]] آخر (p)
+أولاً : المدارات الجزيئية (سيجما) الناتجة عن تداخل مدارين ذريين من نوع ( s ):
+== مناقشة نوعية ==
+{{...}}
+=== مزيج خطي للمدارات الذرية (LCAO) ===
+{{...}}
+== المصادر ==
+{{مراجع}}
+== وصلات خارجية ==
+*[http://www.falstad.com/qmmo/ Java molecular orbital viewer] shows orbitals of hydrogen molecular ion.
+*[http://winter.group.shef.ac.uk/orbitron/ The orbitron], a visualization of all atomic, and some molecular and hybrid orbitals
+*[http://sourceforge.net/projects/xeo/ xeo] Visualizations of some atomic and molecular atoms
+*[http://www.webreader.net/animations.htm Simulations of molecules with electrons caught in molecular orbital] (Simulations run on PC only.)
+*[http://www.lct.jussieu.fr/pagesperso/orbimol OrbiMol] Molecular orbital database.
 {{بذرة كيمياء}}