تناظر (هندسة وصفية)
لمعانٍ أخرى، طالع تناظر (توضيح).
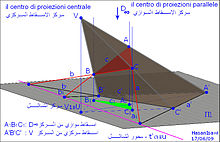
التناظر (homology ) في الهندسة الوصفية هو تحول هندسي بين شكلين متحدي المستوى (coplanar) يتم الحصول عليهما كإسقاطين لنفس الشكل.[1] بوضوح أكثر، هي العلاقة الهندسية الناشئة من إسقاط شكل ABC ينتمي على مستوى α (ألفا)، من مركزين منفصلين ∞V D، على مستوى آخر P1 (بي كريكو). العلاقة التماثلية التي تنتج بين الإسقاطين (A1B1C1) و('C'B'A) تكمن في الحصول
- على نقاط ('A1-A') (B1-B') (C-C) مصطفة مع نفس النقطة U (تسمى مركز التناظر)
- وعلى خطوط ('c1-c') (b1-b') (a1-a) تتقابل على نفس الخط u الذي يسمى محور التناظر.
وبما أن التناظر هي علاقة تقابلية بين إسقاطين لنفس الشكل دلتا على نفس المستوى. فعندما يكونان مركزي الاسقاط ، V و W ، نقطتان لانهائيتان ، فإن مركز التقابل U يكون لانهائي. الذي يمكن أن يكون عمودي على محور التقابل (u) ، عندما يحددان المركزين V و W مستوى عمودي على مستوى دلتا. وفي هذه الحالة الاخيرة التناظر يسمى تناظر عمودي[2]
حالات خاصة من التناظر[عدل]
- إذا كان هناك توازي بين المستوى α ومستوى التناظر π1، التناظر يسمى تشابه.
في هذا النوع، محور التماثل u هو خط لا نهائي، ويترتب على ذلك تشابه بين الأشكال المتناظرة.
- إذا كان رأس الهرم نقطه لانهائية (رسم 2), والمستويات المتماثلة α π1 متقاطعة، التناظر يسمى تآلف (affinity).
تقابل منظوري[عدل]
التماثل المنظوري (perspectivity)، يختلف عن التماثل (homology) في أن المنظورية تكمن في عملية إسقاط واحدة وليست في عملتين كما يحدث في التماثل (homology). أي في المنظورية التماثل يحدث بين الشكل (ABC) وإسقاطه ('C'B'A).
على سبيل المثال (رسم 3)، لدينا هرم له قاعدة ثلاثية A'B'C تنتمي إلى مستوى الإسقاط الأول π1 (پاي (حرف))، ورمزنا إلى رأس الهرم بالحرف V. إذا قطعنا الهرم بمستوى α (ألفا) ليس افقي، نلاحظ ان هناك تماثل منظوري بين القاعدة والمقطع 'A'B'C، حيث:
- النقاط المتماثلة 'A-A مصطفة مع مركز التماثل U، الذي في هذه الحالة يتطابق مع الرأس V
- والخطوط المتماثلة AB و'A'B يلتقون على محور التماثل u الذي يتطابق مع t`α (الأثر لأول للمستوى α).
- t`α هو خط التقاطع بين المستوين α وπ1.
حالات خاصة من التقابل المنظوري[عدل]
- إذا كانت الأشكال المتقابلة تنتمي إلى مستويات متوازية، فالتقابل يسمى تشابه (homothety). في هذا النوع، محور التقابل u هو خط لا نهائي، ويترتب على ذلك أن الخطوط المتقابلة تكون موازية لبعضها البعض، أي كل خطين متقابلان يلتقيان في نقطة لا نهائية، وبالتالي هناك تشابه بين الأشكال المتماثلة.
- إذا كان رأس الهرم نقطه لانهائية (رسم 2), والمستويات المتماثلة α π1 متقاطعة، فالتقابل يسمى علاقة تآلفية.
مراجع[عدل]
- ^ "معلومات عن تناظر (هندسة وصفية) على موقع babelnet.org". babelnet.org. مؤرشف من الأصل في 2019-12-15.
- ^ orthogonal projections and axonometry of a pyramid orthogonal to an inclined plane نسخة محفوظة 8 نوفمبر 2021 على موقع واي باك مشين.
انظر أيضا[عدل]
 | هذه بذرة مقالة عن الهندسة الرياضية بحاجة للتوسيع. فضلًا شارك في تحريرها. |