مبرهنة فان أوبيل
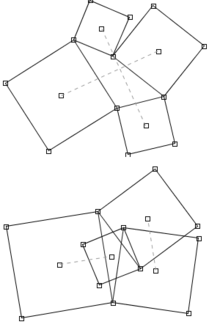
تبدأ مبرهنة فان أوبيل بإنشاء أربع مربعات على الأضلاع الأربعة لرباعي الأضلاع.[1] يتم تحديد مراكز المربعات المنشأة برسم أقطار المربعات. تنص مبرهنة فان أوبيل أن القطع المستقيمة التي تصل مركزي مربعين متقابلين تكونان متساويتين بالطول وتشكلان زاوية قائمة.
تطبق هذه المبرهنة على المضلعات الرباعية المحدبة أو المقعرة كما في الشكل.
مراجع
[عدل]- ^ Note concernant les centres de carrés construits sur les côtés d'un polygone quelconque», Nouvelle Correspondance Mathématique, vol. 4, 1878, ص. 40-44
. "نسخة مؤرشفة". مؤرشف من الأصل في 2020-03-21. اطلع عليه بتاريخ 2020-05-25.
{{استشهاد ويب}}: صيانة الاستشهاد: BOT: original URL status unknown (link)
وصلات خارجية
[عدل]
في كومنز صور وملفات عن Van Aubel's theorem.
 | هذه بذرة مقالة عن الهندسة الرياضية بحاجة للتوسيع. فضلًا شارك في تحريرها. |