فضاء الطور
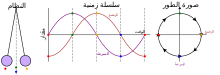
فضاء الطور أو فضاء الحالة في الفيزياء وعلم الأحياء (بالإنجليزية: Phase space) هو كمية الحالات الممكنة التي يحتويها نظام حركي.[1][2][3] وتوصف «الحالة» بواسطة مجموعة المتغيرات للنظام عند نقطة زمنية معينة. ففي الفيزياء مثلا يمكن أن تكون الحالة ممثلة بالموضع وكمية الحركة لجسيم، وبالنسبة ديناميكا حرارية تمثل دالات الحالة مثل الضغط والحجم ودرجة الحرارة مجموع تلك المتغيرات، تكون هي فضاء الحالة.
وفي علم الأحياء تعني فضاء الطور أعداد نوع الحيوانات المتنافسة. وتنتمي لكل حالة نقطة معينة في فضاء الطور، مثلما نصف كل نقطة في الفضاء بمقاييس ثلاث على 3 محاور: س، ص، ع.
أحيانا لا نكتفي بوصف جسيم بمجرد معرفة الثلاثة إحداثيات س وص وع التي تحدد وضعه وقد لا نحتاج لوصف حالته أيضا معرفة سرعته أو زخم حركته، عندئذ نلجأ إلى وصفه بفضاء الحالة أو فضاء الطور.
الاستخدام في الرياضيات[عدل]
يكون فضاء الطور فضاء رياضيا مكونا من جميع المتغيرات في نظام معين. وتشكل في أحوال كثيرة حلولا لأنظمة من المعادلات التفاضلية. ويمكن أن يتكون فضاء الطور من عدد كبير من الإحداثيات، مثلما عندما نقوم بدراسة حركات جسيمات كثيرة (مثل عدد كبير من جزيئات غاز) حيث نريد معرفتهم في لحظة معينة. فإذا اكتفينا بوصف كل جزيئ بواسطة ثلاثة إحداثيات أمكننا بيان ذلك في رسم بياني على ثلاثة محاور. ويسمى هذا «تحليل فضاء الطور».
المسقط في فضاء الطور[عدل]
تشكل جميع النقاط التي تعين تغير نظام بعد نقطة بداية المساقط في فضاء الطور. وتشكل تلك المساقط منحنيات لا تتقاطع في فضاء الطور، بحيث يمكن معرفة مسيرة كل نقطة من مسقطها. ويمكن أن تكوّن تلك المنحنيات أفلاكا كاملة (دوائر) فتصف في تلك الحالة أنظمة رنانة.
وبرغم عدم تقاطع المساقط فيمكن أن تزداد كثافتها في الفضاء أو تقل. وتعرف تلك الحالة «بكثافة فضاء الطور» ولها أهمية كبيرة في دراسة الميكانيكا الإحصائية وتمكن من إجراء حسابات دقيقة. فبالنسبة إلى تصنيف نظام حركي يهمنا معرفة تغير كثافة فضاء الطور وبالتالي حجم فضاء الطور مع الزمن. فإذا تقاربت المساقط المتوازية لحزمة صغر حجم فضاء الطور، ويسمى النظام في تلك الحالة بأنه نظام انتشاري Dissipative System. وخاصية نظام انتشاري هي انه ينشر طاقة حوله، فيعتبر نظاما مفتوحا. وإذا كان حجم فضاء الطور ثابتا يسمى النظام «نظاما متحفضا». تتصف تلك الأنظمة بكونها أنظمة مغلقة، أي تحوي كل طاقتها. ويصف قانون ليوفيل تلك الحالات رياضيا.
تحليل فضاء الطور[عدل]

تعطينا «صورة فضاء الطور» phase portrait إمكانية تحليل تغير حالة نظام حركي مع الزمن بطريقة بيانية. ونحتاج لذلك معادلات حركة النظام، فلا نحتاج لتمثيل دقيق لتغيره مع الزمن عن طريق، مثلا حل معادلة تفاضلية بطريقة التحليل. ونحصل على بعض النقاط من تحليل فضاء الطور لنظام ثنائي الأبعاد , حيث تصف المعادلتان التفاضليتان ( و ( النظام:
ترسم النقاط بحيث يمثل اتجاه حركة الجسيم في فضاء الطور بمتجه. فإذا اتبعنا اتجاه المتجهات من نقطة معينة فإننا نصل إلى نقطة جديدة نعيد منها تلك العملية. بذلك يمكننا عن طريق مجال المتجهات إضافة مساقط في صورة فضاء الطور، تصف سلوك التغير وصفا تقديريا. فعلى سبيل المثال في حالة رنان فان دير بول نجد أن المساقط تنصب في حلقة دائرية، وهذا ما توضحه المساقط داخل وخارج حلقة الرنين. بالنسبة لأنظمة بسيطة يمكن رسم المساقط ومجال المتجهات باليد، ولكن بالنسبة لأنظمة معقدة فيستحسن إجراء ذلك بالحاسوب.
مراجع[عدل]
- ^ "معلومات عن فضاء الطور على موقع idref.fr". idref.fr. مؤرشف من الأصل في 2020-08-11.
- ^ "معلومات عن فضاء الطور على موقع psh.techlib.cz". psh.techlib.cz. مؤرشف من الأصل في 2020-10-24.
- ^ "معلومات عن فضاء الطور على موقع catalogue.bnf.fr". catalogue.bnf.fr. مؤرشف من الأصل في 2019-05-01.
انظر أيضا[عدل]
- دورة كارنو
- كفاءة تحويل الطاقة
- بقاء الطاقة
- ديناميكا حرارية
- القانون الثاني للترموديناميك
- دورة رانكن
- كفاءة حرارية
- دورة حركة حرارية
| فضاء الطور في المشاريع الشقيقة: | |
| |



