خوارزمية أصل التدرج

أصل التدرج هو خوارزمية تحسين تكرارية من الدرجة الأولى للعثور على الحد الأدنى المحلي لدالة قابلة للاشتقاق. للعثور على الحد الأدنى المحلي للدالة باستخدام منحدر التدرج ، نتخذ خطوات تتناسب مع سلبية التدرج (أو التدرج التقريبي) للدالة عند النقطة الحالية. ولكن إذا اتخذنا بدلاً من ذلك خطوات تتناسب مع إيجابية التدرج ، فإننا نقترب من الحد الأقصى المحلي لهذه الوظيفة ؛ يُعرف الإجراء بعد ذلك بصعود متدرج . تم اقتراح خوارزمية أصل التدرج من قبل العالم الرياضي كوشي في عام 1847.

وصف

رسم توضيحي لأصل التدرج على سلسلة من مجموعات المستويات

يعتمد أصل التدرج على الملاحظة أنه إذا كانت الدالة متعددة المتغيرات $F(\mathbf {x} )$ معرفة و قابلة للاشتقاق في جوار النقطة $\mathbf {a}$ ، فإن$F(\mathbf {x} )$ ينخفض بسرعة أكبرإذا ذهبنا من $\mathbf {a}$ في اتجاه التدرج السلبي لـ $F$ في $\mathbf {a} ,-\nabla F(\mathbf {a} )$ .

ويتبع ذلك أنه إذا كان

$\mathbf {a} _{n+1}=\mathbf {a} _{n}-\gamma \nabla F(\mathbf {a} _{n})$

فإنه لكل $\gamma \in \mathbb {R} _{+}$ صغيرة بما يكفي ، $F(\mathbf {a_{n}} )\geq F(\mathbf {a_{n+1}} )$ . وبعبارة أخرى ، الحد$\gamma \nabla F(\mathbf {a} )$ يطرح من $\mathbf {a}$ لأننا نريد التحرك ضد التدرج نحو الحد الأدنى المحلي. مع أخذ هذه الملاحظة في الاعتبار ، يبدأ المرء بتخمين $\mathbf {x} _{0}$ كحد أدنى محلي $F$ ،و يعتبر بعد ذلك التسلسل $\mathbf {x} _{0},\mathbf {x} _{1},\mathbf {x} _{2},\ldots$ , بحيث:

$\mathbf {x} _{n+1}=\mathbf {x} _{n}-\gamma _{n}\nabla F(\mathbf {x} _{n}),\ n\geq 0.$

لدينا تسلسل رتيب

$F(\mathbf {x} _{0})\geq F(\mathbf {x} _{1})\geq F(\mathbf {x} _{2})\geq \cdots ,$

لذا نأمل أن يكون التسلسل $(\mathbf {x} _{n})$ يتقارب نحو الحد الأدنى المحلي المطلوب. لاحظ أن قيمة حجم الخطوة $\gamma$ يسمح بالتغيير في كل تكرار. مع بعض الافتراضات على الدالة $F$ (فمثلا، $F$ محدبة و $\nabla F$ ليبشيتزية ) وخيارات معينة من $\gamma$ (على سبيل المثال ، يتم اختياره إما عن طريق البحث الخطي الذي يلبي شروط Wolfe ، أو طريقة Barzilai – Borwein الموضحة على النحو التالي) ،

$\gamma _{n}={\frac {\left|\left(\mathbf {x} _{n}-\mathbf {x} _{n-1}\right)^{T}\left[\nabla F(\mathbf {x} _{n})-\nabla F(\mathbf {x} _{n-1})\right]\right|}{\left\|\nabla F(\mathbf {x} _{n})-\nabla F(\mathbf {x} _{n-1})\right\|^{2}}}$

يمكن ضمان التقارب إلى الحد الأدنى المحلي.

عندما تكون الدالة $F$ محدبة ، كل الحدود الدنيا المحلية هي أيضًا حد أدنى عام، لذلك في هذه الحالة يمكن أن يتقارب أصل التدرج إلى الحل العام.

هذه العملية موضحة في الصورة المجاورة. هنا $F$ من المفترض أن يتم تعريفها على المستوى ، وأن الرسم البياني له شكل وعاء . المنحنيات الزرقاء هي الخطوط الكنتورية ، أي المناطق التي تكون فيها قيمة $F$ ثابتة. يظهر سهم أحمر ينشأ عند نقطة اتجاه التدرج السلبي في تلك النقطة. لاحظ أن التدرج (السلبي) عند نقطة ما هو متعامد مع خط الكفاف الذي يمر عبر تلك النقطة. نرى أن أصل التدرج يقودنا إلى قاع الوعاء ، أي إلى النقطة التي تكون فيها قيمة الدالة $F$ هي الحد الأدنى.

أمثلة

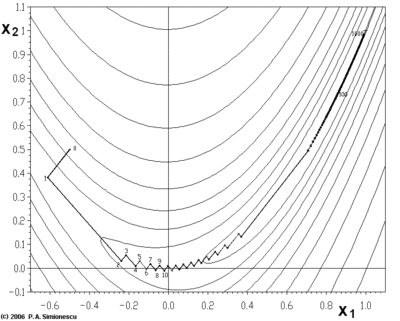
يعاني أصل التدرج من مشاكل في الدوال "المرضية" مثل دالة Rosenbrock الموضحة هنا.

$f(x_{1},x_{2})=(1-x_{1})^{2}+100(x_{2}-{x_{1}}^{2})^{2}.$

تحتوي دالة Rosenbrock على واد منحني ضيق يحتوي على الحد الأدنى. الجزء السفلي من الوادي مسطح للغاية. بسبب الوادي المسطح المنحني يكون التحسين متعرجًا ببطء مع أحجام خطوات صغيرة نحو الحد الأدنى.

يمكننا رؤية مثال آخر على الطبيعة المتعرجة لهذه الطرقية: فلنطبق خوارزمية أصل التدرج على الدالة التالية:

$F(x,y)=\sin \left({\frac {1}{2}}x^{2}-{\frac {1}{4}}y^{2}+3\right)\cos \left(2x+1-e^{y}\right).$

تعليقات

يعمل أصل التدرج في فضاءَات متعددة الأبعاد، حتى في الأبعاد اللانهائية. في الحالة الأخيرة ، تكون مساحة البحث عادةً عبارة عن فضاء دالي ، و نحسب مشتقة Fréchet الخاصة بالدالة التي سيتم تصغيرها لتحديد اتجاه الهبوط.

يمكن أن يستغرق أصل التدرج العديد من التكرارات لحساب الحد الأدنى المحلي بالدقة المطلوبة ، إذا كان الانحناء في اتجاهات مختلفة مختلفًا تمامًا للدالة المحددة. لمثل هذه الدوال، فإن التهيئة المسبقة ، التي تغير هندسة المساحة لتشكيل مجموعات مستوى الوظيفة مثل الدوائر المتحدة المركز ، تعالج التقارب البطيء. ومع ذلك ، يمكن أن يكون إنشاء وتطبيق الشروط المسبقة مكلفًا من الناحية الحسابية.

يمكن دمج أصل التدرج مع بحث خطي ، للعثور على حجم الخطوة الأمثل محليًا $\gamma$ في كل تكرار. يمكن أن يستغرق إجراء البحث الخطي وقتًا طويلاً.

على العكس من ذلك ، باستخدام ثابتة صغيرة $\gamma$ يمكن أن يسفرعن تقارب ضعيف.

يمكن أن تكون الطرق المستندة إلى طريقة نيوتن وانقلاب الهسيان باستخدام تقنيات التدرج المترافق بدائل أفضل. بشكل عام ، تتقارب هذه الأساليب في عدد أقل من التكرارات ، ولكن تكلفة كل تكرار أعلى. ومن الأمثلة على ذلك طريقة BFGS التي تتكون من حساب مصفوفة في كل خطوة يتم من خلالها ضرب متجهة التدرج للذهاب إلى اتجاه "أفضل" ، مقترنًا بخوارزمية بحث خطي أكثر تعقيدًا ، للعثور على القيمة "الأفضل" لـ $\gamma .$

بالنسبة للمسائل الكبيرة للغاية ، حيث تهيمن مشاكل ذاكرة الكمبيوتر ، يجب استخدام طريقة محدودة الذاكرة مثل L-BFGS بدلاً من BFGS أو أصل التدرج.

يمكن النظر إلى أصل التدرج على أنه تطبيق طريقة أويلر لحل المعادلات التفاضلية العادية $x'(t)=-\nabla f(x(t))$ لتدفق متدرج .

أمثلة حسابية

تطبق أمثلة التعليمات البرمجية التالية خوارزمية أصل التدرج للعثور على الحد الأدنى للدالة $f(x)=x^{4}-3x^{3}+2,$ مع مشتقة:$f'(x)=4x^{3}-9x^{2}.$

حل ل $4x^{3}-9x^{2}=0$ وتقييم المشتق الثاني عند الحلول يبين أن الوظيفة لها نقطة هضبة عند 0 والحد الأدنى العام عند $x={\tfrac {9}{4}}.$

بيثون

فيما يلي تطبيق بلغة برمجة Python :

next_x = 6 # We start the search at x=6
gamma = 0.01 # Step size multiplier
precision = 0.00001 # Desired precision of result
max_iters = 10000 # Maximum number of iterations

# Derivative function
def df(x): 
  return 4 * x ** 3 - 9 * x ** 2


for _ in range(max_iters):
  current_x = next_x
  next_x = current_x - gamma * df(current_x)

  step = next_x - current_x
  if abs(step) <= precision:
    break

print("Minimum at ", next_x)

# The output for the above will be something like
# "Minimum at 2.2499646074278457"

سكالا

هنا تنفيذ في لغة برمجة سكالا

import math._
 
val curX = 6
val gamma = 0.01 
val precision = 0.00001 
val previousStepSize = 1 / precision

def df(x: Double): Double = 4 * pow(x, 3) - 9 * pow(x, 2)

def gradientDescent(precision: Double, previousStepSize: Double, curX: Double): Double = {
 if (previousStepSize > precision) {
  val newX = curX + -gamma * df(curX)	
  println(curX)
  gradientDescent(precision, abs(newX - curX), newX)
 } else curX	 
}

val ans = gradientDescent(precision, previousStepSize, curX)
println(s"The local minimum occurs at $ans")

جافا

import java.util.function.Function;
import static java.lang.Math.pow; 
import static java.lang.Math.abs

double gamma = 0.01;
double precision = 0.00001;

Function<Double,Double> df = x -> 4 * pow(x, 3) - 9 * pow(x, 2);
	
double gradientDescent(Function<Double,Double> f) {

	double curX = 6.0;
	double previousStepSize = 1.0;

	while (previousStepSize > precision) {
	  double prevX = curX;
	  curX -= gamma * f.apply(prevX);
	  previousStepSize = abs(curX - prevX);
	}
	return curX;
}
	
double res = gradientDescent(df);
System.out.println(String.format("The local minimum occurs at %f", res));

لغة البرمجة C

ها هي نفس الخوارزمية المطبقة في لغة البرمجة C.

#include <stdio.h>
#include <stdlib.h> 

double dfx(double x) {
  return 4*(x*x*x) - 9*(x*x);
}

double abs_val(double x) {
  return x > 0 ? x : -x;
}

double gradient_descent(double dx, double error, double gamma, unsigned int max_iters) {
  double c_error = error + 1;
  unsigned int iters = 0;
  double p_error;
  while (error < c_error && iters < max_iters) {
    p_error = dx;
    dx -= dfx(p_error) * gamma;
	  c_error = abs_val(p_error-dx);
    printf("\nc_error %f\n", c_error);
    iters++;
  }
  return dx;
}

int main() {
  double dx = 6;
  double error = 1e-6;
  double gamma = 0.01;
  unsigned int max_iters = 10000;
  printf("The local minimum is: %f\n", gradient_descent(dx, error, gamma, max_iters));
  return 0;
}

// adjust training set size

const M = 10;

// generate random training set

const DATA = [];

const getRandomIntFromInterval = (min, max) =>
 Math.floor(Math.random() * (max - min + 1) + min);

const createRandomPortlandHouse = () => ({
 squareMeter: getRandomIntFromInterval(0, 100),
 price: getRandomIntFromInterval(0, 100),
});

for (let i = 0; i < M; i++) {
 DATA.push(createRandomPortlandHouse());
}

const _x = DATA.map(date => date.squareMeter);
const _y = DATA.map(date => date.price);

// linear regression and gradient descent

const LEARNING_RATE = 0.0003;

let thetaOne = 0;
let thetaZero = 0;

const hypothesis = x => thetaZero + thetaOne * x;

const learn = (x, y, alpha) => {
 let thetaZeroSum = 0;
 let thetaOneSum = 0;

 for (let i = 0; i < M; i++) {
  thetaZeroSum += hypothesis(x[i]) - y[i];
  thetaOneSum += (hypothesis(x[i]) - y[i]) * x[i];
 }

 thetaZero = thetaZero - (alpha / M) * thetaZeroSum;
 thetaOne = thetaOne - (alpha / M) * thetaOneSum;
}

const MAX_ITER = 1500;
for (let i = 0; i < MAX_ITER; i++) {
 learn(_x, _y, LEARNING_RATE);
 console.log('thetaZero ', thetaZero, 'thetaOne', thetaOne);
}