تكافؤ (فيزياء)
التكافؤ في الفيزياء (بالإنجليزية:Parity ) هو تماثل بين الحدث وانعكاسه على المرآة.[1][2][3] وفكرة التكافؤ هي أداة مفيدة في حساب ميكانيكا الكم. ويقول علماء الفيزياء إن التكافؤ يكون باقيًا أو محفوظًا على ما هو عليه إذا كان الحدث وصورته في المرآة يتوافقان مع قوانين الطبيعة. وفي هذه الحالة، لا يستطيع المشاهد إدراك الفرق بين الأصل والصورة . ويمكن مشاهدة تلك الخاصية للسلوك الطبيعية في لعبة البلياردو عندما توجد مرآة في الصالة بجوار منضدة البلياردو : نجد أنه لا يوجد فرق في حركة الكرات وتصادمها على منضة البلياردو وبين حركتها في الصورة، هذا هو التكافوء في الفيزياء حيث تنطبق قوانين الحركة سواء في الأصل أو الصورة .
تنطبق نفس القوانين الطبيعية على الأصل والصورة، ولذا فهي لا تضع في يد المشاهد مفتاحًا للتفرقة بينهما. ويكون التكافؤ باقيًا في كل العمليات الحركية و الكهرومغناطيسية الكلاسيكية .
التكافؤ والطبيعة[عدل]
اعتقد علماء الطبيعة فيما مضى أن انحفاظ التكافؤ طبيعي، وينطبق على كل الأحداث. ولكن اثنين من العلماء الصينيين، هما تسونج داو لي، وشين نينج يانج أجريا عددًا من التجارب أثبتت خلاف ذلك. فقد دلت تجاربهما على أن التكافؤ لا يكون باقيًا في الحدث النووي الذي يسمى القوة النووية الضعيفة، ومثال ذلك عملية انبعاث إلكترون من نواة مشعة.
وقد أجريت إحدى التجارب لذلك في المعهد الوطني للمقاييس بالولايات المتحدة، بوساطة سي. أس. وو. من جامعة كولومبيا، بمدينة نيويورك، وكل من أي. أمبلر، وآر. دبليو. هيوارد، ودي. دي. هوبز، وآر. بي. هدسون من المعهد، والذين استخدموا ذرات الكوبالت -60 المشعة. وقد دلت تجاربهم على أن بقاء التكافؤ ليس قانونًا طبيعيًا عامًا.
علاقات متكافئة بسيطة[عدل]
في الفيزياء الكلاسيكية في ظل التناوبات الكلاسيكية المصنفة يمكن أن تكون مجموعات هندسية مثل السكالارس، أو الناقلات.
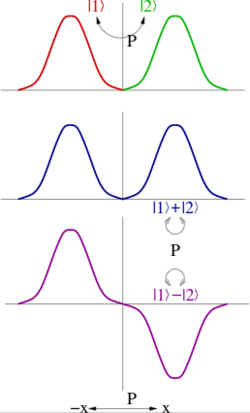
ويمكن للمرء تحديد الانعكاسات مثل الرسم البياني التالي:
المراجع[عدل]
- ^ Wu، C. S.؛ Ambler، E؛ Hayward، R. W.؛ Hoppes، D. D.؛ Hudson، R. P. (1957). "Experimental Test of Parity Conservation in Beta Decay". فيزيكال ريفيو. ج. 105 ع. 4: 1413–1415. Bibcode:1957PhRv..105.1413W. DOI:10.1103/PhysRev.105.1413.
- ^ Bransden، B. H.؛ Joachain، C. J. (2003). Physics of Atoms and Molecules (ط. 2nd). برنتيس هول . ص. 204. ISBN:978-0-582-35692-4.
{{استشهاد بكتاب}}: صيانة الاستشهاد: علامات ترقيم زائدة (link) - ^ Roy، A. (2005). "Discovery of parity violation". Resonance. ج. 10 ع. 12: 164–175. DOI:10.1007/BF02835140.
- Sozzi, M.S. (2008). Discrete symmetries and CP violation. Oxford University Press. ISBN:978-0-19-929666-8.
- CP violation, by I.I. Bigi and A.I. Sanda (ISBN 0-521-44349-0)
- Weinberg, S. (1995). The Quantum Theory of Fields. Cambridge University Press. ISBN:0-521-67053-5.
- Roy, A. "Discovery of parity violation." Resonance 10 (12):164-175 (2005) (ISSN 0971-8044)


