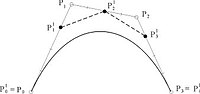
في التحليل العددي، خوارزمية دوكاستلجو (نسبة إلى مبتكره بول دوكاستلجو)، هو طريقة تكرارية لتقييم كثيرات حدود في صورة بيرنستين أو منحنيات بيزير. يمكن استعمالها أيضاً في فصل منحنى بيزير مفرد إلى منحنيات بيزيرية عند قيمة وسيطة اختيارية.
بالرغم من بطء هذا الخوارزم مقارنة بالطريقة المباشرة إلّا أنه أكثر استقراراً عددياً.
تعريف[عدل]
لتكن كثيرة الحدود B في صورة بيرنستين من الدرجة n

حيث b هي متعددة الحدود لبيرنشتاين أساسية، تكون كثيرة الحدود عن نقطة t0 قابلة للتقييم بفضل علاقة التكرار.


حينئذ، يكون تقييم  عند نقطة
عند نقطة  ممكناً في
ممكناً في  خطوة من الخوارزم. وتعطى النتيجة
خطوة من الخوارزم. وتعطى النتيجة  بالعلاقة:
بالعلاقة:

بالإضافة لذلك، يمكن فصل منحنى بيزيه  عن نقطة
عن نقطة  إلى منحنيين بنقطتي تحكم متتاليتين:
إلى منحنيين بنقطتي تحكم متتاليتين:


مثال للتضمين[عدل]
المثال التالي يتضمن خوارزم كاستلجو بلغة هاسكل:
import Data.Array
deCasteljau::Array Int (Double,Double)->Double->(Double,Double)
deCasteljau controls t0=
coefs!(0,n)
where
(c0,n)=bounds controls
coefs=listArray ((0,0),(n,n)) $ map deCasteljau' [(i,j) | i<-[0..n], j<-[0..n]]
deCasteljau' (i,0)
| i>=c0 = controls!i
| otherwise = 0
deCasteljau' (i,j) =
let (x0,y0)=coefs!(i,j-1)
(x1,y1)=coefs!(i+1, j-1)
in ((1-t0)*x0 + t0*x1, (1-t0)*y0 + t0*y1)
ملاحظات[عدل]
عند تنفيذ الحسابات يدوياً سيكون من الأجدر تدوين المعاملات في مخطط مثلثي كما يلي

عن وقع الاختيار عند نقطة t0 لتقييم كثيرة حدود بيرنستين، بإمكاننا استعمال قطري المخطط المثلثي لإنشاء قسمة كثيرة الحدود.
![{\displaystyle B(t)=\sum _{i=0}^{n}\beta _{i}^{(0)}b_{i,n}(t){\mbox{ , }}\qquad t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb84d69bb346f499c657d7e0737dda3ee72535fa)
إلى
![{\displaystyle B_{1}(t)=\sum _{i=0}^{n}\beta _{0}^{(i)}b_{i,n}\left({\frac {t}{t_{0}}}\right){\mbox{ , }}\qquad t\in [0,t_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddb872182151fb849a91f142f00b0a7ecb6c0eed)
و
![{\displaystyle B_{2}(t)=\sum _{i=0}^{n}\beta _{n-i}^{(i)}b_{i,n}\left({\frac {t-t_{0}}{1-t_{0}}}\right){\mbox{ , }}\qquad t\in [t_{0},1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/872c66d5d31371d8f6b61cf3b585865a6f489024)
نرغب بتقييم كثيرة حدود بيرنستين من الدرجة 2 بمعاملات بيرنستين



عند النقطة t0.
نستهل المعاودة بـ


وبالتكرار الثاني يتوقف الاستدعاء الذاتي مع

وهي كثيرة الحدود المتوقعة من الدرجة n.
انظر أيضا[عدل]













![{\displaystyle B(t)=\sum _{i=0}^{n}\beta _{i}^{(0)}b_{i,n}(t){\mbox{ , }}\qquad t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb84d69bb346f499c657d7e0737dda3ee72535fa)
![{\displaystyle B_{1}(t)=\sum _{i=0}^{n}\beta _{0}^{(i)}b_{i,n}\left({\frac {t}{t_{0}}}\right){\mbox{ , }}\qquad t\in [0,t_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddb872182151fb849a91f142f00b0a7ecb6c0eed)
![{\displaystyle B_{2}(t)=\sum _{i=0}^{n}\beta _{n-i}^{(i)}b_{i,n}\left({\frac {t-t_{0}}{1-t_{0}}}\right){\mbox{ , }}\qquad t\in [t_{0},1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/872c66d5d31371d8f6b61cf3b585865a6f489024)





