مبدأ التراكب

تراكب موجات مستوية (عرضية) وموجات ناشئة عن حركة البط في الماء .

مبدأ التراكب في الفيزياء (بالإنجليزية: superposition principle) ينص على أنه في جميع الأنظمة الخطية تكون محصلة تأثيرين أو أكثر عبارة عن مجموع التأثيرين . فإذا كان التأثير A يحدث الناتج X والتأثير B ينتج الناتج Y فإن التأثيرين (A + B) ينتجان (X + Y).

التراكب هو أحد الشروط الضرورية لاعتبار دالة "دالة خطية". ومن خواص الدالة الخطية أنها تفي بخاصية التراكب بالجمع ، وأن تكون أيضا متجانسة من الدرجة الأولى (يجري عليها الضرب المعتاد scalar multiplication وتعرف بالمعادلة:

$F(x_1+x_2+\cdots)=F(x_1)+F(x_2)+\cdots$ (تراكب)

$F(a x)=a F(x)$

يطبق مبدأ التراكب في الموجات الكهرومغناطيسية وفي البصريات وفي تقنية الاتصلات وفي جمع القوى في الميكانيكا الكلاسيكية وفي الحالات الكمومية ميكانيكا الكم.

رياضيا

يمكن تمثيل التراكب بدالة خطية :

$x(t) = \sum_{i=1}^{n}{\alpha_i x_i(t)}$

حيث يعني الجمع أن دالات أو كميات $x_i(t)$ من نفس النوع يمكن جمعها لتكوين كمية جديدة $x(t)$. ويعطي المعامل $\alpha_i$ نسبة (تأثير) كل من الكميات المكونة لها .

تنطبق مبدأ التراكب على كثير من الأنظمة ، وعلى المعادلات التفاضلية الخطية. فإذا كان لمعادلة تفاضلية خطية حلين $f_1$ و$f_2$, فيشكل مجموعهما أيضا حلا $f_1 + f_2$ للمعادلة .

وبصفة عامة :

"إذا كانت $f_1$ حتى $f_n$ حلولا لمعادلة تفاضلية خطية ، فيكون كل مجموع لهذه الحلول أيضا حلا للمعادلة التفاضلية ."

تداخل الموجات

مقال تفصيلي :تداخل

combined waveform
wave 1
wave 2
	موجتان في نفس الطور	موجتان بفرق طور 180°

يعني التراكب في علم الموجات تداخل موجات لها نفس طول الموجة . ويهما في هذه الحالة قيمة مطال كل الموجة . فيمكن على سبيل المثال تداخل عدة أمواج مائية أو عدة أمواج كهرومغناطيسية فإما أن تقوى بعضها أو تضعف محصلتها .

تداخل موجتين.

تتصف الدالة الموجية الناتجة $\Psi(\vec x, t)$ بالخاصية:

$\Psi(\vec x, t) = \sum_{i=1}^n \Psi_i(\vec x, t)$

حيث :

$\Psi_i(\vec x, t)$ الدوال الموجية للموجات الأصلية.

في الميكانيكا الكلاسيكية

متوازي أضلاع القوى: السهم الأحمر هو محصلة القوتين F1 و F2.

مقال تفصيلي :متوازي أضلاع القوى

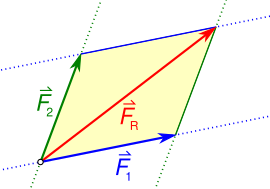
تتراكب أيضا القوى الميكانيكية. وتسمى هذه الخاصية أحيانا "القانون الرابع لنيوتن".

صيغتها الرياضية كالآتي:

$\vec F = \sum_{i=1}^{n} \vec F_i$

هذه المعادلة تقول أن القوى المختلفة العاملة على أحد الأجسام يمكن اختصرها في "محصلة" تقوم مقامهم .

مثال على ذلك نجده في صندوق نقوم بإزاحته عن موضعه : لا يوجد فرق بين أن نزيح الصندوق إلى الأمام أولا ثم إلى اليمين أو أن نزيحه في خط مباشر عرضي في الاتجاه الأمامي-اليميني .

في ميكانيكا الكم

مقال تفصيلي :تراكب كمي

يماثل التراكب في ميكانيكا الكم التراكب في الميكانيكا الكلاسيكية حيث أن الحالات الكمومية توصف أيضا بدوال موجية. مع ملاحظة أن الدوال الكمومية الموجية ليست "حقيقية" كما هو في الحالة الكلاسيكية . في ميكانيكا الكم يعبر عن تراكب متجهات الحالة بجمع متجهات .

يعبر عن ذلك رياضيا بالصيغة "برا-كيت" Bra-Ket :

$|\psi\rangle=\sum\limits_{i=1}^n c_i|\varphi_i\rangle$

تلك المعادلة تقول أن الحالة الكلية $|\psi\rangle$ تتكون من تراكب عدة حالات $|\varphi_i\rangle$ وتصفها تماما. وهي لذلك تسمى "تراكب الحالة" . فإذا كانت تلك الحالات $|\varphi_i\rangle$ موحدة فيما بينها فتعطي مربعات القيم $|c_i|^2$ "المطالات المحتملة " $c_i$ ، أي تعطي أحتمال الحصول على نتيجة القياس في الحالة التي تخصها .

في الكهرباء

ينطبق مبدأ التراكب على التيار الكهربائي وعلى الجهد . كما ينطبق على حسابات التيار المتردد المركبة لحساب التيار المتردد والجهد المتردد . وينطبق المبدأ بصفة عامة على الدوائر الكهربائية فقط المكونة من وحدات تعمل خطيا.

اقرأ أيضا

• متوازي أضلاع القوى
• تراكب كمي
• مضلع القوى
• متجه