نبضة (صوت)
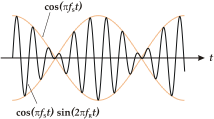
في علم الصوت، الخفقة هي تداخل موجات بين صوتين ذواتي ترددين مختلفين اختلافاً طفيفاً. ينظر إليها على أنها اختلافات دورية في المقدار ومعدل هذه الاختلافات يكون بطرح قيمة الترددين. بالنسبة لآلات الضبط الموسيقية التي يمكن أن تنتج نغمات مستدامة، يمكن التعرف بسهولة على النبضات. إن ضبط نغمتين منسجمتين سيكون له تأثير غريب: عندما تكون النغمتان متقاربتان لكن غير متطابقتان، تنتج النبضات عن الفرق في التردد. يختلف المقدار كما في التريمولو إذ أن الأصوات تتداخل بالتناوب. عندما تتقارب النغمتان تدريجياً في انسجام، يتباطئ التنابض وقد يصبح غير ملموس.
رياضيات وفيزياء[عدل]
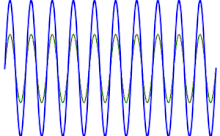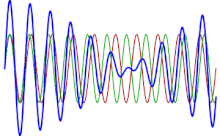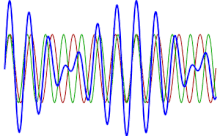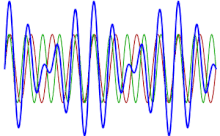
تتجلى هذه الظاهرة سمعياً. إذا رسمنا مخططاً يظهر دالة المجموع الصوتي لوترين، فإنه يمكن معرفة أن القيم العظمى والقيم الصغرى لم تعد ثابتة كما هو الحال عندما تكون النغمة نقية، لكنها تتغير مع الوقت: عندما يكون طور الموجتين حوالي 180 درجة، تلغي القيمة العظمى لإحدى الموجتين القيمة الصغرى للموجة الأخرى، في حين عندما تكونان في نفس الطور تجمع قيمهما العظمى، ما يرفع المقدار.
يمكن برهنة أن القيم المتتعابقة للقيم القصوى والصغرى تشكّل موجة يساوي ترددها الفرق بين ترددات الموجتين البدائيتين. (طالع قائمة المطابقات المثلثية) يمكن توضيح أبسط الحالات، بين منحنى الجيب لهما:
مراجع[عدل]
- ^ "Interference beats and Tartini tones", Physclips, UNSW.edu.au. نسخة محفوظة 05 أغسطس 2017 على موقع واي باك مشين.
| في كومنز صور وملفات عن: نبضة |


