جسيم مضاد
| صنف فرعي من | |
|---|---|
| يدرسه | |
| التفاعل | |
| محدد موقع الموارد المُوحَّد |
| ||
| الإفناء | ||
الأدوات | ||
الإستخدامات | ||
الهيئات | ||
الأشخاص | ||
معظم أنواع الجسيمات، يوجد لها هناك جسيم مضاد (بالإنجليزية: Antiparticle) مساو لها في الكتلة الساكنة والدوران المغزلي والعمر وتماما في قيمة الشحنة الكهربائية لكن معاكس لها فيها.[1][2][3] فعلى سبيل المثال، الجسيم المضاد لإلكترون يكون موجب الشحنة ويسمى بوزيترونا، وينتج بشكل طبيعي في حالات خاصة من الاضمحلال الإشعاعي.
قوانين الطبيعة تكون متماثلة بشكل قوي فيما يتعلق بالجسيمات والجسيمات المضادة. فمثلا، عندما يتحد نقيض بروتون مع بوزيترون فإنهما يشكلان ذرة من نقيض الهيدروجين، والتي تكون مشابهة تماما من حيث خواصها لذرة الهيدروجين. فالفيزيائي الذي يكون جسمه مصنوعا من مادة مضادة، وينجز تجربة في مختبرعلمي مصنوع أيضا من مادة مضادة، ويستخدم مواد كيميائية ومواد متكونة من جسيمات مضادة، فستظهر له تقريبا نفس النتائج في جميع التجارب. وهذا يقود إلى السؤال وهو أنه بعد الانفجار الكبير لماذا تكون الكون كله من المادة بدلا من أن يكون نصفه من المادة والنصف الآخر من مادة مضادة. عندما يلتقي جسيم مع مضاده، تحدث ظواهر شديدة العنف إذ تتحرر كمية كبيرة من الطاقة إثر هذا اللقاء، فيتفانى الجسيم ومضاده تماماً ويتحولان بالكامل إلى طاقة مما ينتج الفوتون، بما أن شحنتا الجسيم والجسيم المضاد متعاكستان، فإن الشحنة تحفظ. فمثلا، تتحلل الإلكترونات المضادة الناتجة بدورها عن تحلل إشعاعي طبيعي بسرعة مع الإلكترونات مشكلة زوجا من أشعة غاما.
الجسيمات المضادة تنتج بشكل طبيعي من تحلل بيتا، وأيضا من تفاعل للأشعة الكونية في الغلاف الجوي. وبما أن الشحنة تكون ثابتة، فإنه من غير الممكن إنتاج جسيمات مضادة إلا إذا تم تدمير الجسيم من نفس الشحنة (كما في تحلل بيتا)، أو إنتاج جسيم من شحنة مضادة. وقد تم عمل الفكرة الثانية في العديد من العمليات حيث تم إنتاج الجسيم وضديده بوقت واحد، كما هو في معجل الجسيمات. وتعتبر تلك عملية إفناء عكسية للجسيم-ومضاد الجسيم.
بما أن الجسيم وضديده لهما شحنتان متعاكستان فإن الحيود الكهربائي للجسيم لا يستلزم أن يكون الجسيم متطابقا مع ضديده. فمثلا، النيوترون مكون من الكواركات ومضاد النيوترون مكون من مضادات الكواركات، ويمكن التمييز بينهما لأنهما سيقضيان عند الاتصال. وهناك بعض الجسيمات (أو الدقائق بمسمى آخر) التي ليس لها شحنة كهربائية ولا باريونية ولاغيرها على الإطلاق، كالفوتون والجرافتون وهو جسيم افتراضي والجسيم الثقيل الافتراضي الضعيف التفاعل (WIMP) وهذان يسميان (ماجورانا), لا يوجد فرق بينها ومضاداتها، فيصح القول إن الفوتون المضاد مطابق للفوتون، أو بتعبير آخر فإنه في حالة الفوتون لا يمكن تمييز الجسيمات عن مضاداتها، أو الجسيمات نفسها متناظرة، لا شيء آخر مناظر لها.
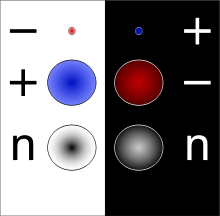
البداية[عدل]
التجربة[عدل]
في عام 1932 وبعد أن تنبأ بول ديراك بوجود البوزيترون، اكتشف كارل أندرسون بأن اصطدامات الأشعة الكونية تنتج تلك الجسيمات داخل غرفة خاصة. فقد أظهر كاشف الجسيمات (بالإنجليزية: Particle detector) أو كاشف الإشعاع (بالإنجليزية: radiation detector) عن أثر ينحني في الاتجاه المعاكس لمسار الالكترونات ضمن الحقل المغناطيسي، ثم أمكن قياس كتلة الجسيم المضاد، وسمي (بوزيترون).
تم اكتشاف مضاد البروتون ومضاد النيوترون عن طريق اميليو سجري وأوين تشامبرلين عام 1955 بجامعة كاليفورنيا. وبعدها تم إنتاج مضاد الجسيمات للعديد من الجسيمات تحت الذرية عن طريق تجارب مسرع الجسيمات.
نظرية الثقب[عدل]
تضمنت نتائج حل معادلة ديراك على وجود كمية من الطاقة السالبة، كنتيجة أن الإلكترون يمكنه إطلاق أشعة بشكل مستمر مما يوقعه في حالة من الطاقة السلبية. ويمكن احتمال الأسوأ وهو أن يستمر بإطلاق كمية لا متناهية من الطاقة بسبب توافر كمية غير منتهية من حالات الطاقة السلبية. ولمنع هذا الوضع غير طبيعي من الحدوث، فقد اقترح ديراك بأن هناك بحرا من الإلكترونات ذات طاقة سلبية تملأ هذا المحيط، تغطي جميع حالات الطاقة المنخفضة بحيث خلال مبدأ استبعاد باولي فلا يمكن لأي الكترون آخر أن يقع بهذا البحر. مع ذلك في بعض الأحيان، قد تنتشل إحدى الجسيمات سلبية الطاقة من بحر ديراك لتصبح جسيم موجب الطاقة. لكن عند خروجها فإنها ستترك وراءها ثقب في البحر والتي ستعمل تماما كما الكترون موجب الطاقة ولكن بشحنة معاكسة، وافترض بأنها البروتونات، وقد أطلق على ورقة عمله تلك اسم نظرية الإلكترونات والبروتونات (بالإنجليزية: A theory of electrons and protons).
كان ديراك مدركا بمشكلة أن الصورة التي عملها تتضمن على عدد غير متناه من الشحنات السالبة. وقد احتج بأن ندرك بأنها الحالة العادية للشحنة الصفرية. الصعوبة الأخرى هي الاختلاف بالكتلة ما بين الإلكترون والبروتون. وقد جادل ديراك أيضا بأن ذلك سببه التفاعلات الكهروطيسية مع البحر، حتى أثبت هيرمان ويل بأن هناك تناسق تام ما بين الشحنات الموجبة والسالبة في نظرية الثقب. وقد تنبأ ديراك بالتفاعل
e−
+
p+
→
γ
+
γ
حيث يقضى الإلكترون والبروتون على بعضهما فينتج منهما 2 فوتون. واثبت كلا من روبرت أوبنهايمر وايغور تام بأن ذلك يجعل المادة الطبيعية تختفي بسرعة كبيرة. وبعدها بسنة، أي عام 1931، عدل ديراك من نظريته وافترض البوزيترون، وهو جسيم له نفس كتلة الإلكترون. واكتشف هذا الجسيم في السنة التالية مما أزاح آخر اعتراضين لتلك النظرية.
لكن تبقى مشكلة العدد اللانهائي من الشحنات موجودة بالمحيط. وكما نعلم أيضا أن البوزونات لديها جسيمات مضادة، ولكن بما أنهم لم يخضعوا لنظرية مبدأ استبعاد باولي، فإن نظرية الثقب لا تتوافق معهم. لذا فالتفسير الموحد للجسيمات المضادة اتاحته نظرية المجال الكمي والتي حلت كلا من المشكلتين.
إفناء جسيم-جسيم مضاد[عدل]

إذا كان الجسيم وضديده بحالة كمية مناسبة، فإنهما سيفنيان بعضهما مكونين جسيمات محايدة (كالفوتونات)، التفاعلات مثل
e−
+
e+
→
γ
+
γ
(ينتج من إفناء زوج إلكترون-بوزيترون عدد 2 فوتون).
لذا فلا يمكن الحصول على فوتون مفرد ناتج من الإناء زوج الكترون-بوزيترون
e−
+
e+
→
γ
لأنه من غير الممكن المحافظة على الطاقة وكمية الحركة معا في تلك العملية، ولا يمكن أيضا إجراء عملية معاكسة لذات السبب. ولكن بنظرية المجال الكمي فإن تلك العملية مسموحة كحالة كم مرحلية لزمن قصير يكفي باستيعاب انتهاك حفظ الطاقة عن طريق مبدأ الريبة. بذلك يفتح لنا المجال لإنتاج أو الإناء زوج افتراضي (أو الواقعي) بحيث حالة جسيم كمي قد تتأرجح إلى حالة جسيمين ثم تعود. تلك العمليات ضرورية في حالة الفراغ أو إعادة تنظيم لنظرية المجال الكمي. وأيضا تفتح المجال لخلط الجسيمات المحايدة خلال عمليات مثل التي بالصورة: وهو مثال معقد لما يسمى إعادة تنظيم للكتلة (mass renormalization).
خصائص الجسيمات المضادة[عدل]
يمكن أن تتبادل حالة كمية لكل من الجسيم وضديده وذلك بتفعيل مشغلات تماثل الشحنة C-symmetry C، مشابه الشحنة Parity P، ومعاكس الزمن time reversal T. إذا كانت العلامات |p,σ,n> تدل على حالة الكم للجسيم n مع العزم p، الدوران المغزلي J ويكون عنصره بالإتجاه-z هو σ فإن أحداهما يكون:
حيث:nc يرمز إلى حالة تماثل الشحنة. أي أن الجسيم المضاد الذي يتصرف تحت CPT (مماثل الشحنة ومشابه الشحنة ومعاكس الزمن) يكون بنفس حالة الجسيم ويقع ضديده تحت نفس النموذج المبسط لمجموعة بيونكير (Poincare group). فقد تكون خصائص الجسيمات المضادة متصلة بالجسيم خلالها. إن كان T بحالة تماثل ديناميكي جيد، فالنتيجة هي:
حيث علامة التناسب تشير إلى أنه قد يكون هناك طور على جهة اليمين. وبمعنى آخر فإن الجسيم وضديده يجب أن يكون:
- نفس الكتلة m
- نفس حالة الدوران المغزلي J
- متعاكس بالشحنة الكهربائية q و-q.
نظرية المجال الكمي[عدل]
يعتمد هذا الفصل على أفكار ولغة وترميز قانونية تجزئة الكم (canonical quantization) لنظرية المجال الكمي.
قد يحاول المرء تقسيم مجال الإلكترون بدون أن يخلط عوامل الإفناء مع الإنشاء من خلال كتابة
فعندما يستخدم الرمز k للإشارة إلى أعداد الكم p وσ تم ذكره في المقطع السابق ورمز الطاقة، (E(k, وak ترمز إلى عوامل الإفناء المتشابهة. وبما أننا نتعامل مع الفرميونات، فيجب أن يكون لدينا علاقة مضادة التبادل مرضية قانونيا. ولكن إن كتب قانون هاملتون كالتالي
فإنه سوف يُرى أن القيمة المتوقعة ل H يجب أن لا تكون موجبة. وهذا بسبب أنه بإمكان (E(k أن يكون لها أي علامة أيا كانت، وهذا المزيج من عاملي الإنشاء والإفناء له قيمة متوقعة وهي: 1 أو 0.
لذا يجب إدخال شحنة متماثلة في مجال الجسيم المضاد مع عواملها للإفناء والتكوين لتحقيق تلك الروابط
حيث k مساوية ل p، ومعاكسة في σ وعلامة الطاقة. وعندها سيتم إعادة كتابة المجال بالصيغة التالية:
حيث المجموع الأول سيكون حالة طاقة موجبة والمحصلة الثانية هي حالة طاقة سلبية. وستكون الطاقة كالتالي:
حيث E0 هي ثابت سلبي لانهائي. وتعرف حالة الفراغ بأنها الحالة التي لايوجد بها جسيمات ولا أضدادها، أي و. عندها تكون طاقة الفراغ تساوي بالضبط E0. حيث أن قياس جميع الطاقات مرتبطة بالفراغ، فإن H هو موجب محدد. بتحليل خصائص كل من ak وbk يظهر بأن أحدهما هو عامل الإناء للجسيم والآخر للجسيم المضاد. وتلك هي حالة الفرميون.
هذا المنهج عمله كل من فلاديمير فوك وونديل فوري وروبرت ابنهايمر. إذا تم تجزئة الكم بمجال سلّمي حقيقي، فسيكون هناك نوع واحد لعامل الإفناء، لذا فمجال التدرج الحقيقي يصف البوزون المحايد. حيث أن مجالات التدرج المعقدة تتسع لنوعين مختلفين من عوامل الإفناء، والتي تتصل ببعضها عن طريق الاقتران، وتلك المجالات تصف البوزونات المشحونة.
تفسير فينمان-ستوكلبيرغ[عدل]
مع الأخذ بعين الاعتبار ان صيغ انتشار الطاقة السالبة للمجال الإلكتروني تكون عكسية مع الزمن، فقد توصل ارنست ستوكلبيرغ إلى تصور حي للحقيقة القائلة بأن الجسيمات وأضدادها لها نفس الكتلة m والدوران المغزلي J ولكن متعاكسة بالشحنة q. مما سمح له بإعادة كتابة نظرية الاضطراب بدقة على شكل رسوم بيانية. وقدم بعدها ريتشارد فاينمان استنتاج منهجي مستقل لتلك الرسوم البيانية من شكليات الجسيم وسميت بمخطط فاينمان. كل خط من الخطوط البيانية تمثل انتشار الجسيم سواء طردي أو عكسي مع الزمن. وتلك التقنية هي طريقة واسعة الانتشار في الوقت الحالي لاحتساب السعة في نظرية المجال الكمي.
وبما أن التصور قد طوره ارنست ستوكلبيرغ واكتسب صيغته المحدثة بمجهودات فيمان، لذا فقد سمي بتفسير فينمان-ستوكلبيرغ للجسيمات المضادة تكريما لكلا العالمين.
انظر أيضا[عدل]
المراجع[عدل]
- ^ "معلومات عن جسيم مضاد على موقع dx.doi.org". dx.doi.org. مؤرشف من الأصل في 2019-12-16.
- ^ "معلومات عن جسيم مضاد على موقع thes.bncf.firenze.sbn.it". thes.bncf.firenze.sbn.it. مؤرشف من الأصل في 2019-12-16.
- ^ "معلومات عن جسيم مضاد على موقع esu.com.ua". esu.com.ua. مؤرشف من الأصل في 2019-12-16.
- المادة المضادة الكونية مجلة العلوم أغسطس - سبتمبر1998 / المجلد 14.
- Feynman, Richard P. "The reason for antiparticles", in The 1986 Dirac memorial lectures, R.P. Feynman and S. Weinberg. Cambridge University Press, 1987. ISBN 0-521-34000-4.
- Weinberg, Steven. The quantum theory of fields, Volume 1: Foundations. Cambridge University Press, 1995. ISBN 0-521-55001-7.
| جسيم مضاد في المشاريع الشقيقة: | |
| |












