هزاز توافقي (ميكانيكا الكم)
هزاز توافقي كمومي (بالإنجليزية: quantum harmonic Oscillator) في الفيزياء وميكانيكا الكم، يصف الهزاز التوافقي الكمومي في ميكانيكا الكم -مثلما يصف الهزاز التوافقي في الميكانيكا الكلاسيكية- حركة جسيم في جهد توافقي. ففي ميكانيكا الكم يعامل الجسيم على أنه دالة موجية بعكس الميكانيكا الكلاسيكية التي تتعامل مع الجسيم كجسيم دون تغيير أيا من حالاته.
ومثال من الفيزياء تتعامل الميكانيكا الكلاسيكية مع جسيم نقطي مرتبط بلولب يهتز ومع اعتبار أن تلك النقطة المادية (الجسيم) تهتز في جهد توافقي (اللولب) شكله:
وبناء على ذلك تتأرجح النقطة المادية علي جهتي نقطة السكون بحيث تكون الإزاحة عن نقطة السكون متناسبة مع القوة التي تؤثر عليها لإعادتها إلى نقطة السكون:
حيث ثابت اللولب.
أمثـــلة[عدل]
يشكل الهزاز التوافقي نموذجا مهما للأنظمة في الفيزياء الكمومية وهي تصف خواص حركة الجسيمات الصغيرة مثل إلكترون في جهد النواة الذرية. بواسطتها نستطيع وصف عدة من الخواص الفيزيائية لتلك الأنظمة الصغرية بطريقة مقربة ناجحة، لم تستطع الميكانيكا الكلاسيكية (قوانين نيوتن مثلا) في معالجتها والإتيان بحلول صحيحة تتفق مع الواقع. ومن تلك الأنظمة التي يصفها الهزاز التوافقي الكمومي
- في فيزياء الجزيئات يمكن لنموذج الهزاز التوافقي الكمومي حساب حالة الترابط بين الذرات، ويعطي طيف الإهزازات بدقة متناهية. وتتخذ الميكانيكا الكم الجزيئ كنموذج الهزاز التوافقي في حالة ذرتين مرتبطتن بلولب بينهما (جهد توافقي) وتهتزان ضد بعضهما البعض:

وتؤدي القوة الخطية عمل اللولب المماثل لجهد توافقي (متناسبة مع ) حيث الإزاحة.
ولكن في الجزيئات يختلف الجهد عن هذا الجهد الذي افترضناه للهزاز التوافقي، إلا أن الهزاز التوافقي المفترض هنا يعطي الحل الصحيح للاهتزازات المنخفضة الطاقة.
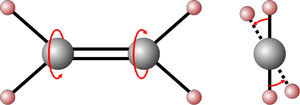
وفيه تعوج الرابطة الثنائية وتهتز ذرتين من ذرات الهيدروجين بطريقة محدرجة (فتلية) ضد بعضهما.
- في الفيزياء الذرية تُحصر الذرات المراد إجراء تجارب عليها فيما يسمى مصيدة مغناطيسية أو مصيدة أيونات وتبرد فيها لإجراء التجارب عليها. كما يمكن دراسة حالات المادة المتجمعة مثلما في مكثف بوز-أينشتاين أو مكثف فيرمي. في تلك الحالات يستخدم جهد زائدي (في هيئة قطع زائد) كمرحلة أولى تقريبية فيمكن معاملتها بطريقة الهزاز التوافقي الكمومي والحصول على حلول تقريبية أولية.
- في فيزياء الجوامد يصف نموذج أينشتاين الذي صاغه ألبرت أينشتاين طريقة لتعيين الجزء الذي تشارك به اهتزازات الشبكة البلورية (فونونات) في السعة الحرارية للبلورات، وتعيينها حسابيا. ويعتبر نموذج أينشتاين أن المادة الصلبة مكونة من عدد من الهزازات التوافقية الكمومية، تهتز في ثلاثة أبعاد للمكان، وأن كل منها يهتز دون تأثير من الآخر. يعطي هذا النموذج المبسط حلولا تقريبية لا بأس بها.
وعلاوة على ذلك فيمكن أن يكون هناك تأثير بين الاهتزازات في الشبكة البلورية حيث تكون الذرة واقعة تحت تأثير جهد معين من جاراتها من الذرات، وهذا ما يحدث فعلا في طبيعة الجوامد.
تأريخ[عدل]
في عام 1900 قام الفيزيائي الألماني ماكس بلانك بصياغة معادلة تصف توزيع الترددات التي يقيسها والصادرة من جسم أسود ساخن، حيث اعتبر ان الجسم الأسود مكون من عدة من الهزازات التوافقية، وكل منها يهتز بطاقة منفصلة (أي باعتبار أن الأشعة الحرارية الصادرة ذات مقادير معينة منفصلة (سلميّة)، وليست ترادداتها مستمرة). .[1]
انظر تاريخ تطور ميكانيكا الكم.
مقدمـــة[عدل]
تعالج معادلة هاميلتون في حالة جسيم له كتلة m يهتز في جهد توافقي . (حركة الإلكترون حول نواة الذرة في مجالها الكهربائي، تمثل نموذجا لتلك الحركة التوافقية.)
حيث , و (أوميجا) هي التردد الذاتي لهزاز توافقي، والمعادلة لطاقة الجسيم الكلية في هذه الحالة هي:
وتصف معادلة هاميلتون الطاقة الكلية للنظام، أي أنها مجموع طاقة الحركة (وهي الجزء الأول) وطاقة الوضع الثقالية (وهي الجزء الثاني).
والأن نستبدل دليل المكان وزخم الحركة بمعاملاتها الكمومية لدخل ضمن نطاق التكميم الميكانيكي، حيث:
وتسمى معامل نابلا [Nabla-Operator]
(ملحوظة " السهم فوق المتغير معناه أننا نتعامل مع متجهات وبالتالي لا بد من اتباع مبادئ حساب المتجهات.)
وفي الشكل الأخير قمنا بصياغة معامل المكان، وبالتالي تتغير صيغة معادلة هاميلتون إلى صيغة معامل هاميلتون الذي يعبر عن التغير في موضع الجسيم حيث يمكننا كتابة المعامل كالتالي:
حيث يسمى معامل لابلاس [ Laplace-Operator].
ويختصر معامل نابلا في حالة الحركة على المحور السيني وحده إلى المشتقة التفاضلية .
سوف نتعامل مع حل تلك المسألة في حالة حركة الجسيم في اتجاه واحد فقط، وفي المحور .
معادلة شرودنجر للنظام[عدل]
عن طريق معامل هاميلتون الموصوف اعلاه نحصل على معادلة القيم الذاتية eigenvalue equation للهزاز التوافقي -(وهي معادلة شرودنجر المستقرة، أي التي لا تتغير مع الزمن).
- ,
وفي الصيغة التي تسمح بتغير مكان الجسيم فقط:
في ميكانيكا الكم نتعامل مع الجسيم ليس كنقطة مادية وأنما نصفه بصفاته الموجية (موجة مادية)، والدالة الموجية للجسيم هنا هو الرمز ، وهو يحمل صفات الجسيم.
خواص حلول معادلة شرودنجر[عدل]
الدوال الذاتية[عدل]

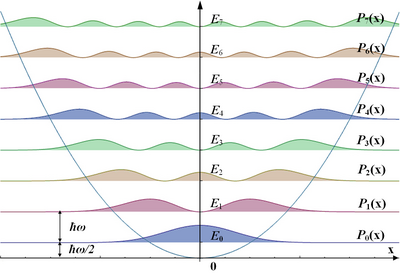
تنتج عن حل معادلة شرودنجر التفاضلية الدوال الذاتية للهزاز التوافقي. وتسمى دوال هيرميت :
- .
حيث كثيرة الحدود لهيرميت.
ويصف الجزء التناقص الأسي لاحتمال وجود الجسيم خارج جهد الهزاز. (في الفيزياء نشبه جهد الهزاز المؤثر على الجسيم بوجود الجسيم في «بئر جهدي»، وبهذا يكون احتمال وجود الجسيم خارج البئر صغير جدا، وهذا ما تعبر عنه الدوال الموجية الموضعية للجسيم في الشكل).
الحالة القاعية وهي حالة أقل طاقة للجسيم هي المنتسبة إلى وهي في شكل منحنى جاوس، ويلاحظ أنها ممثلة بنصف طول موجة.
- .
ويبين الشكل العلوي الثمانية حالات الأولى لحلول معادلة شرودنجر ، وهي تسمى الدوال الذاتية. وإلى جانب الدوال الموجية للجسيم في حالات الطاقة يصف الشكل السفلي مربع قيمة الدالة الموجية، وهو يعطي احتمال وجود الجسيم في الجهد التوافقي المفترض (والجهد التوافقي هنا موصوف بالمنحنى الأزرق).
معنى الدوال الذاتية أنها دوال منفصلة وليست مستمرة، فكل دالة تتحقق بوجود عدد كامل من طول موجة الجسيم ماعدا الحالة القاعية التي يكون الجسيم فيها ممتلكا أقل طاقة ممكنة له، وهي الحل عندما تكون .
مستوي الطاقة التالي هو المميز بحل معادلة شرودنجر عندما تكون ، ونلاحظ أن الدالة الموجية لها تتكون من طول موجة واحدة للجسيم.
وعندما يكتسب الجسيم طاقة فوق طاقته عندما يكون في الحالة يقفز إلى الحالة وهي تتميز هنا بأنها تتكون من موجة ونصف موجة.
هذا التفسير يوضح معنى كمومية الطاقة، فالجسيم يمكنه امتلاك طاقات منفصلة معينة تسمى طاقات ذاتية. ولا يمكن للجسيم امتلاك طاقة بينية بين مستويين للطاقة طبقا لحلول معادلة شرودنجر. وهذا فعلا ما نجده في الواقع من خصائص الذرات والجزيئات.
مستويات طاقة مسموحة[عدل]
تتطلب نظرية الكم أن تكون المستويات الطاقة التي يمكن أن يمتلكها جسيم في جهد يؤثر عليه أن تكون حلول معادلة شرودنجر لها قابلة للتنسيب للواحد. فبينما تعطي المعادلة التفاضلية حلولا مختلفة لطاقة الجسيم، يحتم شرط قابلية الحل للتوحيد أن تكون:
أي أن يكون الجسيم موجودا أينما كان بين مالانهاية إلى مالانهاية.
إجراء التوحيد على معادلة الجسيم يعطي حلولا ذات مستويات الطاقة منفصلة للجسيم:
, حيث تكون مساوية لعدد صحيح أو مساوية للصفر.
تمثل هذه المعادلة مستويات الطاقة المختلفة التي يمكن للجسيم امتلاكها في الجهد التوافقي، فإذا اعتبرنا n=1 تصبح:
وهذا هو المستوى القاعي لطاقة الجسيم، وعلاوة على ذلك فلا يمكن للجسيم في الجهد التوافقي أن تكون طاقته صفرا، وأنما أقل طاقة له هل نصف طاقته الذاتية حيث ثابت بلانك المخفض و التردد الذاتي للجسيم.
الطاقة عند الصفر المطلق[عدل]
تنبع من النتيجة السابقة نتيجة أساسية: لا يمكن للهزاز التوافقي اتخاذ طاقات تواصلية، وإنما يمكنه امتلاك اعدادا صحيحة من الطاقة . وتكون الحالة القاعية التي يمتلك فيها الهزاز التوافقي أقل طاقة على الإصلاق هي .
ومن تلك النتيجة نستنتج أن الهزاز التوافقي تكون له طاقة (يهتز) أيضا عند درجة الصفر المطلق ومقدارها هي الطاقة ، تلك هي نتيجة ميكانيكا الكم عند معالجتها للهزاز التوافقي على المستوى الذري.
أما في حالة التعامل مع تلك المسألة بالميكانيكا الكلاسيكية تكون درجة الحرارة مقياسا لطاقة الجسيم ولكل درجة من درجات حريته. وعند الصفر المطلق تقول الميكانيكا الكلاسيكية أن طاقة النظام تكون بالتالي مساوية للصفر. وهنا تقدم ميكانيكا الكم حلا مناقضا مع الحل الكلاسيكي، ورغم ذلك فإن الحل الذي تقدمة ميكانيكا الكم هو المتوافق فعلا مع وصف الطبيعة. ويتضح ذلك أيضا من أن احتمال وجود الجسيم في الموضع المميز يكون له اتساعا معينا وليس صفرا. معنى ذلك ان الجسيم لا يستقر موقعه في النقطة مثلما نتوقع من الحل الذي يقدمة الهزاز الكلاسيكي. وهذا الحل الذي تقدمه مكيكانيكا الكم يسمى اهتزاز درجة الصفر المطلق وبالتالي طاقة الصفر المطلق.

طاقة الصفر المطلق عن طريق مبدأ عدم التأكد[عدل]
يمكن وصف خاصية وجود طاقة للجسيم الموجود جهد توافقي بالاستعانة بمبدأ عدم التأكد ل هايزنبرج التي صاغها عام 1934 باستخدامه وتطويره لميكانيكا الكم. فطبقا للحالة الكلاسيكية التي تصفها الميكانيكا الكلاسيكية لنيوتن يتخذ الجسيم المهتز الوضع و وزخم الحركة . أما في ميكانيكا الكم فلا يمكن تحديد وضع مكان الجسيم بدقة كاملة وفي نفس الوقت تعيين زخم حركة الجسيم بدقة كاملة، وإنما تتحكم في دقة تعيين هذين الاثنين مبدأ عدم التأكد لهايزنبرج. أي يكون تعيين موضع الجسيم وزخم حركته محفوفا بدرجة من عدم التأكد. أي يمكن تخيل أن الجسيم لا يكون نقطيا وإنما في هيئة «سحابة» ذات أبعاد وتحمل أقل طاقة لها ممكنة.
بذلك يمكن تعيين موضع الجسيم وزخم حركته عند نقطة الصفر باستخدام مبدأ عدم التأكد كالآتي: أقل طاقة يمكن للجسيم امتلاكها ستتحكم فيه عدم التأكد في تعيين كلا من وضع الجسيم وزخم حركته، ويمكننا كتابة معادلة هاميلتون لتلك الحالة للهزاز:
وطبقا لعلاقة عدم التأكد يمكننا الآن حساب الطاقة E، فنحصل على:
وتكون الطاقة في أدنى مقدار لها عندما تكون ، أي عندما تكون
وهذا يعطينا:
حالة خاصة كلاسيكية[عدل]
في الحالة الخاصة عندما يتخذ العددالكمومي n مقاديرا كبيرة يتحول احتمال وجود الجسيم في المجال التوافقي كمومي إلى حالة احتمال وجوده في هزاز توافقي كلاسيكي (رقاص). ويكون احتمال وجود الجسيم متناسبا عكسيا مع سرعته 1/v، (احتمال وجود الجسيم عند نقطتي العودة من اليمين إلى اليسار أو من اليسار إلى اليمين تكون أكبر من تلك عند نقطة السكون الوسطية). وكلما انخفضت سرعة v الجسيم الكلاسيكي في المجال كلما زاد زمن بقائه عند النقطة المذكورة. ويمكن استنباط السرعة مباشرة من قانون بقاء الطاقة. ويبين الشكل الآتي كثافة احتمال وجود الجسيم في الحالتين الكلاسيكية والكمومية. كلما زادت n كلما اقترب التشابه بين المنحنيين: الحالة الكلاسيكية وحالة ميكاينيكا الكم.

حالات شبه كلاسيكية[عدل]

عندما نعتبر الجسيم كحزمة موجية فإنه يتصرف كما لو كان جسيما تحت تاثير جهد توافقي (لهذا نقول ان حالته هذه حالة كلاسيكية). فعندما يصطدم بحافة الجهد فإنه ينعكس عليه إلى الداخل. ويمارس بذلك تردده وأرجحته بين حافتي المجال. (يمكن تصور إلكترونا يتحرك في مجال النواة الذرية ويحصره المجال في حدود الشكل الموضح).
تسمى تلك الحالات في الرياضة حالات تناسقية موجية، وهي تمثل كعدد مركب α وتصف حالات النظام عن طريق عمليات جمع خطية :
تهمنا تلك الحالات عندما نصف موجات تناسقية، حيث يمكن بواسطها تعيين التوزيع المحتمل لها (مثلما يحدث عند إحصاء الفوتونات في تناسق موجات الضوء). ويكون التوزيع المحتمل في هيئة توزيع بواسون:
يمكن تصور الحالة شبه الكلاسيكية بجزيئ مكون من ذرتين مثل [[جزيئ الهيدروجين تسمى تلك الحالات في الرياضة حالات تناسقية موجية، وهي تمثل كعدد مركب α وتصف حالات النظام عن طريق عمليات جمع خطية :
تهمنا تلك الحالات عندما نصف موجات تناسقية، حيث يمكن بواسطها تعيين التوزيع المحتمل لها (مثلما يحدث عند إحصاء الفوتونات في تناسق موجات الضوء). ويكون التوزيع المحتمل في هيئة توزيع بواسون:
يمكن تصور الحالة شبه الكلاسيكية كجزيئ مكون من ذرتين مثل جزيئ الهيدروجين H2 حيث نثير اهتزازه بواسطة تصليت شعاع الليزر عليه. .[2] وقد وضحنا أعلاه أن اهتزاز جزيئ مكون من ذرتين يمكن وصفه بتقريب مقبول كهزاز توافقي. ويبين الشكل التالي ما يحدث لأحد الذرتين في الجزيئ:

سنسلط شعاع الليزر على إحدى الحزم الموجية (لإحدى الذرتين) أثناء وجودها في مستوي طاقة سفلي فيرفعها إلى مستوي طاقة أعلى. فتبقى في هذا المستوي لمدة زمنية ثم تبدأ الحركة في هيئة حالة شبه كلاسيكية في المجال. ولقياس طاقة تلك الحالة نصوب شعاعا ثانيا من الليزر يعمل على تأين الجزيئ. فيعطينا وضع الدالة الموجية المسافة بين الذرتين في الجزيئ. وبتعيين طاقة الحركة لجزئي الجزيئ المنفصلين يمكننا تعيين المسافة بينهما وتعيين شكل الحزمة الموجية.
المصادر[عدل]
- ^ M. Planck: Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum, Verhandlungen der Deutschen physikalischen Gesellschaft 2(1900) Nr. 17, S. 237 - 245, Berlin (vorgetragen am 14. Dezember 1900)
- ^ Th. Ergler, A. Rudenko, B. Feuerstein, et.al.: Time-Resolved Imaging and Manipulation of H2 Fragmentation Intense Laser Fields In: Phys. Rev. Lett. 95, 093001, 2005
انظر أيضاً[عدل]
| في كومنز صور وملفات عن: هزاز توافقي |






















































