مثلث متساوي القياس

المثلث متساوي القياس هو عندما يكون مع مثلث آخر تساوي قياس (انسحاب، دوران، تناظر، أو مركب لمثل هذه التحولات) يكون من خلاله صورة الآخر.

هذا يتوافق مع فكرة تداخل المثلثات. تأتي أهمية هذه الفكرة من حقيقة أنها تعكس شكلاً من أشكال التجانس في المستوى الإقليدي.^[1]

حالة المساواة[عدل]

الشروط الثلاثة التالية، تسمى حالات المساواة للمثلثات متكافئة :

التوصيف الأول[عدل]

يكون المثلثان متساوي القياس عندما يكون أطوال أضلاعهما اثنين في اثنين متساويين. يمكن إثبات أن مثلثين متساوي القياس هما في الواقع صورة لبعضهما البعض من خلال قياس تساوي المستوى.

التوصيف الثاني[عدل]

يكون المثلثان متساوي القياس عندما يكون لهما ضلع بنفس الطول بين زاويتين متماثلتين من نفس القياسات.

التوصيف الثالث[عدل]

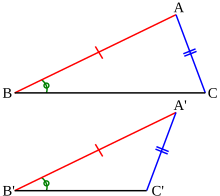
يكون المثلثان متساوي القياس عندما يكون لهما زاوية بنفس القياس بين ضلعين متماثلين من نفس الطول.

المظاهرات[عدل]

في إقليدس[عدل]

حالات المساواة بين المثلثات هي موضوع الدعامة. 4 و 7 و 8 و 26 من الكتاب الأول من عناصر إقليدس.

لتوضيح الحالة الثالثة، على سبيل المثال، يأخذ إقليدس في الاعتبار المثلثين ABC و DEF بحيث يكون الطول AB مساويًا لـ DE، والطول AC إلى DF والزاوية ${\widehat {BAC}}$ إلى ${\widehat {EDF}}$ . ثم يطبق المثلث ABC على المثلث DEF بحيث يتطابق A مع D، ونصف الخط [ AB ) مع نصف الخط [ DE ) . [ AB ] و [ DE ] لهما نفس الطول ويتزامن A مع D، ستتطابق النقطتان B و E. الزوايا ${\widehat {BAC}}$ و ${\widehat {EDF}}$ بالتساوي، فإن نصف الخط [ AC ) سوف يتطابق مع نصف الخط [ DF )، و [ AC ] و [ DF ] لهما نفس الطول، و C و F سيتطابقان.

في هيلبرت[عدل]

لم يكن حتى XIX قرن لمظاهرة إقليدس ليتم انتقادها. في الواقع، هذا يفترض وجود تحويل متساوي القياس يرسل [ AB ] على [ DE ]، يرسل آخر [ AC ] على [ DF ] وثالث يرسل الزاوية ${\widehat {BAC}}$ في الزاوية ${\widehat {EDF}}$ ، لكن الدليل يفترض أن هذه التحولات الثلاثة تشكل واحدة فقط. في عام 1899، في كتابه أسس الهندسة، يسلط ديفيد هيلبرت الضوء على صعوبة المشكلة من خلال عرض هندسة تختلف فيها التحولات الثلاثة والتي تكون فيها حالات تساوي المثلثات خاطئة.^[2] لذلك يعالج هلبرت حالات المساواة في المثلثات على النحو التالي. يعتبر فكرة التطابق (أو المساواة) بين المقاطع والزوايا بدائية ويعطي البديهيات التي تحكم هذه الفكرة. على وجه الخصوص، يجب أن تتعلق إحدى البديهيات بتطابق المقطع وتطابق الزاوية، وتتكون هذه البديهية من الحالة الثالثة للمساواة بين المثلثات. لذلك لم تعد هذه القضية نظرية لهيلبرت. بمجرد القيام بذلك، تمكن هيلبرت من استنتاج حالات المساواة الأخرى.

مظاهرة حديثة[عدل]

عادة تستخدم حقيقة أن طول المقاطع وقياس الزوايا يتم التعبير عنها عن طريق المنتج العددي، وأن المقاييس المتساوية تحافظ على الناتج العددي. بالنظر إلى المثلثين ABC و DEF، نحدد خريطة أفينية فريدة ترسل A إلى D و B إلى E و C إلى F. إن فرضيات الحالات المختلفة لتساوي المثلثات تجعل من الممكن إظهار أن هذه الخريطة هي قياس متساوي.

انظر أيضا[عدل]

مراجع[عدل]

^ روبن هارتشورن (2000). [مثلث متساوي القياس، صفحة. 148, في كتب جوجل Geometry, Euclid and Beyond] (بالإنجليزية). Springer. p. 148. ISBN:978-0-387-22676-7. {{استشهاد بكتاب}}: تحقق من قيمة |مسار= (help).
^ David Hilbert, Les fondements de la géométrie, Dunod (1971), rééd. Gabay (1997), annexe II.

مثلث متساوي القياس في المشاريع الشقيقة:

صور وملفات صوتية من كومنز.

[1] روبن هارتشورن (2000). [مثلث متساوي القياس، صفحة. 148, في كتب جوجل Geometry, Euclid and Beyond] (بالإنجليزية). Springer. p. 148. ISBN:978-0-387-22676-7. {{استشهاد بكتاب}}: تحقق من قيمة |مسار= (help).

[2] David Hilbert, Les fondements de la géométrie, Dunod (1971), rééd. Gabay (1997), annexe II.

[1]

[2]