في الهندسة الرياضية، تقوم معادلة براهماغوبتا بإيجاد مساحة أي رباعي أضلاع بواسطة طول أضلاعه وقياس بعض زواياه.[1]
بشكلها الأكثر شيوعاً تقوم المعادلة بحساب معادلة رباعي الأضلاع المحصور ضمن دائرة (رباعي دائري).
الصيغة البسيطة[عدل]
أبسط صيغة لصيغة براهماغوبتا هي الصيغة التي تعطى في الرباعي الدائري الذي أطوال أضلاعهa, b, c, d على الشكل التالي:

حيث s تعطى بالعلاقة: 
وهي تعميم لمعادلة هيرون لحساب مساحة المثلث.
البرهان[عدل]
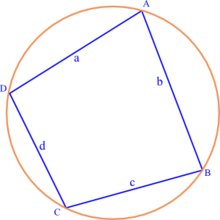
لتكن  هي مساحة الرباعي جانبه.
هي مساحة الرباعي جانبه.  هي مجموع مساحتي المثلثين
هي مجموع مساحتي المثلثين  و
و  إذن
إذن

بما أن  رباعي دائري فإن ∠DAB = 180° − ∠DCB و منه فإن sin A = sin C، و منه:
رباعي دائري فإن ∠DAB = 180° − ∠DCB و منه فإن sin A = sin C، و منه:  .
.
إذن 
بتطبيق قانون جيب التمام نستنتج أن:

نعوض cos C = −cos A، لدينا 
نعوض في متساوية المساحة،




نأخذ  ، فنجد
، فنجد


انظر أيضاً[عدل]
مراجع[عدل]
وصلات خارجية[عدل]
إيريك ويستاين، معادلة براهماغوبا، ماثوورلد Mathworld (باللغة الإنكليزية).



















