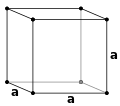
نظام بلوري مكعب


النظام البلوري المكعب في علم المعادن هو أحد أنظمة تبلور المعادن. وجد عمليا أن الأملاح والمعادن تتبلور طبقا لأحد 7 أنظمة للتبلور. منها النظام بلوري الثلاثي ونظام بلوري الرباعي أو نظام بلوري أحادي الميل، وأكثر تلك الأنظمة شيوعا وأبسطها هو النظام البلوري المكعب.
توجد من النظام المكعب ثلاثة أنواع مختلفة ،وهي المكعب البسيط، والمكعب مركزي الجسم والمكعب مركزي الوجه.
- ويتسم نظام المكعب البسيط باحتوائه على ذرة واحدة في وحدة الخلية.
- ويتسم نظام المكعب مركزي الجسم باحتواء وحدة خليته ذرتين،
- ويتسم نظام المكعب مركزي الوجه باحتواء وحدة خليته 4 ذرات (أنظر الشكل).
يتبلور الحديد طبقا لنظام المكعب مركزي الجسم، ويتبلور النحاس طبقا لنظام المكعب مركزي الأوجة.
شبكات تبلور برافيه للمكعب[عدل]
تساعد شبكة تبلور برافيه على دراسة التركيب بصفة عامة، ونستغلها هنا لدراسة الثلاثة أنظمة للمكعب:
-
مكعب البسيط(P)
-
مكعب مركزي الجسم(I)
(ذرة تشغل المركز) -
مكعب مركزي الوجه(F)
يشغل المكعب البسيط ذرة على الشبكة البلورية ذات الثلاثة محاور: كل ركن من أركان المكعب الثمانية تشغلها ذرة ، تكون مشتركة بين 8 مكعبات مجاورة، وعلى ذلك فكل وحدة خلية تشغلها ذرة واحدة (1/8 × 8).
بالنسبة إلى نظام المكعب مركزي الجسم (body-centered cubic (I نجد أن وسط الخلية تشغله ذرة إضافية ، وبذلك تكون وحدة خلية المكعب مركزي الجسم مشغولة بذرتين اثنتين (1/8 × 8 + 1). من هذا النوع نجد الحديد يتبلور على هذه الصورة .
أما النحاس مثلا فهو يتبلور بهيكل آخر ، وهو نظام المكعب مركزي الوجهface-centered cubic (F) : في ذلك المكعب تشغل ذرة كل وجه من الستة أوجه للمكعب ، وكل واحدة منها يتقاسمها مكعبان متجاوران، فيكون عدد الذرات الموجودة في وحدة الخلية للمكعب مركزي الوجه 3 ذرات من الأوجه بالإضافة إلى ذرة تشغل نقاط الشبكة (الأركان)، فيكون المجموع 4 ذرات للمكعب مركزي الوجه ((1/8 لكل ركن) × 8 أركان + (1/2 لكل وجه) × 6 أوجه).
النظام الرباعي المركزي :
-
النظام الرباعي المركزي
في النظام الرباعي المركزي ، تشغل ذرة وسط وحدة الخلية مع استطالة الاضلاع الرأسية للخلية . وهو يسمى الضلع c الذي يختلف طوله عن طول الضلع a.
معامل شغل الخلية[عدل]
من خواص التبلور يهم معدل شغل الخلية ، أي الاقتصادية في شغل فراغ الخلية بملئها بأكبر عدد ممكن من الذرات . ولا يمكن ذلك إلا بأخذ طبيعة الذرات من حيث الحجم واتجاه روابطها. ولكن لتبسيط الأمر يمكننا اعتبار أن الذرات في البناء البلوري متماثلة الحجم وأن كل منها كروي الشكل، وأن يكون نصف قطر كل منها كافيا لملامسة جاره، فيكون معامل شغل الخلية هو نسبة شغل فراغ الخلية بالذرات أو بتلك الكرات.
نجد في حالة المكعب البسيط ذو الضلع a أن نصف قطر الكرة يبلغ a⁄2 ويبلغ معامل شغل الخلية 0.524(وهذا معدل صغير). وإذا اعتبرنا وحدة خلية المكعب مركزي الجسم BCC lattice، نجد معدل شغل الخلية قد زاد إلى 0.680 . ويصل معدل شغل الخلية أقصاه في حالة المكعب مركزي الوجه FCC حيث يصل ذلك المعدل 0.740 . أي أن نظام المكعب مركزي الوجه هو نظريا أعلى معدل شغل لفراغ الخلية عند التبلور. كما يصل إلى نفس المعدل النظام البلوري السداسي ذو ذرة بوسطه hexagonal close packed وكذلك النظام الرباعي مركزي الجسم.
وطبقا للقاعدة أن ذرات المادة تتجاذب فيمكن توقع أن يشغلوا الخلايا إلى أقصى حد ممكن وأن تشكل الأنظمة ذات معدل عال لشغل فراغ الخلية هي الأغلبية. وهي الواقع هذا هو ما نجده عمليا. فنجد نظام المكعب البسيط نادرا في الطبيعة نظرا لعدم استغلاله لفراغ الخلية على الوجه الأمثل، ومثال على ذلك نجده في بلورة البولونيوم. وعلى العكس نقابل النظامين مركزي الجسم ومركزي الوجه كثيرا في المعادن، فبالنسبة للمكعب مركزي الجسم نجد أمثلة الحديد والكروم والتنجستن والنيوبيوم . ويتمثل المكعب المركزي الوجه في الرصاص ونترات الرصاص والألمونيوم والنحاس والذهب والفضة.
مؤشرات ميلر[عدل]

يمكن وصف المتجهات والمستويات المتماثلة للذرات في البلورة بواسطة ثلاثة قيم تسمى مؤشرات ميلر . وتعني كل من l وm وn مؤشرات للاتجاهات الثلاثة المعتادة وهم متعامدين على بعضهم البعض.
وتعرف القيمة أحد المستويات المقطعية في البلورة، فكل ثلاث نقاط تقاطع و و , في البلورة أو مضاعفات لها تعبر عن مستوى معين في البلورة . أي أن مؤشرات ميلر تتناسب تناسبا طرديا مع معكوسات نقاط تقاطع مستوي معين مع متجهات أضلاع a وحدة الخلية. فإذا كانت إحدى مؤشرات ميلر = 0 ، فهذا يعني أن المستوي لا يتقاطع مع ذلك الضلع أو المحور ،أي يقابله في مالا نهاية.[1]
وبالأخذ في الاعتبار المستويات التي تقطع نقطة واحدة أو أكثر على الشبكة البلورية فقط، فيمكن حساب المسافة العمودية dالفاصلة بين مستويين من نفس النوع بواسطة العلاقة:
تفسير المستويات الموجودة في الشكل[عدل]
1. المستوي (001) :
- L = 0 المستوي لا يتقاطع مع المحور L ،
- m = 0 المستوي لا يتقاطع مه المحور m ،
- n = 1 المستوي يتقاطع مع المحور n عند a.
لهذا يسمى المستوي الرمادي (001).
2. المستوي (111) :
- L = 1 المستوي يقطع المحور L عند L = a،
- m = 1 المستوي يقطع المحور m عند m = a،
- n = 1 المستوي يقطع المحور n عند n = a.
لذلك فالمستوي المعني هو (111).
- وإذا افترضنا أن طول ضلع وحدة الخلية a = 1,2 أنغستروم أمكننا حساب المسافة العمودية d بين المستويات [110] أو المستويات [100].
بلورة أحادية Monocrystaline[عدل]

بلورة أحادية (بالإنجليزية:single crystal ) هي مادة صلبة تتميز بامتداد الشبكة البلورية فيها من أولها إلى آخرها مكونة بلورة كبيرة منتظمة. وتتكون البلورة الأحادية مثلا عن طريق تغطيس بلورة صغيرة في محلول مشبع بمادة البلورة، وتكون البلورة الصغيرة بمثابة بذرة تتراص عليها الذرات أو الجزيئات، وتأخذ كل ذرة من ذرات المذاب موضعها بالضبط في الشبكة البلورية وبذلك تنمو البذرة إلى بلورة أحادية كبيرة.
متعددة البلورات Polycrystaline[عدل]

متعددة البلورات (بالإنجليزية: Polycrystalline) هي مواد مكونة من حبيبات بلورية كثيرة لها أحجام مختلفة وعشوائية التوزيع. يمكن عن طريق ضبط عملية التبلور التوصل إلى تقليل عشوائية التوزيع بحيث تنتظم البنية البلورية ونحصل على ما يسمى بلورة أحادية.
- تبين الصورة المجاورة تكون الحديد الصلب من حبيبات ، تشكل كل منها بلورة أحادية تتبع النظام البلوري الخاص بالحديد، وتتوزع فيه البلورات الأحادية توزيعا عشوائيا بالنسبة للاتجاه.
وتعتبر معظم المعادن وخزف موادا كثيرة البلورات ، وكثيرا ماتسمى البلورات الأحادية الصغيرة فيها بالحبيبات. ويمكن تصور كثيرة البلورات عند طحن بلورة أحادية، فكومة المسحوق تشكل مادة كثيرة البلورات.
اقرأ أيضا[عدل]
- وحدة خلية
- نظام بلوري
- شبكة تبلور برافيه
- نظام بلوري رباعي
- نظام بلوري سداسي
- بنية الألماس المكعبة
- علم البلورات
- بنية بلورية
- محلول جامد
المراجع[عدل]
- ^ Neil W. Ashcroft and N. David Mermin, Solid State Physics (Harcourt: New York, 1976)
| في كومنز صور وملفات عن: نظام بلوري مكعب |