قرص مزود

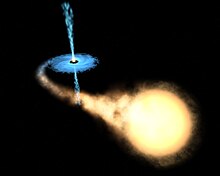
القرص المُزوِّد أو التراكمي [1] في الفلك (بالإنجليزية:accretion disc) هو نوع من الأقراص النجمية الدوارة وهو عبارة عن حزام من الغاز والغبار الكوني يحيط بنجم في طور التكوين (نجم أولي)غالباً، لكن من الممكن أن يكون القرص حول قزم أبيض أو نجم نيوتروني أو ثقب أسود ويدور حوله بفعل الجاذبية. جاءت تسميته القرص التراكمي من أنه يٌمد نجمه باستمرار بالمادة وهذا ما يساعد النجم على زيادة كتلته. تزداد كتلة النجم بما يتراوح بين 10−7 و10−9 كتلة شمسية في السنة. تصدر الأقراص حول النجوم الشابة أو النجوم الأولية موجات الأشعة تحت الحمراء وبواسطة رصدتلك الأشعة نتعرف على تلك النجوم الناشئة، أما عندما تكون الأقراص حول نجم نيوتروني أو ثقب أسود فهي تصدر أشعة سينية عالية الطاقة، ذلك لأن الثقب الأسود والنجم النيوتروني شديدة الانضغاط وعالية الكثافة وبالتالي جاذبيتها تكون عالية جدا؛ تتساقط عليها المادة بسرعات رهيبة فتصدر المادة أشعة سينية.
حركة التزويد[عدل]
يدور قرص من الغاز والغبار حول الجسم المركزي ليس بسرعة متساوية وإنما تختلف السرعات للغاز في الجزء الداخلي من القرص عن سرعة الأجزاء في الأطراف. وطبقا قوانين كبلر تدور أجزاء الغاز القريبة من الجسم المركزي أسرع وينتج عن ذلك احتكاك بين جزيئات الغاز وبعضها. ينتج بالتالي عن هذا الاحتكاك تكون الدوامات وتصادم بين الجسيمات وتسقط بعضها بفعل الجاذبية على الجسم المركزي، بذلك تزداد كتلة الجسم المركزي شيئا فشيئا.
أثناء تلك العملية فالجسيم لا بد وأن ينقل زخمه الزاوي إلى الخارج طبقا لقانون انحفاظ الزخم الزاوي، ويتم ذلك باعطائه زخمه الزاوي لأحد الجسيمات في القرص فيتخذ الجسيم المكتسب للزخم الزاوي مدارا أكبر في القرص مبتعدا عن الجسم المركزي. (هذا أحد تفسيرات تكون أذرعة حلزونية للمجرات حول حوصلة مجرة).
وإذا كان الغاز في القرص قليل التأين فتنشأ عن حركة الأيونات مجالات مغناطيسية تؤثر على حركة الأيونات. وتختلط تأثيرات المغناطيسية الدوارة مع الاحتكاكات الناتجة من الدوامات مما يجعل بعض الجسيمات يسقط على الجسم المركزي وتزيد من كتلته. والنظرية التي تصف حركة البلازما في مجال مغناطيسي نجدها في ديناميكا الموائع المغناطيسية.
نشأة قرص مزود[عدل]
نشاهد وجود القرص المزود حول النجم الناشئ (يجمع النجم بذلك مادة من القرص ويزيد من كتلته). وكذلك نجد القرص حول النجوم الزائفة وحول الثقوب السوداء. كذلك نشاهدها حول أجرام أخرى ندرسها في علم الفلك، مثل حلقات زحل المتكونة من جليد.
ونشاهدها في أجرام منضغطة مثل نجوم نيوترونية وحول ثقب أسود حيث يكفي اكتسابها لطاقة وضع عالية ناتجة عن جاذبية الجسم المركزي التي تؤلق القرص. بهذه الطريقة وبحسب شدة الاحتكاك بين الجسيمات فيمكن أن تصدر موجات كهرومغناطسية عالية الطاقة مثلما تنتج من تفاعلات نووية. وهذا ما يفسر شدة الضياء العالية التي نشاهدها في النجوم الزائفة والتي نراها على الرغم من بعدها الشاسع عنا.
نموذج قرص ألفا[عدل]
افترض كل من نيقولاي شاكورا وراشد سونيايف عام 1973 .[2][3] أن دوامات تحدث للغاز في القرص تكون مصدرا لزيادة اللزوجة. وبافتراض أن الدوامات تحدث عند سرعات تحت سرعة الصوت واعتبار أن سمك القرص هو أقصي حد لحجم الدوامات فيمكن حساب اللزوجة من المعادلة الآتية:
حيث:
ارتفاع القرص
معامل يساوي صفر (في حالة عدم وجود تزويد) أو 1.
مع اعتبار أن الحركة الدوامية تعادل:
حيث:
سرعة الخلية الدوامية بالنسبة للسرعة المتوسطة للغاز،
حجم أكبر خلية دوامية، وتصفها الصيغتان:
- و ,
حيث السرعة الزاوية طبقا لقانون كبلر تساوي:
و نصف قطر المدار حول الجسم المركزي. [4]
وباستخدام معادلة التوازن الهيدروستاتيكي وأخذ انحفاظ الزخم الزاوي في الاعتبار، وافتراض أن سمك القرص رفيع فيمكن حل معادلات شكل القرص بواسطة المعامل .
وباستخدام قانون كرامر، نحصل على:
حيث:
و هما درجة حرارة وكثافة الخط الوسطي،
معامل التزويد محسوبا بالوحدة ,
كتلة الجسم المركزي بوحدات كتلة شمسية ,
نصف قطر مدار نقطة على القرص بالوحدة ,
و
,
حيث:
نصف القطر الذي عنده يتوقف الزخم الزاوي من الدخول نحو المركز.
ويعتبر نموذج قرص ألفا المحسوب طبقا للعالمين شاكورا وسونياف غير مستقر من الوجهتين الحرارية واللزوجة.
- وتُعرف طريقة أخرى للحساب تعتمد على نموذج قرص بيتا وتؤدي إلى استقرار القرص بالنسبة للزوجته وحرارته مع اعتبار اللزوجة تتناسب مع ضغط الغاز .
يلاحظ أن النموذج الأساسي لشاكورا وسونيايف يعتبر اللزوجة تتناسب تناسبا طرديا مع الضغط الكلى للغاز، أي أن:
حيث:
ويعتبر نموذج شكورا وسونيايف أن القرص يكون في توازن حراري ويستطيع إشعاع حرارته بكفاءة. وفي تلك الحالة يشع القرص حرارة اللزوجة فيبرد ويصبح سمكه رفيعا. ولكن هذا الافتراض قد لا يسري، ففي حالة عدم كفاءة القرص على اشعاع الحرارة فقد ينتفخ القرص في هيئة إطار أو في شكل آخر ليس مسطحا له بعدين ولكن حجميا ذو ثلاثة أبعاد. ولكن الحل الذي ينتج شكل الإطار يتطلب أن يكون معدل التزايد أقل قليلا من حد إدنجتون.
- ونموذج ثالث يماثل حلقات زحل حيث يكون القرص فقير الغاز بحيث يكون انتقال الزخم الزاوي
بصفة أساسية عن طريق تصادمات بين حبيبات صلبة وتفاعلات الجاذبية بين القرص وقمر. هذا النموذج يتطابق مع قياسات فلكية أجريت خلال السنوات القليلة الماضية بطريقة عدسات الجاذبية .[7] [8] [9] .[10]
اقرأ أيضا[عدل]
- قرص كوكبي
- سديم كوكبي
- قائمة أكبر النجوم
- ثقب أسود فائق الضخامة
- قائمة أكبر النجوم كتلة
- قائمة أشد النجوم سطوعا
- قائمة انفجارات أشعة غاما
مراجع[عدل]
- ^ ناسا بالعربي - لأول مرة على الإطلاق، العلماء يرصدون كواكب خارج مجرتنا نسخة محفوظة 14 فبراير 2019 على موقع واي باك مشين.
- ^ Shakura، N. I.؛ Sunyaev، R. A. (1973)، "Black Holes in Binary Systems. Observational Appearance"، Astronomy and Astrophysics، ج. 24، ص. 337–355، Bibcode:1973A&A....24..337S
- ^ Weizsäcker، C. F. (1948)، "Die Rotation Kosmischer Gasmassen"، Z. Naturforsch.، ج. 3a، ص. 524–539
- ^ Landau and Lishitz (1959)، Fluid Mechanics (ط. 31)
- ^ Lightman and Eardley، Alan P.؛ Eardley، Douglas M. (1974)، "Black Holes in Binary Systems: Instability of Disk Accretion"، The Astrophysical Journal,، ج. 187، ص. 1، Bibcode:1974ApJ...187L...1L، DOI:10.1086/181377
{{استشهاد}}: صيانة الاستشهاد: علامات ترقيم زائدة (link) - ^ Piran، T. (1978)، "The role of viscosity and cooling mechanisms in the stability of accretion disks"، The Astrophysical Journal,، ج. 221، ص. 652، Bibcode:1978ApJ...221..652P، DOI:10.1086/156069
{{استشهاد}}: صيانة الاستشهاد: علامات ترقيم زائدة (link) - ^ Poindexter، Shawn؛ Morgan، Nicholas؛ Kochanek، Christopher S.؛ وآخرون (2008)، "The Spatial Structure of An Accretion Disk"، The Astrophysical Journal,، ج. 673، ص. 34، arXiv:0707.0003، DOI:10.1086/524190
{{استشهاد}}: Explicit use of et al. in:|الأخير=(مساعدة)صيانة الاستشهاد: علامات ترقيم زائدة (link) - ^ Eigenbrod؛ وآخرون (2008)، "Microlensing variability in the gravitationally lensed quasar QSO 2237+0305 = the Einstein Cross. II. Energy profile of the accretion disk"، Astronomy & Astrophysics,، ج. 490، ص. 933، arXiv:0810.0011
{{استشهاد}}: Explicit use of et al. in:|الأخير=(مساعدة)صيانة الاستشهاد: علامات ترقيم زائدة (link) - ^ Mosquera، A. M.؛ Muñoz، J. A.؛ Mediavilla، E.؛ وآخرون (2009)، "Detection of chromatic microlensing in Q 2237+0305 A"، The Astrophysical Journal,، ج. 691، ص. 1292، arXiv:0810.1626، DOI:10.1088/0004-637X/691/2/1292
{{استشهاد}}: Explicit use of et al. in:|الأخير=(مساعدة)صيانة الاستشهاد: علامات ترقيم زائدة (link) - ^ Floyd؛ وآخرون (2009)، "The accretion disc in the quasar SDSS J0924+0219"، ArXiv:0905.2651v1 [astro-ph.HE]، arXiv:0905.2651
{{استشهاد}}: Explicit use of et al. in:|الأخير1=(مساعدة)
| في كومنز صور وملفات عن: قرص مزود |
























![{\displaystyle f=\left[1-\left({\frac {R_{\star }}{R}}\right)^{1/2}\right]^{1/4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e053781dbfdf610a0e7cfead8b17c202f83f0f6)



