قانون فاراداي

| جزء من سلسلة مقالات حول |
| الكهرومغناطيسية |
|---|
 |
| بوابة كهرومغناطيسية |
قانون فاراداي[2] أو قانون فاراداي للحث الكهرومغناطيسي هو قانون أساسي في الكهرومغناطيسية والذي يتنبأ بطريقة تفاعل الحقل المغناطيسي مع التيار الكهربائي لينتج قوة دافعة كهربائية في ظاهرة تسمى الحث الكهرومغناطيسي وهي المبدأ الرئيسي للمحول والمحث والعديد من أنوع المحركات الكهربية والمولدات والملفات الكهربائية.[3][4]
معادلة ماكسويل فاراداي هي تعميم لقانون فاراداي وهي أحد معادلات ماكسويل.
التاريخ[عدل]

تم اكتشاف الحث الكهرومغناطيسي بشكل مستقل بواسطة مايكل فاراداي في عام 1831 وجوزيف هنري في عام 1832.[5][6][7] كان فاراداي هو أول من نشر نتائج تجاربه. في أولى تجارب فاراداي للحث الكهرومغناطيسي (29 أغسطس1831)[8] قام فاراداي بلف سلكين حول جانبين مختلفين من حلقة حديدية. وبناء على تقييمه لخواص المغناطيسات الكهربية المكتشفة حديثا، توقع فاراداي أنه عندما يبدأ التيار في السريان في أحد السلكين فإن نوعا ما من الموجات سينتقل خلال الحلقة مسببا تأثيرا كهربيا على الناحية المقابلة. قام بتوصيل أحد السلكين بجلفانوميتر وراقبه بينما وصل السلك الآخر ببطارية. بالفعل رأى تيارا مؤقتا (والذي أطلق عليه «موجة كهربية») عندما وصل السلك بالبطارية ولاحظ تيارا آخر عند فصل السلك عن البطارية.[9] سبب هذا الحث هو الاختلاف في التدفق المغناطيسي الذي حدث عند توصيل وعند فصل البطارية. في غضون شهرين كان فاراداي قد دون مجموعة أخرى من الملاحظات بخصوص الحث الكهرومغناطيسي. على سبيل المثال فقد لاحظ تيارات مؤقتة عندما يحرك قضيبا مغناطيسيا بسرعة داخل وخارج الأسلاك، وقام بتوليد تيارا ثابتا (تيار مستمر) عن طريق دوران حلقة نحاسية قرب قضيب مغناطيسي.[10]
شرح مايكل فاراداي الحث الكهرومغناطيسي مستخدما مبدأ أسماه خطوط القوة. إلا أن العلماء في ذلك الوقت رفضوا أفكاره النظرية بشكل واسع بسبب أنه لم يكن قد شكلها في صورة رياضية بعد.[11] الاستثناء كان جايمس كليرك ماكسويل والذي في 1861-1862 استخدم أفكار فاراداي كأساس لنظريته الكمية الكهرومغناطيسية.[11][12][13]
يصف قانون لينز والذي صاغه إيميل لينز في عام 1834[14] «التدفق خلال دائرة كهربية» كما يعطي اتجاه القوة الكهرومغناطيسية المستحثة والتيار الناتج عن الحث الكهرومغناطيسي.[15]
قانون فاراداي[عدل]
النص الكيفي[عدل]
ينص الإصدار الأكثر انتشارا لقانون فاراداي على:
تتناسب القوة الدافعة الكهربية المستحثة في أي دائرة مغلقة والمتولدة في ملف أو موصل طرديا مع المعدل الزمني الذي يقطع فيه الموصل لخطوط الفيض المغناطيسي.[16][17]
هذا الإصدار من قانون فاراداي يعمل فقط في دائرة مغلقة وعندما تكون الأسلاك رفيعة للغاية ولا يعمل في الظروف الأخرى والتي ستُناقش في الأسفل. الإصدار الآخر (معادلة ماكسويل فاراداي) والتي ستُناقش في الأسفل تعمل في كل الظروف.
النص الكمي[عدل]
يستخدم قانون فاراداي للحث الكهرومغناطيسي التدفق المغناطيسي ΦB خلال سطح افتراضي Σ ومحدود بدائرة مغلقة. ولأن الدائرة المغلقة قد تتحرك فقط كتب فاراداي Σ(t) للسطح. يمكن تعريف التدفق المغناطيسي عن طريق التكامل السطحي:
حيث dA هو عنصر مساحة السطح للسطح المتحرك Σ(t) وB هو المجال المغناطيسي (يطلق عليه أيضا «كثافة التدفق المغناطيسي»)، و B•dA هو متجه الضرب النقطي.
عندما يتغير التدفق المغناطيسي (لأن B اختلف أو لأن الدائرة الكهربية تحركت أو للسببين معا) يقول قانون فاراداي للحث الكهرومغناطيسي أن الدائرة الكهربية تكتسب قوة دافعة كهربية ℰ يمكن تعريفها بأنها الطاقة المتاحة من وحدة الشحنة والتي سافرت مرة خلال دائرة كهربية. بشكل متساو فهي فرق الجهد الكهربائي والذي يمكن قياسه عن طريق قطع السلك لتكوين دائرة مفتوحة وتوصيل الفولتميتر بسلك التوصيل.
ينص قانون فاراداي على أن القوة الدافعة الكهربية الناتجة تعتمد أيضا على معدل التغير في التدفق المغناطيسي:
حيث هي القوة الدافعة الكهربية وΦB هو التدفق المغناطيسي.
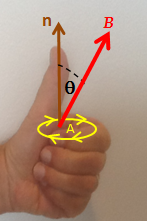
يحدد اتجاه القوة الدافعة الكهربية قانون لينز. إلا أنه يمكن تحديد اتجاه القوة الدافعة الكهربية مباشرة من قانون فاراداي دون استخدام قانون لينز باستخدام قاعدة اليد اليسرى[18] والتي تنص على التالي:
- قم بمحازاة الأصابع الملتفة لليد اليسرى مع الدائرة الكهربية (الدائرة الصفراء).
- قم بمد الإبهام. يشير الإبهام الممدود إلى الاتجاه س (البني) وهو المساحة المغطاة بالدائرة الكهربية.
- قم بإيجاد إشارة ΔΦB أو التغير في التدفق المغناطيسي. قم بتحديد التدفق الأولي والتدفق النهائي (والفارق بينهما ΔΦB) بالنسبة إلى المساحة س والمتحددة من الإبهام الممدود.
- إذا كان التغير في التدفق ΔΦB موجب الإشارة فإن الأصابع الملتفة تشير إلى اتجاه القوة الدافعة الكهربية (الدائرة الصفراء).
- إذا كان التغير في التدفق سالب الشحنة يكون اتجاه القوة الدافعة الكهربية معاكسا لاتجاه الأصابع الملتفة (عكس اتجاه أسهم الدائرة الصفراء).[19][20]
معادلة ماكسويل فاراداي[عدل]
معادلة ماكسويل فاراداي هي تعديل وتعميم لقانون فاراداي والتي تنص على أن المجال المغناطيسي المتغير مع الوقت سيكون دائما مصاحبا لمجال كهربائي متغير والعكس صحيح. معادلة ماكسويل فاراداي هي:
معادلة ماكسويل فاراداي هي واحدة من معادلات ماكسويل الأربعة ولذا فهي تلعب دورا هاما في النظرية الكهرومغناطيسية الكلاسيكية. يمكن أيضا كتابة المعادلة بطريقة تكاملية عن طريق نظرية كيلفن ستوك كالتالي:[21]
حيث:
- Σ هي المساحة المقطوعة بالشكل المغلق ∂Σ
- E هو المجال الكهربي وBهو المجال المغناطيسي
- dl هو عنصر متجه متناهي الصغر للشكل المغلق ∂Σ
- dA هو عنصر متجه متناهي الصغر للمساحة Σ.
إثبات قانون فاراداي[عدل]
معادلات ماكسويل الأربعة (ومنهم معادلة ماكسويل فاراداي) بالإضافة إلى قانون لورنتس هم أساس كاف لاستخلاص كل شئ في الكهرومغناطيسية الكلاسيكية. ولذا فإنه من الممكن إثبات قانون فاراداي بداية من هذه المعادلات.[22][23][24][25]
نقطة البداية هي التدفق المتغير مع الوقت في خلال مساحة تخيلية متحركة في الفضاء Σ:
طبقا للتعريف فإن كل هذا التدفق المتغير مع الوقت يمكن قياسه وتبسيطه بمساعدة معادلة ماكسويل فاراداي وقانون جاوس المغناطيسي وبعض المتجهات التكاملية. النتيجة هي:
حيث ∂Σ هي حدود المساحة Σ وvl هي سرعة حدود هذه المساحة.
في حين أن هذه المعادلة صحيحة لأي مساحة متحركة افتراضية Σ في الفضاء، إلا أنه يمكن تبسيطها أكثر في حالة خاصة عندما يكون ∂Σ دائرة مغلقة من الأسلاك. في هذه الحالة يمكننا أن نساوي بين الجهة اليمنى للمعادلة وبين القوة الدافعة الكهربية. بشكل خاص يمكن تعريف القوة الدافعة الكهربية بأنها الطاقة المتاحة لوحدة الشحنة التي تسافر مرة واحدة خلال دائرة كهربية مغلقة. لذا وطبقا لقانون لورنتس فإن:
حيث هي القوة الدافعة الكهربية وvm هي السرعة المادية أي سرعة الذرات المكونة للدائرة الكهربية ولذا فإن كانت ∂Σ هي الدائرة الكهربية المغلقة فإن vm=vl ومن هنا:
التطبيقات[عدل]
قانون فاراداي للحث الكهرومغناطيسي هو الأساس لعمل للعديد من التطبيقات مثل:
- المحول: وهو جهاز في الهندسة الكهربائية، مؤلف من ملفين من الأسلاك المنفصلة الملفوفة حول قضبان حديدية فقط بمسافة بسيطة، يسمى الطرف المرتبط بالمولد الكهربي بالملف الابتدائي بينما يطلق على الطرف المرتبط بالحمل مسمى الثانوي، ويستخدم المحول لتغيير قيمة الجهد الكهربي في نظام نقل الطاقة الكهربائية الذي يعمل على التيار المتردد حيث لا يمكن أن يعمل المحول في أنظمة التيار المستمر.[26][27]
- المحث: وهو أحد الادوات الإلكترونية أو الدارات التي من شأنها زيادة تدفق سيل التيار في دائرة الموصل. وهو يستخدم لتقليل التيار الكهربائي نوعا ما بحيث يتناسب التيار الذي يدخل الجهاز مع معدل صرفه.[28]
- المولد الكهربائي: هو جهاز ميكانيكي يحول الطاقة الحركية إلى طاقة كهربائية بوجود مجال مغناطيسي.[29]
- المحرك الكهربائي: هو آلة تحوِّل الطاقة الكهربائية إلى طاقة حركة دورانية لإنجاز شغل. وتُستَخدم المحركات الكهربائية لتشْغيل عدة آلات كهربائية ومعدات ميكانيكية مثل غسالات الملابس وأجهزة التكييف والمكانس الكهربائية ومجفِّفات الشعر وآلات الخياطة والمثاقب الكهربائية والمناشير. وتشغل أنواعٍ شتى من المحركات في القطارات والمترو وحافلات النقل العام الكهربائية (تروليباص)، كما تدير آلات المصانع والروبوتات.[30][31]
انظر أيضا[عدل]
مراجع[عدل]
- ^ Magnetism and Electricity A Manual for Students in Advanced Classes (بالإنجليزية). Longmans, Green, & Company. 1892. Archived from the original on 2021-02-27.
- ^ [أ] عمر شابسيغ؛ أميمة الدكاك؛ نوار العوا؛ هاشم ورقوزق (2016)، معجم مصطلحات الهندسة الكهربائية والإلكترونية والاتصالات (بالعربية والإنجليزية)، دمشق: مجمع اللغة العربية بدمشق، ص. 72، QID:Q108405620
[ب] مظهر طايل (1990)، قاموس الإلكترونيات الحديثة: إنكليزي - عربي (بالعربية والإنجليزية)، بيروت: دار الراتب الجامعية، ص. 181، OCLC:1103736455، QID:Q125527191
- ^ Sadiku، M. N. O. (2007). Elements of Electromagnetics (ط. 4th). New York & Oxford: Oxford University Press. ص. 386. ISBN:0-19-530048-3. مؤرشف من الأصل في 2016-12-02.
- ^ "Applications of electromagnetic induction". جامعة بوسطن. 22 يوليو 1999. مؤرشف من الأصل في 2018-06-30.
- ^ "A Brief History of Electromagnetism" (PDF). مؤرشف من الأصل (PDF) في 2017-12-15.
- ^ Ulaby، Fawwaz (2007). Fundamentals of applied electromagnetics (ط. 5th). Pearson:Prentice Hall. ص. 255. ISBN:0-13-241326-4. مؤرشف من الأصل في 2019-12-12.
{{استشهاد بكتاب}}:|archive-date=/|archive-url=timestamp mismatch (مساعدة) - ^ "Joseph Henry". Member Directory, National Academy of Sciences. مؤرشف من الأصل في 2018-07-20. اطلع عليه بتاريخ 2016-12-30.
- ^ Faraday، Michael؛ Day، P. (1 فبراير 1999). The philosopher's tree: a selection of Michael Faraday's writings. CRC Press. ص. 71. ISBN:978-0-7503-0570-9. مؤرشف من الأصل في 2020-01-07. اطلع عليه بتاريخ 2011-08-28.
- ^ Michael Faraday, by L. Pearce Williams, pp. 182–3
- ^ Michael Faraday, by L. Pearce Williams, p. 191–5
- ^ أ ب Michael Faraday, by L. Pearce Williams, p. 510
- ^ Maxwell, James Clerk (1904), A Treatise on Electricity and Magnetism, Vol. II, Third Edition. Oxford University Press, pp. 178–9 and 189.
- ^ "Archives Biographies: Michael Faraday", The Institution of Engineering and Technology. نسخة محفوظة 15 يونيو 2018 على موقع واي باك مشين.
- ^ Lenz, E. (1834), "Ueber die Bestimmung der Richtung der durch elektodynamische Vertheilung erregten galvanischen Ströme", Annalen der Physik und Chemie, 107 (31), pp. 483–494. A partial translation of the paper is available in Magie, W. M. (1963), A Source Book in Physics, Harvard: Cambridge MA, pp. 511–513. نسخة محفوظة 14 يونيو 2018 على موقع واي باك مشين.
- ^ Poyser, Arthur William (1892), Magnetism and electricity: A manual for students in advanced classes. London and New York; Longmans, Green, & Co., p. 285, fig. 248. Retrieved 2009-08-06. نسخة محفوظة 02 فبراير 2017 على موقع واي باك مشين.
- ^ "Faraday's Law, which states that the electromotive force around a closed path is equal to the negative of the time rate of change of magnetic flux enclosed by the path"Jordan، Edward؛ Balmain، Keith G. (1968). Electromagnetic Waves and Radiating Systems (ط. 2nd). Prentice-Hall. ص. 100.
{{استشهاد بكتاب}}: صيانة الاستشهاد: التاريخ والسنة (link) - ^ "The magnetic flux is that flux which passes through any and every surface whose perimeter is the closed path"Hayt، William (1989). Engineering Electromagnetics (ط. 5th). McGraw-Hill. ص. 312. ISBN:0-07-027406-1. مؤرشف من الأصل في 2019-12-17.
- ^ Neumann، Franz Ernst (1846). "Allgemeine Gesetze Der Inducirten Elektrischen Ströme" (PDF). Annalen der Physik. ج. 143 ع. 1: 31–44. Bibcode:1846AnP...143...31N. DOI:10.1002/andp.18461430103. مؤرشف من الأصل (PDF) في 12 مارس 2020. اطلع عليه بتاريخ أغسطس 2020.
{{استشهاد بدورية محكمة}}: تحقق من التاريخ في:|تاريخ الوصول=(مساعدة) - ^ Yehuda Salu (2014). "A Left Hand Rule for Faraday's Law". مدرس الفيزياء (مجلة). ج. 52: 48. Bibcode:2014PhTea..52...48S. DOI:10.1119/1.4849156.
- ^ Salu، Yehuda. "A Left Hand Rule for Faraday's Law". www.PhysicsForArchitects.com/bypassing-lenzs-rule. مؤرشف من الأصل في 2018-06-30. اطلع عليه بتاريخ 2017-07-30.
- ^ Harrington، Roger F. (2003). Introduction to electromagnetic engineering. Mineola, NY: Dover Publications. ص. 56. ISBN:0-486-43241-6. مؤرشف من الأصل في 2016-12-02.
- ^ "The flux rule" is the terminology that Feynman uses to refer to the law relating magnetic flux to EMF. Feynman، R. P. (2006). Leighton، R. B.؛ Sands، M. L. (المحررون). The Feynman Lectures on Physics. San Francisco: Pearson/Addison-Wesley. Vol. II, p. 17-2. ISBN:0-8053-9049-9. مؤرشف من الأصل في 5 مايو 2020. اطلع عليه بتاريخ أغسطس 2020.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ الوصول=(مساعدة) - ^ Griffiths، David J. (1999). Introduction to Electrodynamics (ط. Third). Upper Saddle River NJ: Prentice Hall. ص. 301–303. ISBN:0-13-805326-X. مؤرشف من الأصل في 2020-01-02.
- ^ Davison، M. E. (1973). "A Simple Proof that the Lorentz Force, Law Implied Faraday's Law of Induction, when B is Time Independent". American Journal of Physics. ج. 41 ع. 5: 713. Bibcode:1973AmJPh..41..713D. DOI:10.1119/1.1987339.
- ^ Krey؛ Owen. Basic Theoretical Physics: A Concise Overview. ص. 155. مؤرشف من الأصل في 2019-12-17.
- ^ Poyser, Arthur William (1892), Magnetism and electricity: A manual for students in advanced classes. London and New York; Longmans, Green, & Co., p. 285, fig. 248. Retrieved 2009-08-06. نسخة محفوظة 02 فبراير 2017 على موقع واي باك مشين.
- ^ "Joseph Henry". Distinguished Members Gallery, National Academy of Sciences. مؤرشف من الأصل في 2012-11-28. اطلع عليه بتاريخ 2006-11-30.
- ^ Alexander، Charles؛ Sadiku، Matthew (2009). Fundamentals of Electric Circuits (ط. 3). McGraw-Hill. ص. 211.
- ^ Also called electric generator, electrical generator, and electromagnetic generator.
- ^ Tom McInally, The Sixth Scottish University. The Scots Colleges Abroad: 1575 to 1799 (Brill, Leiden, 2012) p. 115
- ^ OLEG D. JEFIMENKO, Electrostatic Motors, Their History, Types, and Principles of Operation, Electret Scientific Company - 1973, page 22-45
وصلات خارجية[عدل]
- محاكاة باللغة الجافا لحقل كهرومغناطيسي حركي (بالإنجليزية)
| في كومنز صور وملفات عن: قانون فاراداي |









