مؤشر أويلر

  لمعانٍ أخرى، طالع مؤشر (توضيح).

القيم الألف الأولى ل (φ(n

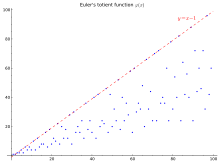
في نظرية الأعداد، مؤشر أويلر (بالإنجليزية: Euler's totient function)‏ هو دالة معرفة على مجموعة الأعداد الطبيعية. تستعمل في الرياضيات الخالصة وفي نظرية المجموعات وفي نظرية الأعداد الجبرية وفي نظرية الأعداد التحليلية. في الرياضيات التطبيقية، مروراً بالحسابيات التوافقية، تلعب دوراً مهماً في نظرية المعلومات وخاصة في التشفير. وتسمى دالة فاي لأويلر أو ببساطة دالة فاي، لأن الحرف φ مستعمل للإشارة لهذه الدالة.

وتحمل اسم الرياضي السوسري أويلر (1707 - 1783) الذي كان أول من درسها.

• مؤشر أويلر φ هي دالة من مجموعة الأعداد الطبيعية نحو نفس المجموعة، حيث صورة n بالدالة هو عدد الأعداد الأصغر من n والأولية مع n.

مثلا، φ(8) = 4 لأن الأعداد 1, 3, 5 و7 أولية مع 8.

دالة أويلر هي دالة جدائية أو ضربية أي أنه إذا كان m و n أوليين فيما بينهما، إذا: $\varphi (mn)=\varphi (m)\cdot \varphi (n)$

التاريخ والتسمية والرمز المستعل

أبدع ليونهارت أويلر هذه الدالة عام 1763م و مع ذلك في ذلك الوقت لم يقم أويلر بإختيار أي رمز للدلالة عليها. في منشور عام 1784، درس أويلر هذه الدالة بشكل أكبر، واختار الحرف اليوناني $\pi$ للدلالة عليها: كتب $\pi D$ لـ «عدد الأعداد الأقل من D ، والتي ليس لها قاسم مشترك معها».

يختلف هذا التعريف عن التعريف الحالي للدالة الكلية عند D = 1 ولكنه بخلاف ذلك هو نفسه. التدوين القياسي الحالي (φ(A يأتي من أطروحة غاوس استفسارات حسابية والتي نشرت عام 1801. على الرغم من أن غاوس لم يستخدم الأقواس حول المتغير وكتب φA. بالتالي، غالبًا ما تسمى دالة فاي لأويلر أو ببساطة دالة فاي.

حساب دالة أويلر

$\varphi (n)=n\prod _{p\mid n}\left(1-{\frac {1}{p}}\right),$

حيث يمتد هذا الجداء على القواسم الأولية المختلفة الواحد منهم عن الآخر.

مثال

$\varphi (36)=\varphi \left(2^{2}3^{2}\right)=36\left(1-{\frac {1}{2}}\right)\left(1-{\frac {1}{3}}\right)=36\cdot {\frac {1}{2}}\cdot {\frac {2}{3}}=12.$

قيمة دالة أويلر للعدد أولي

$\varphi (p)=p-1$ حيث p عدد أولي، ودالة أويلر تأخذ هذه القيمة لكل الأعداد الأولية، والسبب يرجع لأن كل الأعداد الأصغر قطعا من p هي اولية مع p.

مثال

$\varphi (19)=19-1=18$، لأن 19 عدد أولي.

قيمة دالة أويلر للقوة عدد أولي (أس)

$\varphi (p^{n})=p^{n}-p^{n-1}$، حيث p عدد أولي و n عدد صحيح موجب.

مثال

$\varphi (7^{3})=7^{3}-7^{3-1}=343-49=294$.

برهان لصيغة جداء أويلر

تنص المبرهنة الأساسية في الحسابيات على أنه إذا كان n > 1 فإنه يمكن التعبير على n عبر جداء من الأعداد الأولية $n=p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}}$، بما أن مؤشر أويلر هي دالة جدائية، لدينا

${\begin{array}{rcl}\varphi (n)&=&\varphi (p_{1}^{k_{1}})\,\varphi (p_{2}^{k_{2}})\cdots \varphi (p_{r}^{k_{r}})\\[.1em]&=&p_{1}^{k_{1}-1}(p_{1}-1)\,p_{2}^{k_{2}-1}(p_{2}-1)\cdots p_{r}^{k_{r}-1}(p_{r}-1)\\[.1em]&=&p_{1}^{k_{1}}\left(1-{\frac {1}{p_{1}}}\right)p_{2}^{k_{2}}\left(1-{\frac {1}{p_{2}}}\right)\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{r}}}\right)\\[.1em]&=&p_{1}^{k_{1}}p_{2}^{k_{2}}\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right)\\[.1em]&=&n\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right).\end{array}}$

بعض من قيم الدالة

بيان لمائة قيمة الأولى لدالة مؤشر أويلر

φ(n) for 1 ≤ n ≤ 143

+	0	1	2	3	4	5	6	7	8	9	10	11
0	غ/م	1	1	2	2	4	2	6	4	6	4	10
12	4	12	6	8	8	16	6	18	8	12	10	22
24	8	20	12	18	12	28	8	30	16	20	16	24
36	12	36	18	24	16	40	12	42	20	24	22	46
48	16	42	20	32	24	52	18	40	24	36	28	58
60	16	60	30	36	32	48	20	66	32	44	24	70
72	24	72	36	40	36	60	24	78	32	54	40	82
84	24	64	42	56	40	88	24	72	44	60	46	72
96	32	96	42	60	40	100	32	102	48	48	52	106
108	36	108	40	72	48	112	36	88	56	72	58	96
120	32	110	60	80	60	100	36	126	64	84	48	130
132	40	108	66	72	64	136	44	138	48	92	70	120

على سبيل المثال، العدد الذي يقع في تقاطع العمود الذي يحمل رقم 5 مع الخط الذي يحمل العدد 132 هو 136. سبب ذلك هو ما يلي:

$\varphi (132+5)=\varphi (137)=136$. ويعود كون $\varphi (137)$ تصغر بواحد 137 إلى كون العدد 137 أوليا.

مبرهنة أويلر

المقالة الرئيسة: مبرهنة أويلر

تنص هذه المبرهنة على أنه إذا كان a و n عددين طبيعيين أوليين فيما بينهما، فإن:

$a^{\varphi (n)}\equiv 1\mod n.\,$

الحالة الخاصة من هذه المبرهنة حينما يكون n أوليا تعرف باسم مبرهنة فيرما الصغرى.

انظر إلى مبرهنة لاغرانج (نظرية الزمر)

صيغ أخرى تحتوي على مؤشر أويلر

• $a\mid b\implies \varphi (a)\mid \varphi (b)$
• $n\mid \varphi (a^{n}-1)\quad {\text{for }}a,n>1$
• $\varphi (mn)=\varphi (m)\varphi (n)\cdot {\frac {d}{\varphi (d)}}\quad$ بحيث $d=\operatorname {gcd} (m,n)$
• $\varphi (2m)={\begin{cases}2\varphi (m)&{\text{ if }}m{\text{ is even}}\\\varphi (m)&{\text{ if }}m{\text{ is odd}}\end{cases}}$
• $\varphi \left(n^{m}\right)=n^{m-1}\varphi (n)$
• $\sum _{d\mid n}{\frac {\mu ^{2}(d)}{\varphi (d)}}={\frac {n}{\varphi (n)}}$
• $\sum _{1\leq k\leq n \atop (k,n)=1}\!\!k={\tfrac {1}{2}}n\varphi (n)\quad {\text{for }}n>1$
• $\sum _{k=1}^{n}\varphi (k)={\tfrac {1}{2}}\left(1+\sum _{k=1}^{n}\mu (k)\left\lfloor {\frac {n}{k}}\right\rfloor ^{2}\right)={\frac {3}{\pi ^{2}}}n^{2}+O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)$
• $\sum _{k=1}^{n}{\frac {\varphi (k)}{k}}=\sum _{k=1}^{n}{\frac {\mu (k)}{k}}\left\lfloor {\frac {n}{k}}\right\rfloor ={\frac {6}{\pi ^{2}}}n+O\left((\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)$

خاصية مينون

في عام 1965 أثبت كيسافا مينون أن

$\sum _{\stackrel {1\leq k\leq n}{\gcd(k,n)=1}}\!\!\!\!\gcd(k-1,n)=\varphi (n)d(n),$

بحيث $d(n)$ هو عدد قواسم العدد $.n$

معضلات غير محلولة

حدسية ليهمر

المقالة الرئيسة: معضلة مؤشر ليهمر

إذا كان p عددا أوليا، فإن φ(p) = p − 1. في عام 1932، طرح ديريك هنري ليهمر السؤال التالي: هل هناك من عدد طبيعي n مؤلف (أي غير أولي)، حيث φ(n) يقسم n -1 ؟ لا يعلم حاليا أي جواب على هدا السؤال.

في عام 1933، برهن على أنه إذا كان هذا العدد موجودا، فإنه حتما، فردي وخال من المربعات، وقابل للقسمة على سبعة أعداد أولية على الأقل (أي أن ω(n) ≥ 7).

حدسية كارميكائيل

انظر إلى حدسية دالة المؤشر لكارميكائيل.

فرضية ريمان

${\frac {n}{\varphi (n)}}<e^{\gamma }\log \log n+{\frac {e^{\gamma }(4+\gamma -\log 4\pi )}{\sqrt {\log n}}}$

• دالث بسي لديدكايند

انظر أيضًا

• تعميمات مبرهنة فيرما الصغرى
• دالة المؤشر لكارميكائيل
• عدد مؤلف للغاية
• مجموع رامانجن

وصلات خارجية

• Schneider, Robert P. عدد من المتطابقات المهمة في نظرية الأعداد (باللغة الإنجليزية).
• دالة فاي لـ «أويلر»