عدد مؤلف

العدد المؤلف أو حتى العدد المركب (بالإنجليزية: Composite number)، هو عدد صحيح موجب ذو قواسم غير بديهية يمكن التعبير عنه بضرب عددين صحيحين أصغر منه. كل عدد هو مؤلف إذا كان يقبل القسمة على عدد واحد على الأقل غير الواحد ونفسه.[1][2] بذلك يكون كل عدد صحيح أكبر من الواحد إما أوليا إما مؤلفا. أما العددان 0 و 1 فلا يعتبران أوليين ولا مؤلفين.[3]
فعلى سبيل المثال:
- العدد 14 مؤلف لأنه حاصل ضرب عددين صحيحين أصغر منه وهما 2 و 7.
- العدد 21 عدد مؤلف لأنه من الممكن كتابته جداء عوامل 3 و 7 حيث كل من 7 و 3 قواسم غير بديهية للعدد 21.
على العكس العددان 2 و 3 ليسا مؤلفين لأنه لا يمكن كتابتهم إلا في صيغة و . وكذلك الرقم 11 فهو عدد غير مؤلف (أولي) لأنه لا يمكن كتابته إلا في صورة فقط وهذه العوامل هي قواسم بديهية للرقم 11.
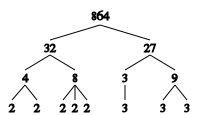
أي أن 864 = 25 × 33.
الأعداد المؤلفة الأصغر من 150 هي :
- 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 128, 129, 130, 132, 133, 134, 135, 136, 138, 140, 141, 142, 143, 144, 145, 146, 147, 148, 150. (متسلسلة A002808 في OEIS)
كل عدد مؤلف يمكن صياغته في صورة حاصل ضرب عددين أو أكثر. فعلى سبيل المثال العدد المؤلف 299 يمكن كتابته في شكل . والعدد المؤلف 360 يمكن استخدام المبرهنة الأساسية في الحسابيات لكتابته على الشكل التالي .[1]
يوجد العديد من الاختبارات لمعرفة هل اعدد أولي أم مؤلف، بدون الحاجة إلى تحليل العدد لمعرفة قواسمة المشتركة.
الأنواع
[عدل]إحدى طرق تصنيف الأعداد المؤلفة هي حساب عدد القواسم الأولية لذلك العدد. إذا كان للعدد المؤلف قاسمين أوليين فقط، يعتبر عدد نصف أولي (لا يشترط أن تكون الأعداد مختلفة، فتربيع الأعداد الأولية يتم تصنيفها أعدادا نصف أولية).
العدد المؤلف الذي له ثلاث جذور يصنف عدد sphenic. في بعض التطبيقات، يكون من الضروري التمييز بين الأعداد المؤلفة التي لها عدد فردي من القواسم الأولية المختلفة والتي لها عدد زوجي من القواسم الأولية المختلفة. مثل:

حيث
- هو دالة موبيوس.
- هو عدد له عدد زوجي من القواسم الأولية.
أما إذا كان له عدد فردي من القواسم الأولية على الشكل التالي:
يكون الناتج 1-.
إذا كانت كل الأعداد الأولية موجودة أكثر من مرة يطلق على العدد عدد قوي (Powerful number). إذا لم يتكرر أي عدد أولي يطلق على العدد عدد صحيح خال من المربعات (squarefree) (كل الأعداد الأولية بالإضافة إلى رقم 1 هي أعداد صحيحة خالية من المربعات)
على سبيل المثال:
- تم تكرار القواسم المشتركة فيسمى 72 رقم قوي (powerful).
- لم يتكرر أي من العوامل فيسمى 42 عدد صحيح خال من المربعات.
يمكن تصنيف الأعداد المؤلفة عن طريق عد عدد الأرقام التي تقبل القسمة عليه (قواسمه). كل الأعداد المؤلفة لديها على الأقل ثلاث قواسم. في حالة تربيع الأعداد الأولية، تكون هذه القواسم هي بحيث هو عدد أولي.
يمكن تسمية الأعداد المؤلفة أيضا بالأعداد المستطيلية (rectangular numbers)، ولكن هذا الاسم يمكن أن يشير إلى الأعداد البرونية (Pronic number)، وهي الأعداد الناتجة من حاصل ضرب عددين متتاليين. المجموعة التالية توضح بداية الأرقام البرونية (Pronic number):
- 0، 2 ،6، 12، 20، 30، 42، 56، 72، 90، 110، 132، 156، 182، 210، 240، 272، 306، 342، 380، 420، 462. (متسلسلة A002378 في OEIS)
انظر أيضًا
[عدل]- الدوال والثوابت الرياضية
- معادلات نيوتن-أويلر.
- الرقم الصغير.
- معادلة xʸ=yˣ.
- الأس العشري.
- عدد صحيح خال من المربعات.
- جدول التفكيك إلى عوامل أولية.
- تحليل عدد صحيح إلى عوامل.
- المبرهنة الأساسية في الحسابيات.
- غربال إراتوستينس.
- التمثيل القانوني لعدد صحيح موجب
- قضبان كويزنير
- خوارزمية شوور.
- فيزياء رياضية
- تحليل إلى عوامل
- جدول القواسم
- معدل الحرارة (الكفاءة).
المصادر
[عدل]- ^ ا ب Colilli، Paul (1981-01). "Bernardo, Aldo S. and Rigo Mignani. Ritratto Dell'Italia. 2nd Ed. Lexington, Massachusetts and Toronto: D.C. Heath and Company, 1978Bernardo, Aldo S. and Rigo Mignani. Ritratto Dell'Italia. 2nd Ed. Lexington, Massachusetts and Toronto: D.C. Heath and Company, 1978. Pp. IX, 317". Canadian Modern Language Review. ج. 37 ع. 2: 351–352. DOI:10.3138/cmlr.37.2.351. ISSN:0008-4506. مؤرشف من الأصل في 16 يونيو 2021.
{{استشهاد بدورية محكمة}}: تحقق من التاريخ في:|تاريخ=(مساعدة) - ^ J. H. P. (1970-06). "Rei Río, Amelia Agostini de. Flores del romancero. Englewood Cliffs, New Jersey, Prentice-Hall, 1970Rei Río, Amelia Agostini de. Flores del romancero. Englewood Cliffs, New Jersey, Prentice-Hall, 1970. 276 pp. $3.95 U.S." Canadian Modern Language Review. ج. 26 ع. 4: 77–77. DOI:10.3138/cmlr.26.4.77b. ISSN:0008-4506.
{{استشهاد بدورية محكمة}}: تحقق من التاريخ في:|تاريخ=(مساعدة) - ^ John B. (1976). A first course in abstract algebra (ط. 2d ed). Reading, Mass.: Addison-Wesley Pub. Co. ISBN:0-201-01984-1. OCLC:2344185.
{{استشهاد بكتاب}}:|طبعة=يحتوي على نص زائد (مساعدة)
ملاحظات
[عدل]- (Fraleigh, John B. (1976), A First Course In Abstract Algebra (2nd ed
- Herstein, I. N [الإنجليزية]-Topics In Algebra,
- Elementary Introduction to Number Theory
- Introduction To Modern Algebra, Revised Edition, Boston
- Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs













