تحليل الانحدار
| الطبيعة | |
|---|---|
| فرع من | |
| المخترع | |
| سمّي باسم | |
| جانب من |
| إحصاء |
| تحليل الانحدار |
|---|
 |
| النماذج |
| الاحتمال |
| الأصول |
تحليل الانحدار[2][3] أو تحليل الانكفاء[4][3] أو تحليل انكفائي[5][6] (بالإنجليزية: regression analysis) هو كل طريقة إحصائية يتم فيها التنبؤ بمتوسط متغير عشوائي أو عدة متغيرات عشوائية اعتمادا على قيم وقياسات متغيرات عشوائية أخرى. له عدة أنواع مثل: الانحدار الخطي، والانحدار اللوجستي، وانحدار بواسون، والتعليم المراقب والانحدار موزون الوحدة.[7][8][9]
تحليل الانحدار هو أكثر من عملية ملائمة منحنى (أي اختيار المنحنى الأكثر ملائمة لمجموعة نقاط بيانية معطاة) فهو يتضمن ملائمة نموذج باستخدام مكونات حتمية واعتباطية. المكونات الحتمية تدعى المتنبئات أما المكونات الاعتباطية فتدعى الخطأ.
الشكل الأبسط لنموذج الانحدار يحوي متغيرا تابعا (غير مستقل) (يدعى أيضا متغير الخرج، أو المتغير الداخلي أو المتغير ع) إضافة إلى متغير مستقل (يدعى العامل، أو المتغير الخارجي، أو المتغير-س).
من الأمثلة النموذجية على تحليل الانحدار: اعتماد ضغط الدم Y على عمر الشخص X، أو اعتماد الوزن لحيوانات التجربة Y على معدل التغذية اليومي X. هذا الارتباط والتابعية بين X وY هي ما ندعوه بالانحدار أو الارتباط فنقول ارتباط Y ب X.
ويلاحظ من ذلك أن نموذج الانحدار يعتمد دائماً على علاقة السببية بمعنى ان يكون التغير في المتغير المستقل مسببا رئيسيا للتغير في المتغير التابع.
ونظرية تحليل الانحدار تعتمد على النظرية الاقتصادية بين متغيرين أي أنها تفترض ثبات العوامل الأخرى.
الانحدار الخطي[عدل]
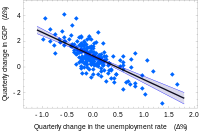
في الانحدار الخطي، تكون مواصفات هذا النموذج بشرط أن المتغير المستقل، هو توافيق خطية للوسيط. مثلاً، في الانحدار الخطي البسيط ولعمل نموذج من النقاط البيانية يوجد متغير: ، ووسيطين، و:
- الخط المستقيم:
في الانحدار الخطي المتعدد، توجد عدة متغيرات مستقلة أو دوال من المتغيرات المستقلة. مثال ذلك، إضافة عنصر في xi2 للانحدار السابق يعطي:
ما زال هذا انحداراً خطياً، بالرغم من أن التعبير على الطرف الأيمن هو دالة تربيعية في المتغير المستقل، لكنه لايزال خطياً في الوسائط , و
في كلا الحالتين، ليست حد خطأ و تدل على ملاحظة معينة. لو كان لدينا عينة عشوائية من التعداد السكاني، يمكننا تقدير وسائط السكان وإيجاد نموذج الانحدار الخطي للعينة:
الحد يمثل الراسب، . أحد طرق التقدير تتمثل في أقل التربيعات الاعتيادية، SSE:
تبسيط هذه الدالة ينجم عنه مجموعة من معادلات اعتيادية، يتم حلها لإيجاد تقديرات الوسيط، .
في حالة الانحدار الخطي البسيط، تكون صيغ تقديرات أقل التربيعات:
حيث المتوسط الحسابي (لقيم و متوسط قيم .
على افتراض أن حد الخطأ السكاني ذو تباين ثابت، تعطى تقديرات التباين بالعلاقة:
ويطلق عليها خطأ مربع المتوسط (MSE) للانحدار. تعطى الأخطاء المعيارية لتقديرات الوسيط بالعلاقة:
انظر أيضا[عدل]
مراجع[عدل]
- ^ Maria Blettner (5 نوفمبر 2010). "Linear regression analysis: part 14 of a series on evaluation of scientific publications". Deutsches Ärzteblatt international ع. 44: 776–782. DOI:10.3238/ARZTEBL.2010.0776.
- ^ المعجم الموحد لمصطلحات المعلوماتية: (إنجليزي - فرنسي - عربي). سلسلة المعاجم الموحدة (27) (بالعربية والإنجليزية والفرنسية). الرباط: مكتب تنسيق التعريب. 2000. ص. 130. ISBN:978-9981-1888-9-1. OCLC:1227668516. QID:Q113996988.
- ^ أ ب أفرام بوروفسكي؛ جوناتان بوروين (1995)، معجم الرياضيات: إنكليزي - فرنسي - عربي، المعاجم الأكاديمية المتخصصة (بالعربية والإنجليزية والفرنسية)، ترجمة: علي مصطفى بن الأشهر، مراجعة: محمد الدبس، بيروت: أكاديميا إنترناشيونال، ج. 3، ص. 525، OCLC:822262215، QID:Q121833036
- ^ موفق دعبول؛ بشير قابيل؛ مروان البواب؛ خضر الأحمد (2018)، معجم مصطلحات الرياضيات (بالعربية والإنجليزية)، دمشق: مجمع اللغة العربية بدمشق، ص. 590، OCLC:1369254291، QID:Q108593221
- ^ معجم المصطلحات المعلوماتية (بالعربية والإنجليزية)، دمشق: الجمعية العلمية السورية للمعلوماتية، 2000، ص. 450، OCLC:47938198، QID:Q108408025
- ^ نزار الحافظ (2007)، مسرد مصطلحات المعلوماتية (بالعربية والإنجليزية)، الجمعية العلمية السورية للمعلوماتية، ص. 67، QID:Q108442159
- ^ Necessary Condition Analysis نسخة محفوظة 31 أغسطس 2017 على موقع واي باك مشين.
- ^ Tofallis، C. (2009). "Least Squares Percentage Regression". Journal of Modern Applied Statistical Methods. ج. 7: 526–534. DOI:10.2139/ssrn.1406472. SSRN:1406472.
- ^ Armstrong، J. Scott (2012). "Illusions in Regression Analysis". International Journal of Forecasting (forthcoming). ج. 28 ع. 3: 689. DOI:10.1016/j.ijforecast.2012.02.001. مؤرشف من الأصل في 2012-09-23.
وصلات خارجية[عدل]
| في كومنز صور وملفات عن: تحليل الانحدار |
























