غاز مثالي
| صنف فرعي من | |
|---|---|
| الاستعمال | |
| يدرسه | |
| تعريف الصيغة | |
| النقيض |
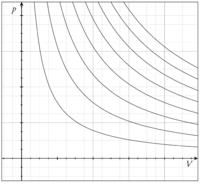
الغاز المثالي[1] (بالإنجليزية: ideal Gas) هو نموذج فيزيائي ثرموديناميك لتصرف المادة في الحالة الغازية. يفرض النموذج عدم وجود تفاعل بين جزيئات الغاز وأن جزيئات الغاز نقطية، لذا فإنه مناسب لوصف غازات ذات كثافة منخفضة، كما ينطبق على الغازات الخاملة مثل الهيليوم والنيون والآرغون التي لا تكوّن جزيئات وتكون ذراتها منفردة. هذ النموذج اكتشف في القرن 19.
مواصفات الغاز المثالي[عدل]
هذا النموذج يخضع خضوعا مطلقا لقانون بويل-ماريوط. ويخضع أيضا لقانون أفوجادرو
للغاز المثالي شروط وهي على النحو التالي:
- حجم جزيئات الغاز مهملة بالنسبة للوعاء الذي يحتويه أي تحت ضغط منخفض.
- التصادمات بين جزيئات الغاز تصادمات مرنة.
- حركة جزيئات الغاز حركة عشوائية دون مؤثرات خارجية.
فالغاز المثالي هو غاز افتراضي لتسهيل التعامل مع الكثير من المتغيرات في المواضيع التي تتناولها الديناميكا الحرارية. والفرضيات أو الشروط الثلاثة هي التي تجعل الغاز الحقيقي إذا وجد في هذه الظروف يتصرف كغاز مثالي.
حجم جزيئات الغاز مهملة بالنسبة للوعاء الذي يحتويه أي تحت ضغط منخفض:
لا يمكن أن يوجد غاز ندرسه إلا وجد في وعاء وإذا قمنا بحساب حجم جزيئات الغاز وقارناها بحجم الوعاء نجده مهملا وهذا يتحقق عندما يكون ضغط الغاز عند الضغط الجوي أو أقل وعند درجة حرارة الغرفة. أما إذا وجد في ظروف من الضغط العالي مثل غاز في جرة (كغاز الفرن المستخدم للطهي) فهو لن يتصرف كغاز مثالي ولا يمكن أن نهمل حجم الغاز بالنسبة للجرة.
التصادمات بين جزيئات الغاز تصادمات مرنة: (collision involving gas molecules are totally elastic)
هذا يفترض ان الجزئيات لا تفقد أي من طاقتها عندما تتصادم مع بعضها البعض.
حركة جزيئات الغاز حركة عشوائية دون مؤثرات خارجية:
الحركة العشوائية هي تلك الحركة التي لا تخضع لأي قانون فيزيائي يمكن أن يتنبأ بها وهذه الجزئيات تتحرك بهذه الطريقة ولا يمكن أن نعرف مسار أي جزئ وكيف سيكون، لذلك نفترض ان حركة الجزئيات حركة عشوائية.
طبعا هذه الفرضيات تتحقق في ظروف محددة وذلك للاقتراب قدر الإمكان لوضع قانون يحكم متغيرات الغاز (الضغط والحجم ودرجة الحرارة).
معادلة الغاز المثالي[عدل]
أو معادلة الحالة الحرارية لغاز مثالي وهي تصف غازا مثاليا وسلوكه عند تغير درجة الحرارة مثلاً. وقد شكلت تلك المعادلة كنتيجة لنتائج تجارب عديدة (قوانين الغازات). ثم استطاع لودفيغ بولتزمان عن طريق حساب الاحتمالات (ترموديناميكا إحصائية) تفسير سلوك الغاز على أساس بنية جسيمات الغاز.
تصف معادلة الغاز العامة دوال حالة غاز مثالي وعلاقات تلك الدوال بعضها ببعض من: درجة الحرارة، والضغط وحجم الغاز. وهي تكتب في الكيمياء والفيزياء بصيغ مختلفة ولكنها كلها لها مدلول واحد.
حيث:
ثابت الغازات العام، كما أن:
- تسمى «ثابت الغاز النوعي».
بواسطة المعادلة العامة للغازات بالإضافة إلى قوانين الديناميكا الحرارية يمكننا وصف عمليات الحركة الحرارية للغازات المثالية بطريقة الرياضيات.
- هي ثابت بولتزمان وعلاقته بثابت الغازات العام كالآتي:
- N = R.
- حيث N ثابت أفوجادرو الذي يعطي عدد الجزيئات في 1 مول من المادة.
على وجه العموم، يكفي معرفة واحدة من المعادلات أعلاه في كونها المعادلة العامة للغازات، مثل:
وفيها :
- p الضغط
- V الحجم المولي
- T درجة الحرارة بالكلفن
- R ثابت الغازات العام
- n عدد المولات (أو أجزاء المول).
اقرأ أيضاً[عدل]
مراجع[عدل]
- ^ معجم مصطلحات الكيمياء (بالعربية والإنجليزية والفرنسية) (ط. 1)، دمشق: مجمع اللغة العربية بدمشق، 2014، ص. 254، OCLC:931065783، QID:Q113378673
- ^ "CODATA Recommended Values: molar gas constant". National Institute of Standards and Technology. اطلع عليه بتاريخ 2012-01-12.
| غاز مثالي في المشاريع الشقيقة: | |







