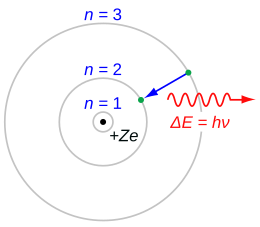
نموذج بور

نموذج بور للذرة

في الفيزياء الذرية نموذج بور يصور الذرة كنواة صغيرة موجبة الشحنة محاطة بالإلكترونات الموجودة في مدارات - وذلك مثل النظام الشمسي. ونظرا لسهولة هذا النموذج فإنه لا يزال يستخدم كمقدمة لدارسي ميكانيكا الكم.سمي هذا النموذج "نموذج بور " على اسم العالم الفيزيائي الكبير بور الذي اقترحه لتمثيل ذرة الهيدروجين بحيث يتطابق هذا النموذج مع خطوط الطيف المنبعثة من ذرات الهيدروجين ويفسرها .

في أوائل القرن العشرين، أثبتت التجارب التي أجراها إرنست راذرفورد وأخرون أن الذرة تتكون من الكترون سالبة الشحنة تدور في مدارات حول نواة كثيفة وصغيرة وموجبة الشحنة.

وأبسط أنواع الذرات هي ذرة الهيدروجين، والتي تتكون من بروتون وإلكترون مرتبطان معا القوى الكهرستاتيكية. وهذا مخالف لنظام الأرض-الشمس، والذي يتم الارتباط فيه عن طريق قوى الجاذبية.

في نموذج بور يمكن للإلكترونات أن تكون فقط على مسافة محددة من البروتون المرتبطة به. وعند تواجدها في أى مكان أخر فإنه يستلزم فقد طاقة (بالإشعاع الضوئي) وأخيرا يقل نصف قطر دوران الإلكترون حول البروتون حتى تسقط فيه مما يؤدى لتدمير الذرة. وقد كان هناك دعم لهذه النظرية بخطوط الطيف، والتي وضحت أن الإلكترونات التي تدور في مدارات ينبعث منها ضوء في ترددات وطاقات معينة.

وعلى هذا فقد إقترح بور في عام 1913 الآتى :

1. تدور الإلكترونات في مدارات دائرية لها طاقات كمية منفصلة حول البروتون تحت تأثير قوة التجاذب لكولوم.
2. قوانين الميكانيكا التقليدية لا يمكن تطبيقها عندما يقوم الإلكترون بعمل القفزات بين المدارات المسموح له التواجد فيها، تطبق فقط عند المدارات الثابتة للإلكترون حيث لا يبعث طاقة.
3. عندما يقوم إلكترون بعمل قفزة من مدار لأخر فإن فرق الطاقة إما يكتسب أو يفقد بوحدة واحدة كمية من الطاقة (تسمى فوتون)، والذي له طاقة تساوى الفرق بين طاقتى المدارين.
4. المدارات المسموحة تعتمد على قيم الكمات المنفصلة للمدار العزم الزاوي L طبقا للمعادلة

$\mathbf{L} = n \cdot \hbar = n \cdot {h \over 2\pi}$

حيث n=1,2,3,...etc وتسمى عدد العزم الزاوي الكمي

الافتراض رقم (4) ينص على أن أقل مستوى n=1. ينطبق على أقل نصف قطر 0.0529 نانو متر، والذي يعرف بنصف قطر بور. وعندما يتواجد إلكترون في أقل مدار، لا يمكن أن يقترب من البروتون لأقل من هذه القيمة.

ولوصف أكثر دقة للذرة راجع ميكانيكا الكم. المعالجة الكاملة من ناحية ميكانيكا الكم للذرة أكثر دقة - ولكنها حسابيا أكثر تعقيدا، واستخدام نموذج بور يمكن أن يعطى نتائج مفيدة بمجهودات أقل. والشيء الذي يجب تذكره ومثل النماذج الأخرى، فإن هذا النموذج يساعد في فهم تركيب الذرة، والتي ليست مجرد نظام شمسي مصغر.

استنتاج مستويات الطاقة الإلكترونية للهيدروجين

نموذج بور دقيق فقط لنظام يحتوى على إلكترون واحد فقط مثل ذرة الهيدروجين أو الأيون الأحادى للهيليوم. وسيتم استخدام نموذج بور لاستنتاج مستويات الطاقة للهيدروجين.

وسنقوم بالبدء ببيان ثلاثة فروض أولية :

• 1- كل الجسيمات لها طبيعة موجية (انظر ازدواجية موجة-جسيم)، والطول الموجي للإلكترون $\lambda$، يتناسب مع سرعته v كالتالي :

$\lambda = \frac{h}{m_e v}$

حيث، h هي ثابت بلانك، $m_e$ هي كتلة الإلكترون. ولم يقم بور بعمل هذا الافتراض (والذى يعرف بطول موجة دي برولي) في شكله المشتق الأصلي، لأنه لم يكن قد تم فرضه في هذا الوقت. عموما فإن هذا يسمح بلإفتراض الآتي :

• 2- محيط المدار الذي يدور فيه الإلكترون لابد أن يكون ناتج من ضرب رقم صحيح في قيمة الطول الموجي للإلكترون :

$2 \pi r = n \lambda \,$

حيث، r نصف قطر المدار الذى يدور فيه الإلكترون، n هي رقم صحيح.

• 3- يظل الإلكترون في المدار عن طريق قوى كولوم، وهذه القوى تساوى قوة الجذب المركزية :

$\frac{ke^2}{r^2} = \frac{m_e v^2}{r} \,$

حيث $k = 1 / {4 \pi \epsilon _0}$, وe هي شحنة الإلكترون.

وهذه ثلاث معادلات مع ثلاث معطيات غير معلومة : $\lambda$ وr، v. وبعد حل معادلات هذا النظام نجد معادلة واحدة خاصة بالمجهول v نضعها في المعادلة الخاصة بالطاقى الإجمالية للإلكترون :

$E \,$	$=E_{kinetic} + E_{potential} \,$
	$= \begin{matrix} \frac{1}{2} \end{matrix}m_e v^2 - \frac{k e^2}{r}$

وبسبب نظرية فايريال يتم تبسيط الطاقة الكلية لتصبح :

$E = -\begin{matrix} \frac{1}{2} \end{matrix}m_e v^2$

وأخيرا نجد معادلة تعطينا الطاقة للمستويات المختلفة للهيدروجين :

$E _n \,$	$= -2 \pi^2 k^2 \left(\frac{m_e e^4}{h^2} \right) \frac{1}{n^2} \,$
	$= \frac{-m_e e^4}{8 h^2 \epsilon_{0}^2} \frac{1}{n^2} \,$
	$= \frac{-13.6 \ \mathbf{eV}}{n^2} \,$

وعلى هذا، يكون أقل مستويات الطاقة للهيدروجين n=1 يساوى -13.6 eV. ومستوى الطاقة التالى 'n=2 يساوى -3.4 eV، والثالث 'n=3 يساوى -1.51 eV، وهكذا.

لاحظ أن كل هذه الطاقات أقل من الصفر، وهذا يعنى أن الإلكترون في حالة ارتباط مع البروتون.

الانتقال بين مستويات الطاقة (معادلة رايدبيرج)

عندما ينتقل الإلكترون من مستوى طاقة لمستوى آخر ، فإنه يطلق فوتونا (شعاع ضوء ذو طول موجة محددة (كمومية) . وباستخدام المعادلة الخاصة بمستويات الطاقة للهيدروجين يمكن تحديد الأطول الموجية للضوء الذي يمكن أن ينبعث من الهيدروجين.

أولا يتم حساب الطاقة التي تنبعث من الهيدروجين بحساب الفرق بين مستويين من مستويات طاقة الهيدروجين :

$E=E_i-E_f=\frac{m_e e^4}{8 h^2 \epsilon_{0}^2} \left(\frac{1}{n_{f}^2} - \frac{1}{n_{i}^2} \right) \,$

حيث $n_f$ تعنى مستوى الطاقة الأخير، و$n_i$ تعنى مستوى الطاقة المبدئي (بافتراض ان مستوى الطاقة الأخير أقل من المستوى المبدئي).

وحيث ان طاقة الفوتون تساوي :

$E=\frac{hc}{\lambda} \,$

يكون الطول الموجي للفوتون المنبعث يساوي :

$\frac{1}{\lambda}=\frac{m_e e^4}{8 c h^3 \epsilon_{0}^2} \left(\frac{1}{n_{f}^2} - \frac{1}{n_{i}^2} \right) \,$

والذى يعرف بمعادلة رايدبيرج.

وهذه المعادلة كانت معروفة للعلماء الذين قاموا بعمل دراسة للطيف في القرن التاسع عشر، ولكن لم يكن لديهم إثبات نظري للمعادلة حتى قام بور بفرض نظريته.

القصور في نموذج بور

فشل نموذج بور في تفسير الآتى :

1. تفسير أطياف العناصر الأثقل من الهيدروجين، فهي بالكاد تفسر الذرات التي لها إلكترون وحيد.
2. الفروق النسبية لخطوط الطيف.
3. تواجد خطوط طيف البنية الدقيقة.
4. تأثير زيمان - والتي تفسر وجود تغير في خطوط الطيف عند وجود مجال مغناطيسي خارجى.

شاهد أيضا

• ذرة
• تجربة فرانك-هرتز
• ذرة الهيدروجين
• نيلز بور
• سلسلة ليمان
• ميكانيكا الكم
• معادلة رايدبيرج
• معادلة شرودنجر
• مبدأ أوفباو

المصادر

• بور، نيلز (1913). تركيب الذرات والجزيئات (الجزء 1 من 3)
• بور، نيلز (1913). تركيب الذرات والجزيئات (الجزء 2) الأنظمة التي تحتوى على نواة وحيدة الإلكترون. Philosophical Magazine 26: 476-502
• بور، نيلز (1913). تركيب الذرات والجزيئات (الجزء 3) Philosophical Magazine 26: 857-875.
• بور، نيلز (1914). طيف الهيليوم والهيدروجين. Nature 92: 231-232.
• Tipler, Paul; Llewellyn, Ralph 2002، الفيزياء الحديثة (الطبعة الرابعة) W. H. Freeman رقم ID=ISBN 0-7167-4345-0