ثابت بلانك
| وحدات | قيم ثابت بلانك h [1] |
|---|---|
| جول·ثا | 6.626070040(81)×10−34 |
| إلكترون فولت·ثا | 4.135667662(25)×10−15 |
| وحدات | قيم ثابت بلانك المخفض ħ (h-بار) = h/2π |
| ج·ثا | 1.054571800(13)×10−34 |
| إف·ثا | 6.582119514(40)×10−16 |
ثابت بلانك هو ثابت فيزيائي له الرمز وهو يستخدم لوصف الكوانتا «أصغر مقدار للطاقة» فهو بذلك يلعب الدور الرئيسي في ميكانيك الكم. يعود اكتشافه إلى العالم الألماني ماكس بلانك عام 1900 م. يقابل هذا الثابت قيمة أخرى هي قيمة هذا الثابت مقسومة على ورمزه ويلفظ «آش بار» وفي تلك الحالة يسمى «ثابت بلانك المخفض» الذي يسمى أحيانا ثابت ديراك نسبة للعالم بول ديراك.
وحدات وقيم[عدل]
ثابت بلانك هو عبارة عن أصغر وحدة للطاقة (الجول) مضروبة بوحدة الزمن (ثانية) وبالتالي يمثل ثابت بلانك وحدة شغل أو وحدة قدرة (جول.ثانية). وهو يمثل أصغر وحدة للشغل في الكون، أي لا يوجد ما هو أقل منها، وهي تلعب دورًا أساسيًا في السلوك الفيزيائي للمادة والطاقة، وتعتبر من لبنات خلق الكون، مثل الجاذبية والشحنة الأساسية وسرعة الضوء وغيرها.
قيمة ثابت بلانك هي:
وباستخدام إلكترون فولت كوحدة لقياس الطاقة يكون لدينا:
ثابت بلانك المخفض[عدل]
نستعمل في الفيزياء ثابت بلانك المخفض وهو ثابت بلانك مقسوما على . يستخدم ثابت بلانك المخفّض في المجالات المختلفة للفيزياء، والتعبير عنه بالرمز يساعد على اختصار المعادلات:
وبناء على ذلك فقيمة تساوي بوحدات [جول. ثانية] أو إلكترون فولت.ثانية هي:
وباستخدام الإلكترون-فولت كوحدة للطاقة:
حيث:
خطأ رياضيات (خطأ في الصياغة): {\displaystyle \pi≈3.141592654 }
ولادة ثابت بلانك[عدل]
تم طرح ثابت بلانك في البداية من قبل العالم ماكس بلانك لتفسير سلوك إشعاع الجسم الأسود، حيث أن الفرضية الأساسية لقانون بلانك تعتبر أن إصدار الإشعاع الكهرومغناطيسي بواسطة الجسم الأسود يمكن تمثيله بشكل هزاز توافقي يتحرك بطاقة كمومية على الشكل التالي:
حيث: هي الطاقة الكمومية للفوتونات التي تملك تواتر (هرتز) أو تردد زاوي (راديان/ثانية).
طبقا للنظرية الكمومية تتغير طاقة الهزاز التوافقي بطاقات «منفصلة» كالآتي:
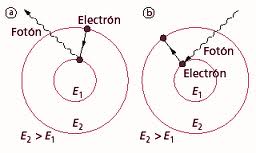
وهكذا. أي أن الإلكترون في الذرة باعتباره هزازًا توافقيًا لا يمكنه إلا الانتقال بين مستويات للطاقة منفصلة، وهذا ما يعني كمومية أو «كم». أي ينتقل إلكترون من مستوى طاقة (في الذرة) سفلي إلى مستوى طاقة أعلى عن طريق امتصاص «كم» معين من الطاقة، وعندما يقفز من مستوى طاقة عالي إلى مستوى منخفض فهو يصدر «كمًا» يعادل فارق الطاقتين في هيئة فوتون أي شعاع ضوء.
الاستخدام[عدل]
يستخدم ثابت بلانك في وصف كمومية الطاقة في النطاق الصغري، نطاق الذرات والجزيئات وما هو دونها من جسيمات أولية كالإلكترون والبروتون. في هذا العالم الصغري يختلف سلوك الطبيعة اختلافًا جذريًا عن سلوكها في النطاق الكبير من المنظور إلى الكواكب والنجوم والمجرات. في الأنطمة الكبيرة تتحكم فيها الجاذبية وتتحكم في سلوكها قوى كهرومغناطيسية (كهربائية ومغناطيسية)، أما في النطاق الصغري ففيها تسود الكمومية وتتغير الطاقة بقفزات ولا تتغير بطريقة مستمرة. فعلى سبيل المثال: إذا كان لدينا فوتون من الضوء ذو طاقة وتواتر فإن العلاقة بين تواتر الفوتون وطاقته تعتمد على ثابت بلانك طبقًا للمعادلة:
حيث n عدد حقيقي كامل مساويًا 1، 2، 3، وهكذا.
معنى ذلك أن طاقة الفوتون لا تستطيع إلا أن تتخذ القيم أو أو وهكذا. وبالتالي لا يمكن للفوتون اتخاذ القيمة مثلًا أو للطاقة، فطاقته تقفز بين مستويات للطاقة منفصلة discret values، وهذا ما نراه بالتجارب العملية في دراسة طيف الهيدروجين وأطياف العناصر أخرى. نجد أن طاقة الفوتونات تتبع هذا النمط العجيب «الكمي» أو «الكمومي»، وهكذا اكتشف الإنسان الظاهرة الكمومية، والتي تنطبق على الذرات والجزيئات والجسيمات الأولية تحت الذرية.
تلك النتيجة أوضحتها حلول معادلة شرودنجر التي تصف سلوك الإلكترون في الذرة. وأحيانًا تصف طاقة الإلكترون ليس بالتواتر وإنما بالتردد الزاوي. وبناء عليه يمكن صياغة طاقة الفوتونات التي يطلقها إلكترون الذرة باستخدام التردد الزاوي على الصورة:
- حيث
وهذه هي ظاهرة كمومية الطاقة التي أزالت مفهوم الطاقة المستمرة.
مبدأ عدم التأكد[عدل]
ثابت بلانك يظهر أيضاً في مبدأ عدم التأكد الذي اكتشفه العالم الألماني فرنر هايزنبرج، والذي ينص على أنه «لا يمكننا أن نحدد بدقة وآنيا معاً موضع وسرعة جسيم، فإذا استطعنا تحديد سرعة الجسيم بدقة تعذر علينا تعيين موضعه بدقة والعكس صحيح». والصياغة الرياضية لهذا المبدأ هي:
حيث:
- الخطأ في قياس الموضع ،
- الخطأ في قياس زخم الحركة .
والمعادلة تقول أن حاصل ضرب الخطأ في تعيين موضع الجسيم في الخطأ في تعيين زخم حركته لا بد وأن يكون أكبر من المقدار . وعلى ذلك لا يمكن أن يكون حاصل ضرب الخطأ للموقع في الخطأ في تعيين زخم حركة الجسيم لا يمكن أن تكون صفرا. وهذا ما أدهشه وأدهش العلماء آنذاك واحتج الكثيرون على تلك النتيجة واعتبر بعضهم أن حسابات هايزنبرج هراء، واشتدت المناقشات وأجريت تجارب واقعية وتجارب تخيلية لتفنيد هذا المبدأ، ولكن ثبتت صحة المبدأ عمليًا وفكريًا، وأصبح هذا المبدأ من مفاهيمنا الحديثة للطبيعة، وعمل على تعميق جذري لفهمنا للطبيعة حولنا وفي الكون بصفة عامة.
ويمكننا أيضا صياغته بالشكل:
حيث:
- الارتياب في كمية الحركة.
- الارتياب في الموقع.
- ثابت بلانك.
من النتائج الباهرة لهذا المبدأ ما قاله هايزنبرج في تفسيره: «أننا لا يمكننا معرفة المستقبل ليس بسبب عدم معرفتنا بالحاضر، وإنما بسب عدم استطاعتنا معرفة الحاضر».
أهمية ثابت بلانك[عدل]
يعتبر ثابت بلانك إلى جانب سرعة الضوء في الفراغ وثابت الجاذبية من أهم الثوابت الطبيعية على الإطلاق لأنهم يحددون إلى جانب قوى أساسية وكتلة الإلكترون وكتلة البروتون وشحنة أولية تكوين الكون كله من نجوم ومجرات ومن كواكب ومن أرض نشأت عليها الحياة.
ثابت ديراك: هو ثابت بلانك مقسومًا على ورمزه ويلفظ «آش بار»، وهذا الاختصار الذي يسهل العمليات الحسابية. يسمى كثيرًا «ثابت بلانك المخفض».
اقرأ أيضا[عدل]
المراجع[عدل]
- ^ Barry N. Taylor, Peter J. Mohr, "2014 CODATA recommended values," 31 December 2014. : [1] نسخة محفوظة 01 ديسمبر 2017 على موقع واي باك مشين.