قانون كولوم
| قانون كولوم | |
|---|---|
| النوع | قانون فيزيائي |
| الصيغة | |
| سميت باسم | شارل أوغستان دي كولوم |
| صاحبها | شارل أوغستان دي كولوم |
| تعديل مصدري - تعديل | |
| جزء من سلسلة مقالات حول |
| الكهرومغناطيسية |
|---|
 |
| بوابة كهرومغناطيسية |

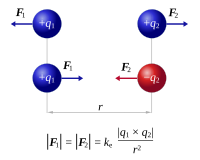
قانون كولوم، أو قانون التربيع العكسي لكولوم هو قانون تجريبي يصف التفاعل الكهرو ستاتيكي بين الجسيمات المشحونة كهربياً، وقد نشر عام 1785 من قبل الفيزيائي الفرنسي شارل أوجستين دي كولوم وكان أساساً في تطوير النظرية الكهرومغناطيسية، هو يعتبر مماثل لقانون التربيع العكسي لإسحاق نيوتن الذي يصف الجاذبية الكونية، كما يمكن استخدام قانون كولوم لاشتقاق قانون جاوس والعكس صحيح، وقد جرى اختبار القانون باستفاضة، ولقد أيدت جميع الملاحظات مبدأه.
نص قانون كولوم[عدل]
«قوة التجاذب أو التنافر بين شحنتين في الفراغ تتناسب طردياً مع القيمة المطلقة لحاصل ضرب شحنتيهما، وعكساً مع مربع المسافة بينهما».
الصيغة الرياضية[عدل]
حيث أن:
- : هي القوة المتبادلة بين الشحنتين بوحدة نيوتن.
- : قيمة الشحنة الأولى بوحدة كولوم.
- : قيمة الشحنة الثانية بوحدة كولوم.
- : متجه الوحدة وقيمته تساوي واحد واتجاهه من الشحنة الأولى إلى الشحنة الثانية.
- : مربع المسافة بين الشحنتين بوحدة متر تربيع.
ملاحظات حول القانون[عدل]
- قيمة الشحنتين تعوض بدون إشارة (يعني الشحنة السالبة تعوض في القانون بدون الإشارة السالبة).
- في نهاية الحل وبعد إيجاد قيمة القوة يجب تحديد اتجاه القوة (ما إذا كانت تجاذب أم تنافر) وسيتم توضيح ذلك في جزء لاحق.
- الوحدات السابقة كانت حسب النظام الدولي للوحدات وتختلف بالنسبة للأنظمة الأخرى.
إثبات قانون كولوم[عدل]
- القوة تتناسب طردياً مع مقدار الشحنتين.
- القوة تتناسب عكسياً مع مربع المسافة بين الشحنتين.
شكل عددى للقانون[عدل]
يمكن القول أن قانون كولوم في عددي شُكل على النحو الآتى:
تتناسب القوة الكهروستاتيكية بين اثنين من نقاط الشحنات الكهربائية تناسبا طرديا مع حاصل ضرب الشحنتين، ويتناسب عكسيا مع مربع المسافة بين الشحنتين.
حيث r هي المسافة بين مركزي الشحنتين،
- q_1 شحنة الجسيم 1 و q_2 شحنة الجسيم 2،
- وke ثابت كولوم.
ثابت كولوم[عدل]
k : هو ثابت كولوم ووحدة قياسه هي نيوتن متر مربع لكل كولوم تربيع. و هو حسب العلاقة:
ويمكن حسابه بالضبط:
بحكم تعريفها في نظام الوحدات الدولي سرعة الضوء في الفراغ المرموز لها C'O' [1] هي 299792458 متر.ثانية1 والثابت المغناطيسي (μ0)، تـُعرّف كالتالي nowrap|4π × 10−7 هـ·م،، يؤدي إلى تعريف الثابت الكهربائي (ε0) كالتالي ε0 = 1/(μ0
c2
0) ≈ 8.854187817×10−12 ف·م−1.في وحدات cgs، وحدة الشحنة، esu of charge أو ستات كولوم statcoulomb، تـُعرّف بحيث أن تلك ثابت القوة «كولوم» يكون قيمته 1.
المجال الكهربي[عدل]
بناء على قانون قوى لورنتز فإن مقدار المجال الكهربائي (E) الذي تولده شحنة نقطية واحدة (q) على مسافة معينة (r) هو:
للحصول على شحنة موجبة، وجهت الإتجاه من النقاط على طول خطوط الحقل الكهربائي بعيداً شعاعيا من موقع الشحنة النقطية، في حين أن الإتجاه هو عكس الشحنة سالبة، وحدات SI للمجال الكهربي هي فولت لكل متر أو نيوتن في الكولوم.
جهد كولوم[عدل]
يستخدم ثابت كولوم لتعيين الجهد الكولومي (الكهربائي):
- ثابت كولوم يكتب أحيانا في الصيغة:
حيث: : سماحية الفراغ الكهربية
وعلاقته بقانون كولوم كالآتي:
- .
جهد كولوم :
- .
حيث:
- q الشحنة النقطية،
- Q الشحنة المركزية
يستخدم هذا الجهد الكهربائي أحيانا كتبسيط لجهد النواة الذرية التي يدور حولها إلكترون (انظر ذرة الهيدروجين.
توزيع الشحنة المتصلة[عدل]
لتوزيع شحنة، فإن تكامل على المنطقة المحتوية على الشحنة يناظر تجميع لانهائي، يعامل كل عنصر متناهي الصغر من الفراغ كشحنة نقطية .
لتوزيع خطي لشحنة (وهو تقريب جيد لشحنة في سلك) حيث تعطي الشحنة لوحدة طول عند الموقع ، و هي عنصر طول متناهي الصغر،
.
لتوزيع سطحي لشحنة (وهو تقريب جيد لشحنة من طبق على (مكثف) طبق آخر موازي) حيث تعطي الشحنة لوحدة المساحة عند الموقع , and هي عنصر مساحة متناهي الصغر،
لتوزيع حجمي لشحنة (مثلما هو الحال لشحنة داخل كتلة معدنية) حيث تعطي الشحنة لوحدة الحجم عند الموقع ، و هي عنصر حجم متناهي الصغر،
القوة على شحنة اختبار صغيرة عند الموقع هي
التجاذب والتنافر[عدل]
إذا كانت الشحنتان متشابهتان بالنوع فتكون القوة المتبادلة بينهما تنافر وإذا كانت الشحنتان مختلفتان بالنوع تكون القوة تجاذب.
وإذا أردنا أن نحسب المحصلة الكلية لعديد من القوى الناشئة عن أكثر من شحنة نقوم بدراسة تاثير كل شحنة على الشحنات الأخرى وثم نقوم بتحليل تلك القوى الناشئة تحليل اتجاهي وثم نجمع القوى الواقعة على كل محور. ونأتي بذلك على متجه يمثل محصلة القوي الناشئة عن توزيع الشحنات في توزيع معين.
استخدام التكامل للتوزيع النتصل يكون مفيد لايجاد المحصلة بسهولة وهذا القانون تم استنتاجه عن طريق التجربة وليس الاستنتاج الرياضي.
جدول الكميات المشتقة[عدل]
| خاصية الجسيم | العلاقة | خاصية المجال | |||||
| كم المتجه |
|
| |||||
| العلاقة | |||||||
| قيمة عددية |
|
|
مراجع[عدل]
- ^ Current practice is to use c0 to denote the speed of light in vacuum according to أيزو 31. In the original Recommendation of 1983, the symbol c was used for this purpose and continues to be commonly used. See NIST Special Publication 330, Appendix 2, p. 45 [وصلة مكسورة] نسخة محفوظة 22 يونيو 2017 على موقع واي باك مشين.
| في كومنز صور وملفات عن: قانون كولوم |





































