معادلة الاستمرارية
| الميكانيكا التقليدية |
|---|
| تاريخ الميكانيكا التقليدية |
| بوابة الفيزياء |
معادلة الاستمرارية أو معادلة الاستمرار أو معادلة الاتصال هي معادلة تفاضلية لوصف تدفق كمية فيزيائية محفوظة مثل دراسة الكتلة والشحنة الكهربائية وتجد تطبيقاتها في مجال جريان الموائع وفيزياء أشباه الموصلات والنظرية النسبية والكهرومغناطيسية وأخيرا ميكانيكا الكم.[1][2][3]
الصورة العامة[عدل]
الصورة العامة لمعادلة الاستمرارية هي معادلة تفاضلية بالصورة:
حيث:
- الكمية الفيزيائية ولتكن الشحنة الكهربائية.
- رمز تباعد في حسبان المتجهات.
- هي مجال متجهي يصف انسياب الكمية الفيزيائية مثل (التيار الكهربائي).
- معدل التزايد أو التلاشي. ويساوي صفرا لأي كمية فيزيائية محفوظة.
تطبيقات[عدل]
قانون التصريف[عدل]
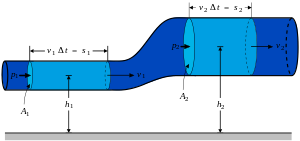
في جريان الموائع، يربط قانون التصريف بين سرعة الانسياب وبين مساحة المقطع العرضي للانبوب، فكلما ضاق الانبوب، ازدادت السرعة، وهذا بديهي. رياضيا:
كتلة المياه الداخلة1 = كتلة المياه الخارجة 2
حجم الداخل1 * الكثافة1 = حجم الخارج2 * الكثافة2
مساحة المقطع1 * المسافة1 * الكثافة1 = مساحة المقطع2 * المسافة2 * الكثافة2
مساحة المقطع1 * سرعة الانسياب1 * الزمن1 * الكثافة1 = مساحة المقطع2 * سرعة الانسياب2 * الزمن2 * الكثافة2
وبما أن الزمن والكثافة متساويين.
إذن:
مساحة المقطع1 * السرعة1 = مساحة المقطع2 * السرعة2 أو:
س1 X ع1 = س 2 X ع 2
الكهرومغناطيسية[عدل]
في الكهرومغناطيسية يمكن صياغة قانون حفظ الشحنة (قانون كيرشوف الثاني) على شكل معادلة مستمرة.
حيث ينص قانون أمبير على أن:
باجراء تباعد للطرفين , ينتج:
و بما أن في كل الأحوال، حيث A يمثل أي مجال متجهي أيا كان. ز هذه إحدى خواص الحسبان المتجهي.
وبما أن قانون قاوس الكهربي ينص على أن:
إذن:
وهذه صيغة مشابهة للصورة العامة لمعادلة الاستمرارية.
انظر أيضًا[عدل]
مراجع[عدل]
- ^ "معلومات عن معادلة الاستمرارية على موقع psh.techlib.cz". psh.techlib.cz. مؤرشف من الأصل في 2019-12-13.
- ^ "معلومات عن معادلة الاستمرارية على موقع wikiskripta.eu". wikiskripta.eu. مؤرشف من الأصل في 2019-12-13.
- ^ "معلومات عن معادلة الاستمرارية على موقع britannica.com". britannica.com. مؤرشف من الأصل في 2016-06-13.