تحليل عدد صحيح إلى عوامل

معضلات لم تحلحل بعد في علم الحاسوب:

هل يمكن تحليل عدد طبيعي إلى عوامل في وقت يتناسب مع قيم متعددة حدود على حاسوب عادي ؟

(لمزيد من المعضلات غير المحلولة (أو المحلحلة) في علم الحاسوب).

مثال توضيحي لتحليل عدد صحيح،
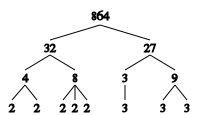
أي أن 864 = 2⁵ × 3³.

في نظرية الأعداد، التحليل إلى العوامل أو تحليل العدد الصحيح أو التفكيك إلى عوامل أولية، هو عملية تفكيكه إلى جداء عوامله الأولية، أي كتابة هذا العدد غير الأولي على شكل جداء أعداد أولية، بحيث يكون حاصل ضربها مساوٍ للعدد الأصلي. مثلا: تحليل العدد 45 هو 3·3·5 أي 3²·5.

أمثلة أخرى:

11 = 11
25 = 5 × 5 = 5²
125 = 5 × 5 × 5 = 5³
360 = 2 × 2 × 2 × 3 × 3 × 5 = 2³ × 3² × 5
1001 = 7 × 11 × 13
1010021 = 17 × 19 × 53 × 59

إذن التفكيك دائما وحيد، وارتباطا مع المبرهنة الأساسية في الحساب. لهذه المعضلة أهمية كبيرة في الرياضيات وفي التشفير وفي نظرية التعقيد وفي الحساب الكمي.

التفكيك إلى أعداد أولية

. 45 = 3²·5 قواسم عدد ما تستنتج من تفكيك هذا العدد. مثلا يعني أن قواسم 45 هي: 3⁰·5⁰, 3⁰·5¹, 3¹·5⁰, 3¹·5¹, 3²·5⁰, و 3²·5¹, أو 1, 5, 3, 15, 9, و 45.

تطبيقات

إذا أخذنا عددين أوليين كبيرين (عدد أرقامهما يفوق 100 رقم) نلاحظ أنه من السهل جدا حساب حاصل ضربهما. لكن العكس صعب جدا يعني أن تفكيك حاصل الضرب الناتج في وقت حدودي غير معروف لحد الآن. هذا المشكل يطبق في الأنظمة الحديثة في مجال تشفير كلمات المرور وغيرها من المعطيات الحساسة. وفي حالة اكتشاف خوارزمية حدودية لحل مشكل التفكيك, ستكون بعض تقنيات التشفير في وضعية صعبة.

بعض خوارزميات التحليل

هناك طرق عديدة تستعمل لتحليل الأعداد الصحيحة، خصوصا عندما يكون العدد كبيرا.

القسمات المتتابعة

تتم بقسمة العدد على التوالي على الأعداد الأولية قسمات تامة والتوقف عند الوصول إلى خارج مساو للعدد 1, أو لعدد أولي.

مثال:
لتحليل العدد الصحيح 180

العدد وناتج القسمة	عدد أولي مقسوم عليه
180	2
90	2
45	3
15	3
5	5
1

أي أن 180 = 2²·3²·5¹

التحليل باستعمال منحنى لنسترا الإهليلجي

انظر إلى تحليل عدد صحيح باستعمال منحنى لنسترا الإهليلجي.

تقارب المربع

لتفكيك عدد, يتم الاستعانة بمفهوم تقارب المربع, فتفكيك العدد a يرجع إلى إيجاد عددين x و y من مجموعة الأعداد الصحيحة الطبيعية، يحققان المعادلة الآتية: x²+a=y². ويكون (a =(x+y)(x-y

انظر أيضًا

• خوارزمية شور.
• فيزياء رياضية
• تحليل إلى عوامل
• جدول القواسم