راديان
| النوع | |
|---|---|
| تستخدم لقياس | |
| رمز الوحدة | |
| رمز يونيكود |
| إلى النظام الدولي |
|---|
| جزء من سلسلة مقالات حول |
| الزوايا |
|---|
 |

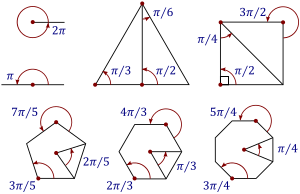
الزاوية نصف القطرية[7] أو الراديان أو التقدير الدائري هي وحدة قياس للزوايا المستوية وهي الوحدة الرسمية المعتمدة ضمن النظام الدولي للوحدات المستخدمة في الرياضيات والفيزياء وتعرف بأنها الزاوية المركزية الموضوعة على مركز الدائرة والتي تحدد قوساً طوله مساوي لنصف قطر الدائرة. يعادل الراديان الواحد درجات، أي بالتقريب .
رسميًا، فإنّ الراديان كمية لا بعدية، بعكس الثانية أو المتر، فهو مجرّد عدد. لذا فإنّ تدوين كلمة راديان (أو rad) هو للإيضاح فقط ويجب ألاّ يفهم منه أنّ له مفهومًا فيزيائيًا. عندما تكتب الزاوية بدون أي علامة، يقصد بشكل عام أن القيمة هي بالراديان، بينما تضاف العلامة للإشارة إلى الدرجة.
إنّ وحدة القياس الرسمية المعتمدة ضمن النظام الدولي للوحدات للزاوية الفراغية الصلبة هي الستراديان، وهي، كذلك مثل الراديان، كميّة لابعديّة لأنها خارج مساحة على مساحة.
تعريف[عدل]
يعرّف الراديان الواحد على أنّه الزاوية المركزيّة في دائرة التي تقابل قوسًا طوله مساوٍ لطول نصف قطر الدائرة.

وبشكل عام، فإنّ مقدار أي زاوية مركزيّة يحصرها نصفا قطر ما بالراديان تساوي النسبة بين طول القوس المقابل للزاوية وبين نصف قطر الدائرة، أي أنّ:
بحيث أنّ:
- هي الزاوية المركزيّة،
- هو طول القوس،
- و هو طول نصف قطر الدائرة.
بالمقابل، فبالإمكان حساب طول قوس في دائرة نصف قطرها يقابل زاوية مركزية مقدارها :
من هذا القانون بالإمكان الاستدلال على مقدار الراديان الواحد. فإنّ زاوية دائرية كاملة تعادل ، وهي تقابل قوسًا يساوي كل محيط الدائرة، لذا فإنّ مقدارها بالراديان هو: . إذا كانت زاوية مقدارها 360 درجة تعادل راديان، فيعادل الراديان الواحد درجة.
تاريخ[عدل]
أوّل من أتى بفكرة الراديان كان الرياضي البريطاني روجر كوتس، عام 1714. مع أنّه لم يطلق على الفكرة كلمة راديان، فقد فهم كوتس مدى بديهيّة المفهوم كوحدة للقياس الزاوي.
تحويل بين الراديان والدرجة[عدل]
للتحويل من راديان إلى درجات يجب أن نضرب الراديان بالقيمة . فعلى سبيل المثال:
وبالمقابل، فللتحويل من درجات إلى راديان، يجب أن نضرب بالقيمة :
إمكانيّة أخرى هي تحويل مقدار الزاوية بالراديان إلى عدد الدورانات بواسطة القسمة على . فمثلاً، إنّ تعادل ثلاثة دورات كاملة.
| جزء الدائرة | ||||||||
|---|---|---|---|---|---|---|---|---|
| الزاوية بالدرجات | ||||||||
| الزاوية بالراديان |
التحليل البعدي[عدل]
كثيرًا ما يستخدم الراديان كوحدة القياس المفضّلة في العديد من المجالات. ففي حساب التفاضل والتكامل، مثلاً، يساعد كون الراديان كميّة غير بعديّة في صياغ المعادلات والبراهين، وهذا بسبب عدم وجود حاجة إلى «إلغاء» وحدة القياس.
إنّ استعمال الراديان، خاصّة في الدوال المثلثية كالجيب وجيب التمام وغيرها، هو بسيط. فمثلاً بواسطة الراديان بالإمكان برهنة نهاية الدالة الآتية:
وهي نتيجة أساسيّة. كذلك، بالإمكان برهنة عدد من المعادلات المثلثية:
بسبب مثل هذه الخواص وغيرها، قد تظهر الدوال المثلثية بالتمثيل الرادياني في سياقات قد لا تمت بصلة مباشرة للمفهوم الهندسي الأصلي لتلك الدوال. فمثلاً، تكون هذه الدوال حلاًّ للمعادلة التفاضلية التالية: .
طريقة أخرى لرؤية الفائدة من وراء كون الراديان كميّة لا بعدية تظهر عند التمعن بمتسلسلة تايلور للدوال المثلثيّة:
فإذا لم يكن الراديان كميّة غير بعديّة، لما كان بإمكان متسلسلة تايلور أن تكتب بهذه البساطة، إذ كان يتوجّب إلغاء البعد الفيزيائي للكمية لكي نتمكن من جمع كل الحدود، لأنّ كل منها بقوّة مختلفة. فلا يمكن أن نجمع حدًا بُعده متر وحدًا بُعده متر.
الاستعمال في الفيزياء[عدل]
إنّ استعمال وحدة الراديان في الفيزياء أمر شائع لقياس الزوايا. فعلى سبيل المثال، تقاس السرعة الزاوية في غالب الأحيان بوحدات راديان في الثانية (). وإنّ وحدة الدورة في الثانية تعادل في الثانية. كما ويقاس التّسارع الزاويّ بشكل عام بوحدة الراديان في الثانية في الثانية ().
يعود سبب الاستعمال الشائع للراديان في الفيزياء إلى نفس أسباب استعماله في الرياضيات - فإنّ استعمال الكمية يبسط الأمور في الكثير من الأحيان.
انظر أيضًا[عدل]
مراجع[عدل]
- ^ أ ب ت مذكور في: ISO 80000-1:2009 Quantities and units—Part 1: General. الصفحة: 18. قسم أو آية أو فقرة أو بند: 6.5.3. الناشر: المنظمة الدولية للمعايير. لغة العمل أو لغة الاسم: الإنجليزية. تاريخ النشر: 15 نوفمبر 2009.
- ^ ويليام فيليبس (18 ديسمبر 2014). "Dimensionless units in the SI". Metrologia: 40–47. DOI:10.1088/0026-1394/52/1/40.
- ^ مذكور في: SI Brochure (9th edition). الناشر: المكتب الدولي للأوزان والمقاييس. لغة العمل أو لغة الاسم: الإنجليزية. تاريخ النشر: 2019.
- ^ مذكور في: SI Brochure (9th edition): Concise summary. لغة العمل أو لغة الاسم: الإنجليزية. تاريخ النشر: 2019.
- ^ مذكور في: أنطولوجية وحدات القياس 1.8.
- ^ مذكور في: ISO 80000–3:2006 : Grandeurs et unités - Partie 3 : Espace et temps. قسم أو آية أو فقرة أو بند: 3-5.a. الناشر: المنظمة الدولية للمعايير. لغة العمل أو لغة الاسم: الإنجليزية. تاريخ النشر: 1 مارس 2006.
- ^ قاموس المورد، البعلبكي، بيروت، لبنان.
| في كومنز صور وملفات عن: راديان |

















































