الجذر التربيعي ل 2
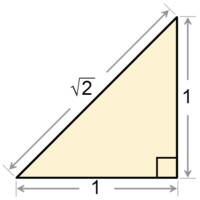
الجذر التربيعي للعدد 2 هو ثابت رياضي، والمعروف أيضا باسم ثابت فيثاغورس، وهو العدد الموجب الذي إذا ضُرب بنفسهِ كانت النتيجة مساوية ل 2.[1][2][3]
يُحتمل أن يكون أول عدد عُرف أنه غير جذري. هندسيا هو وتر المثلث القائم الذي طول كل ضلع من أضلاعه القائمة مساو ل1. أمكن ايجاد الجذر التربيعي ل2 وذلك بفضل مبرهنة فيثاغورس.
وتبلغ قيمته حتى الرقمِ العشريِ الخامس والستين هي:
1.41421356237309504880168872420969807856967187537694807317667973799
وتقريبه بالكسر يساويه حتى المنزلة العشرية الرابعة.
تاريخ الجذر التربيعي للعدد 2[عدل]

التقريب الأول لهذا العددِ وُجِدَ على لوح نحاسي بابلي (1800 حتي 1600 قبل الميلاد) يعطي تقريب ل حتى 4 خانات عشرية :
كما وُجِدَ هذا العددِ في النصوصِ الرياضيةِ الهنديةِ القديمةِ (800-200 قبل الميلاد)والمدعو "شولبا سوترا"، والتي عبّرت عن كالتّالي:
التقريب الهندي القديم عبارة عن الحد السابع بمتوالية فيل، الاعداد التي تلي هذا الحد بمتوالية فيل تعطي تقريب أفضل ل .
إن اكتشاف الأعداد غير النسبية كان على يد هيباسوس، وهو من أتباع المدرسة الفيثاغورية (أتباع فيثاغورس)، وهو بدورهِ وجد أن هو عدد غير نسبي.
طرق لحساب الجذر التربيعي للعدد 2[عدل]
هناك طرق عديدة لايجاد الجذر التربيعي للعدد 2 منها: طريقة ايجاد الجذر التربيعي، احداها هي الطريقة البابلية. طريقة أخرى هي الاستعانة بمتوالية فيل (كلما تقدمنا بايجاد الحدود وجدنا ان القيمة تقترب أكثر وأكثر إلى القيمة الدقيقة للجذر التربيعي للعدد 2)، يمكن التغبير عن ذلك بواسطة الكسر:
من هذا الكسر نتوصل إلى المتوالية تقريبات كسرية هي: .
في سنة 1996 تم التوصل إلى 137,438,953,444 (כ-137.4 مليارد) منازل بعد الفاصلة العشرية للجذر التربيعي للعدد 2, على يد الرياضي الياباني، ياسوما قانادا. في سنة 2006 حطم الرقم القياسي وتوصلوا إلى المنزلة ال200 مليارد بعد الفاصلة العشرية. والحساب كان عن طريق أجهزة الحاسوب واستمر لمدة 13 يوم و14 ساعة.
براهين على أنه عدد غير كسري[عدل]
الجذر التربيعي لاثنين عدد غير كسري. أي أنه لا ينتمي إلى مجموعة الأعداد الكسرية. هناك العديد من البراهين اللائي يثبتن ذلك.
استخدامات[عدل]
من أجل أن تكون النسبة بين ضلعي ورقة دفتر مساوية للنسبة بين ضلعي نصف الورقة يجب على النسبة أن تكون مساوية للجذر التربيعي للعدد 2. لذا قياسات الأوراق المقبولة هي تقريب جيد للجذر التربيعي للعدد 2، فعلى سبيل المثال ورقة الA4 هو 210 على 297 مليمتر يعطي نسبة دقيقة حتى المنزلة العشرية الرابعة للجذر التربيعي للعدد 2.
مراجع[عدل]
- ^ "معلومات عن الجذر التربيعي ل 2 على موقع idref.fr". idref.fr. مؤرشف من الأصل في 2019-03-12.
- ^ "معلومات عن الجذر التربيعي ل 2 على موقع catalogue.bnf.fr". catalogue.bnf.fr. مؤرشف من الأصل في 2019-05-05.
- ^ "معلومات عن الجذر التربيعي ل 2 على موقع mathworld.wolfram.com". mathworld.wolfram.com. مؤرشف من الأصل في 2018-12-20.
| في كومنز صور وملفات عن: الجذر التربيعي ل 2 |






