في الرياضيات ، دالة بُول[1] هي دالة
f
(
x
)
=
f
(
x
1
,
⋯
,
x
n
)
{\displaystyle f(x)=f(x_{1},\cdots ,x_{n})}
f
:
{
0
,
1
}
n
→
{
0
,
1
}
{\displaystyle f:\{0,1\}^{n}\to \{0,1\}}
a
∈
{
0
,
1
}
n
{\displaystyle a\in \{0,1\}^{n}}
[2] [3] [4] i إذا يوجد اعداد ثابتة
a
1
,
⋯
,
a
i
−
1
,
a
i
+
1
,
⋯
,
a
n
∈
{
0
,
1
}
{\displaystyle a_{1},\cdots ,a_{i-1},a_{i+1},\cdots ,a_{n}\in \{0,1\}}
f
(
a
1
,
⋯
,
a
i
−
1
,
0
,
a
i
+
1
,
⋯
,
a
n
)
≠
f
(
a
1
,
⋯
,
a
i
−
1
,
1
,
a
i
+
1
,
⋯
,
a
n
)
{\displaystyle f(a_{1},\cdots ,a_{i-1},0,a_{i+1},\cdots ,a_{n})\neq f(a_{1},\cdots ,a_{i-1},1,a_{i+1},\cdots ,a_{n})}
بما أنَّه يوجد
2
n
{\displaystyle 2^{n}}
{
0
,
1
}
n
{\displaystyle \{0,1\}^{n}}
f
:
{
0
,
1
}
n
→
{
0
,
1
}
{\displaystyle f:\{0,1\}^{n}\to \{0,1\}}
2
2
n
{\displaystyle 2^{2^{n}}}
دوال بول المتناظرة [ عدل ] دالة بول نقول عنها متناظرة إذا اعتمدت فقط على عدد ال-1 في المُدخل وليس على مكانها أي على توزيعها على المتغيرات، لذا فانه يوجد
2
n
+
1
{\displaystyle 2^{n+1}}
دالة الحفة (threshold function)
T
h
k
n
(
x
)
=
1
⟺
x
1
+
x
2
+
⋯
+
x
n
≥
k
{\displaystyle Th_{k}^{n}(x)=1\iff x_{1}+x_{2}+\cdots +x_{n}\geq k}
دالة الأكثرية (majority function)
M
a
j
n
(
x
)
=
1
⟺
x
1
+
x
2
+
⋯
+
x
n
≥
⌈
n
2
⌉
{\displaystyle Maj_{n}(x)=1\iff x_{1}+x_{2}+\cdots +x_{n}\geq \left\lceil {\frac {n}{2}}\right\rceil }
دالة الزوجية (parity function)
⊕
n
(
x
)
=
1
⟺
x
1
+
x
2
+
⋯
+
x
n
=
1
(
mod
2
)
{\displaystyle \oplus _{n}(x)=1\iff x_{1}+x_{2}+\cdots +x_{n}=1{\pmod {2}}}
دالة العد (modular function)
M
o
d
k
(
x
)
=
1
⟺
x
1
+
x
2
+
⋯
+
x
n
=
0
(
mod
k
)
{\displaystyle Mod_{k}(x)=1\iff x_{1}+x_{2}+\cdots +x_{n}=0{\pmod {k}}}
ترجمة الخصائص [ عدل ] يمكن ترجمة كل خاصية أو صفة إلى دالة بول ملائمة وهذه الصفة يمكن ان تحقق أو لا، مثال: الصفة «العدد أولي» ملائم للدالة PRIME بحيث:
عدد اولي
P
R
I
M
E
(
x
)
=
1
⟺
∑
i
=
0
n
x
i
⋅
2
i
{\displaystyle PRIME(x)=1\iff \sum _{i=0}^{n}x_{i}\cdot 2^{i}}
ولنترجم خصائص المُخططات (graphs) على المجموعة
[
n
]
=
{
1
,
⋯
,
n
}
{\displaystyle [n]=\{1,\cdots ,n\}}
x
i
j
{\displaystyle x_{ij}}
(
i
,
j
)
∈
E
(
G
)
{\displaystyle (i,j)\in E(G)}
(
n
2
)
{\displaystyle {\binom {n}{2}}}
خاصية مُخطط
f
(
x
)
=
1
⟺
{\displaystyle f(x)=1\iff }
مثال:
دالة المخطط الكامل (the clique function) أو (Clique(n,k : وهذه الدالة تقبل متجه x إذا وفقط إذا Gx يحوي مخطط كامل مع k رؤوس.
مصفوفة بول [ عدل ] مصفوفة بول هي مصفوفة بحيث أنَّ كل الخلايا قيمتها اما 0 أو 1 .
إذا (f(x,y دالة بول مع 2n متغيرات حينها يمكن النظر اليها على انها مصفوفة،A, بكبر
2
n
×
2
n
{\displaystyle 2^{n}\times 2^{n}}
{
0
,
1
}
n
{\displaystyle \{0,1\}^{n}}
عمليات بول [ عدل ] عمليات بول الأساسية هي:
عملية النقض (negation) ويرمز لها ب- NOT :
¬
x
=
1
−
x
{\displaystyle \neg x=1-x}
x
¯
{\displaystyle {\bar {x}}}
عملية الضم (conjuction), ويرمز لها ب- AND :
x
∧
y
=
x
⋅
y
{\displaystyle x\land y=x\cdot y}
عملية الفصل (disjunction), ويرمز لها ب- OR :
x
∨
y
=
1
−
(
1
−
y
)
⋅
(
1
−
x
)
{\displaystyle x\lor y=1-(1-y)\cdot (1-x)}
عملية الزوجية (parity), ويرمز لها ب-XOR :
x
⊕
y
=
x
(
1
−
y
)
+
y
(
1
−
x
)
=
(
x
+
y
)
(
mod
2
)
{\displaystyle x\oplus y=x(1-y)+y(1-x)=(x+y){\pmod {2}}}
عملية الاستلزام (implication) وهي
x
→
y
=
¬
x
∨
y
{\displaystyle x\to y=\neg x\lor y}
من هذه العمليات يمكن تركيب دوال بول أكثر تعقيدا من دوال بسيطة.
مثال:
لنفرض أنَّ
f
(
x
,
y
)
=
¬
x
+
(
x
∨
y
)
{\displaystyle f(x,y)=\neg x+(x\lor y)}
f
′
(
x
,
y
,
z
)
=
¬
f
(
x
,
y
)
∧
z
{\displaystyle f'(x,y,z)=\neg f(x,y)\land z}
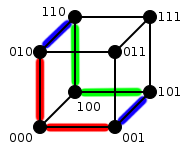
المكعب الثنائي [ عدل ] المعكب الثنائي هو مجموعة كل المتجهات (أي
{
0
,
1
}
n
{\displaystyle \{0,1\}^{n}}
2
n
{\displaystyle 2^{n}}
{
0
,
1
}
n
{\displaystyle \{0,1\}^{n}}
n
2
n
{\displaystyle n\ 2^{n}}
مخطط ثنائي . نرمز لمكعب مع
2
n
{\displaystyle 2^{n}}
Q
n
{\displaystyle Q_{n}}
A هو مُكعب جزئي بُعده d هو مجموعة شكلها كالتالي:
A
=
A
1
×
A
2
×
⋯
×
A
n
{\displaystyle A=A_{1}\times A_{2}\times \cdots \times A_{n}}
i هو أحد المجموعات:
{
0
}
,
{
1
}
,
{
0
,
1
}
{\displaystyle \{0\},\{1\},\{0,1\}}
A
i
=
{
0
,
1
}
{\displaystyle A_{i}=\{0,1\}}
كل دالة بول
f
:
{
0
,
1
}
n
→
{
0
,
1
}
{\displaystyle f:\{0,1\}^{n}\to \{0,1\}}
Q
n
{\displaystyle Q_{n}}
G
f
{\displaystyle G_{f}}
G
f
{\displaystyle G_{f}}
الاشكال الطبيعية [ عدل ] هنالك شكلان طبيعيان لدوال بول: CNF , DNF . لعل أكثر الوسائل بديهية لتمثيل دالة بول هو جدول الحقيقة الخاص بالدالة أي قائمة بكل
2
n
{\displaystyle 2^{n}}
(
a
,
f
(
a
)
)
{\displaystyle (a,f(a))}
a
∈
{
0
,
1
}
n
{\displaystyle a\in \{0,1\}^{n}}
متغير بسيط (literal) هو متغير بول أو ضده أي اما ان يكون
x
i
{\displaystyle x_{i}}
¬
x
i
{\displaystyle \neg x_{i}}
x
i
1
=
x
i
{\displaystyle x_{i}^{1}=x_{i}}
x
i
0
=
¬
x
i
{\displaystyle x_{i}^{0}=\neg x_{i}}
a
=
(
a
1
,
⋯
,
a
n
)
{\displaystyle a=(a_{1},\cdots ,a_{n})}
x
i
1
(
a
)
=
{
1
,
if
a
i
=
1
0
,
if
a
i
=
0
,
x
i
0
(
a
)
=
{
0
,
if
a
i
=
1
1
,
if
a
i
=
0
{\displaystyle x_{i}^{1}(a)={\begin{cases}1,&{\mbox{if }}a_{i}=1\\0,&{\mbox{if }}a_{i}=0\end{cases}}\ ,x_{i}^{0}(a)={\begin{cases}0,&{\mbox{if }}a_{i}=1\\1,&{\mbox{if }}a_{i}=0\end{cases}}}
احادي الحدود (monomial) هو AND متغيرات بسيطة، والتعبير (clause) هو or متغيرات بسيطة. مثال:
x
∧
y
∧
¬
z
{\displaystyle x\land y\land \neg z}
x
∨
y
∨
¬
x
∨
z
{\displaystyle x\lor y\lor \neg x\lor z}
DNF هو OR آحاد الحدود و- CNF هو AND تعابير. كل دالة بول (f(x يمكن التعبير عنها بواسطة (DNF D(x أو (CNF C(x :
C
(
x
)
=
⋁
a
:
f
(
a
)
=
1
⋀
i
=
1
n
x
i
a
i
D
(
x
)
=
⋀
b
:
f
(
b
)
=
0
⋁
i
=
0
n
x
i
1
−
b
i
.
{\displaystyle C(x)=\bigvee _{a:f(a)=1}\bigwedge _{i=1}^{n}x_{i}^{a_{i}}\quad D(x)=\bigwedge _{b:f(b)=0}\bigvee _{i=0}^{n}x_{i}^{1-b_{i}}.}
ثنائي دالة البول [ عدل ] لكل دالة بول يمكن تعريف دالة بول أخرى
f
d
{\displaystyle f^{d}}
f
d
(
X
)
=
f
(
X
¯
)
¯
{\displaystyle f^{d}(X)={\overline {f({\overline {X}})}}}
لهذه الدالة عدة تطبيقات بشكل طبيعي منها في نظرية التصويت (voting theory).
لهذه الدالة كثير من الخصال منها:
لنفرض أن f,g هما دالتين بوليتين حينها:
(
f
d
)
d
=
f
{\displaystyle (f^{d})^{d}=f}
(
f
¯
)
d
=
f
d
¯
{\displaystyle ({\overline {f}})^{d}={\overline {f^{d}}}}
(
f
∨
g
)
d
=
f
d
∧
g
d
{\displaystyle (f\lor g)^{d}=f^{d}\land g^{d}}
(
f
∧
g
)
d
=
f
d
∨
g
d
{\displaystyle (f\land g)^{d}=f^{d}\lor g^{d}}
f
≤
g
⟺
g
d
≤
f
d
{\displaystyle f\leq g\iff g^{d}\leq f^{d}}
دوال بول على انها نظام مجموعات [ عدل ] لكل مجموعة جزئية S من المجموعة
{
1
,
2
,
⋯
,
n
}
{\displaystyle \{1,2,\cdots ,n\}}
v
S
{\displaystyle v_{S}}
v
S
(
i
)
=
1
⟺
i
∈
S
{\displaystyle v_{S}(i)=1\iff i\in S}
حينها يمكن تعريف دالة البول على انها علاقة (predicate)
f
:
2
[
n
]
→
{
0
,
1
}
{\displaystyle f:2^{[n]}\to \{0,1\}}
f
:
2
[
n
]
→
{
0
,
1
}
{\displaystyle f:2^{[}n]\to \{0,1\}}
F
f
=
{
S
|
f
(
S
)
=
1
}
{\displaystyle {\mathcal {F}}_{f}=\{S|f(S)=1\}}
دوال بول أحادية التوجه [ عدل ] لكل مُتجهين
x
,
y
∈
{
0
,
1
}
n
{\displaystyle x,y\in \{0,1\}^{n}}
x
≤
y
{\displaystyle x\leq y}
∀
i
x
i
≤
y
i
{\displaystyle \forall ix_{i}\leq y_{i}}
x
≤
y
⇒
f
(
x
)
≤
f
(
y
)
{\displaystyle x\leq y\Rightarrow f(x)\leq f(y)}
f
:
2
[
n
]
→
{
0
,
1
}
{\displaystyle f:2^{[n]}\to \{0,1\}}
f
(
S
)
=
1
{\displaystyle f(S)=1}
S
⊆
T
{\displaystyle S\subseteq T}
f
(
T
)
=
1
{\displaystyle f(T)=1}
امثلة لدوال احادية الاتجاه هي AND OR , دالة الحفة
T
H
k
n
(
x
)
{\displaystyle TH_{k}^{n}(x)}
انظر أيضا [ عدل ] المراجع [ عدل ] Stasys Jukna , "Boolean Function Complexity:Advances and Frontiers", Springer مقالات رئيسية مفاهيم مفتاحية جدليات شخصيات أساسية قوائم















![{\displaystyle [n]=\{1,\cdots ,n\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fac2ef7727376950b70d6f500a5e9a2998c25336)







































![{\displaystyle f:2^{[n]}\to \{0,1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb90ab65001d743668e6372627e53fc155b1cf2f)
![{\displaystyle f:2^{[}n]\to \{0,1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a78b3cefe46ebd7cc41cebaa9ad421ed8c6cbfd)








