جيب (رياضيات)
| الجيب | |
|---|---|
تمثيل دالة الجيب في جملة الإحداثيات الديكارتيّة
| |
| تدوين | أو جا (س) أو جب (س) |
| تعريف الدالة | sin A = الضلع المقابل لزاوية في مثلث قائمالوتر |
| دالة عكسية | |
| مشتق الدالة | |
| مشتق عكسي (تكامل) |
|
| الميزات الأساسية | |
| زوجية أم فردية؟ | فردية |
| مجال الدالة | |
| المجال المقابل | |
| دورة الدالة | 2π |
| قيم محددة | |
| القيمة/النهاية عند الصفر | 0 |
| الحدود الأعلى | |
| الحدود الأدنى | |
| جذور الدالة | |
| نقاط حرجة | |
| نقاط ثابتة | 0 |
| ملاحظات | |
| تعديل مصدري - تعديل | |
في الرياضيات، جَيْب الزاوية (بالإنجليزية: Sine of an angle) هو أحد الدوال المثلثية الرئيسية، وهو طول الضلع المقابل لهذه الزاوية مقسوما على طول الوتر في مثلث ذي زاوية قائمة، حيث يكون الوتر هو الضلع المقابل للزاوية القائمة. ويرمز له بالرمز (جا) أو (حا) أو (بالإنجليزية: sin).
في المثلث القائم في الشكل حيث يُرمز للوتر (الضلع الأكبر في المثلث) بالرمز c. فيكون تعريف جيب الزاوية A كالآتي:
جيب الزاوية A = الضلع المقابل ÷ الوتر (أي نسبة الضلع a إلى الضلع c).
في الرياضيات وفي الفيزياء وفي الهندسة، تعتبر التوابع المثلثية أو الدوال المثلثية دوالا لزاوية هندسية من أهم الدوال المستخدمة فيها. وهي دوال تتردد في صيغ كثيرة جدا في العلوم ولا مجال لتقدم العلوم بدونها. ومن دراسة حساب المثلثات يمكن وصف ظواهرِ دورية مثل حساب أفلاك الكواكب في الفلك وحسابات التيار المتردد في الهندسة الكهربائية وغيرها.
يمكن تعريف هذه الدوال نسبة بين أضلاع مثلث قائم يَحتوي تلك الزاويةَ أَو بشكل أكثر عمومية إحداثيات على دائرة واحدية.
الدوال المثلثية هي دوال ترتبط بالزاوية، وهي مهمة في دراسة المثلثات وتمثيل الظواهر الدورية المتكررة كالموجات. ويمكن تعريف الدوال المثلثية على أنها نسب بين ضلعين في مثلث قائم فيه الزاوية المعنية، أو بشكل أوسع نسبةً بين إحداثيات نقاط على دائرة الوحدة، ويعتبر دوما عند الإشارة إلى المثلثات أن الحديث يدور حول مثلث في سطح مستوي (مستوى إحداثي أو إقليدي)، وذلك ليكون مجموع الزوايا 180 درجة دائما.
أصل التسمية
[عدل]استعيرت كلمة جيب من لفظ في لغة هندية قديمة تعرف بالسنسكريتية هو jīvā بمعنى وتر وكانت ترادفها أيضاً كلمة jyā في تلك اللغة والتي استعملت في الأصل لوصف وتر قوس المحارب. يقال أن الكلمة jīvā استعيرت إلى العربية «جيبا» أثناء ترجمة العرب للكتب الهندية حيث كان فيهم علماء مولعين بالرياضيات.[بحاجة لمصدر]
الدوال الرئيسية للمثلث القائم
[عدل]هناك ثلاثة دوال مثلثية أساسية هي:
- جا أو جيب الزاوية A = النسبة بين الضلع المقابل للزاوية a مقسوما على الوتر c.
- جتا أو جيب التمام الزاوية A = النسبة بين الضلع المجاور للزاوية a مقسوما على الوتر c.
- ظا أو ظل الزاوية A = النسبة بين الضلع المقابل للزاوية a والضلع المجاور لها b.
تأطيره
[عدل]بصفة عامة، قيمة جيب الزاوية محصورة بين 1- و1، وكذلك قيمة جيب تمام الزواية. و بصفة خاصة، جيب الزاوية الحادة محصور بين 0 و1، وكذلك جيب التمام لها.[1]
تطبيق في الهندسة
[عدل]
بواسطة تعريف جيب الزاوية يمكن حساب الارتفاع في المثلث ABC بالمتر حيث:
- متر
- والزاوية :
مثلما في المثال السابق يمكن حساب الأطوال (والارتفاعات) سواء كانت المقاييس المستخدمة بالمتر أو سنتيمتر أو كيلومتر.
قانون الجيب
[عدل]ينص قانون الجيب على أنه: في أي مثلث أضلاعه هي a وb وc والزوايا المقابلة لهذه الأضلاع هي A وB وC على الترتيب يكون:
أو يمكن صياغته بالشكل التالي:
حيث R هو نصف قطر الدائرة المحيطية لهذا المثلث.
خصائص دالة الجيب
[عدل]دورية
[عدل]دالة الجيب هي دالة دورية دورها 2π.
هذه الخاصية تتدفق بشكل طبيعي من التعريف انطلاقا من دائرة الوحدة. بتعبير أدق، هناك رقمان حقيقيان لهما نفس الجيب إذا كان مجموعهم أو فرقهم ينتمي إلى .
فردية
[عدل]دالة الجيب هي دالة فردية أي:
- .
دالة عكسية
[عدل]دالة الجيب هي دالة دورية وبالتالي غير تباينية. أيضا، نعتبر اقتصارها إلى [- π2,π2] التي هي تقابلية عند نفس المجال في المدى [-1,1] ، ثم نعرف دالتها العكسية، قوس الجيب:
التي تحقق:
- ;
مشتق
[عدل]مشتق الدالة هو دالة جيب التمام.
.
مشتق عكسي
[عدل]- .
نهايات
[عدل]من أجل إلى كل عدد حقيقي x، تكون دالة الجيب مستمرة عند النقطة a، لذلك تكون النهاية في هذه النقطة هي sin (a)، بتعبير آخر:
أما بالنسبة لنهاية الدالة عند ±∞، فهي غير موجودة بسبب دورية الدالة.
الشكل الأسي للدالة
[عدل]- لدينا:
من تلك الصيغ (صيغ أويلر)، يمكن كتابة دالة الجيب على هذا الشكل:
حيث i هي الوحدة التخيلية التي مربعها يساوي الواحد، بتعبير آخر: ، و هي دالة الجيب الزائدية.
تعريف بواسطة الجداء الخارجي
[عدل]في هندسة المتجهات، يُعرَّف الجيب انطلاقا من الجداء الخارجي للمتجهتين و ومعاييرها و بواسطة:
حيث هو مقدار الجداء المتجهي (أو الجداء الشعاعي) للمتجهتين.
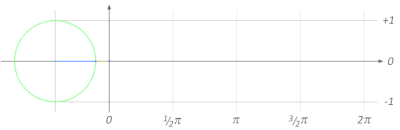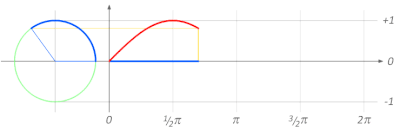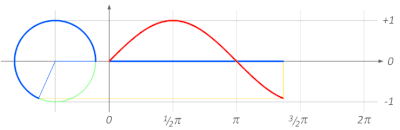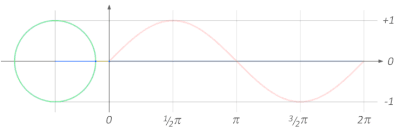
دائرة الوحدة
[عدل]لحساب جيب الزاوية عندما تتغير الزاوية A بين 0 و360 درجة يمكن استخدام دائرة الوحدة. تستخدم تلك الطريقة كثيرا في الفيزياء والفلك والهندسة الكهربائية. وتفسح دائرة الوحدة المجال لحساب الدوال الموجية، ونبين هنا رسما بيانيا لما يسمى الموجة الجيبية.

التعريف باستعمال المتسلسلات غير المنتهية
[عدل]
يمكن التعبير عن جيب الزاوية لزاوية x -معبرا عنها بالتقدير الدائري- بواسطة سلسلة تايلور التالية:

إذا كانت الزاوية مقاسة بالدرجات فسوف تحتوي السلسلة علي كسور مكونة من قوي «ط» مقسومة علي 180 كالتالي:
الكسور المستمرة
[عدل]كما يمكن التعبير عن جيب الزاوية x بواسطة الكسر المستمر المعمم التالي:
التاريخ
[عدل]يقال أن أول من اكتشف دالة الجيب هو الرياضياتي الهندي أريابهاتا، كان ذلك في القرن السادس ميلادي.
أول من نشر المختصرات sin و cos و tan هو عالم الرياضيات الفرنسي ألبرت جيرارد ولقد كان ذلك في القرن السادس عشر.
العلاقة مع الأعداد المركبة
[عدل]
.
دالة الجيب لعدد مركب (عقدي)
[عدل]
قيم الجيب لبعض الزوايا
[عدل]
| x (الزاوية) | جيب الزاوية x | |||
|---|---|---|---|---|
| درجات | دائري | غراد | القيمة بالضبط | بالنظام العشري |
| 0° | 0 | 0g | 0 | 0 |
| 180° | 200g | |||
| 15° | 162⁄3g | 0.258819045102521 | ||
| 165° | 1831⁄3g | |||
| 30° | 331⁄3g | 0.5 | ||
| 150° | 1662⁄3g | |||
| 45° | 50g | 0.707106781186548 | ||
| 135° | 150g | |||
| 60° | 662⁄3g | 0.866025403784439 | ||
| 120° | 1331⁄3g | |||
| 75° | 831⁄3g | 0.965925826289068 | ||
| 105° | 1162⁄3g | |||
| 90° | 100g | 1 | 1 | |
مراجع
[عدل]انظر أيضًا
[عدل]| في كومنز صور وملفات عن: جيب |






![{\displaystyle \mathbb {R} =]-\infty ,+\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f590c037c778e463cee7a4cdde3bb355165f4072)
![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)














![{\displaystyle {\begin{matrix}\mathrm {arcsin} :&[-1,1]&\to &[-{\frac {\pi }{2}},{\frac {\pi }{2}}]\\&x&\mapsto &\arcsin x\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ead01c0ab4a1f33469eeb5b4ad8d069faf04d8cb)
![{\displaystyle \forall x\in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]\quad \arcsin(\sin x)=x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7ab59475d63b3411af27980cdc7fd402c9ca87a)
![{\displaystyle \forall x\in [-1,1]\quad \sin(\arcsin x)=x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50c0ca9887ceb4cb8e2dbe9ed33b84db5ae826a6)



![{\displaystyle {\begin{aligned}e^{i\theta }&=\cos \theta +i\sin \theta \\[5pt]e^{-i\theta }&=\cos \theta -i\sin \theta .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b55517104c78856e37c60ba04ac30cabda0991d7)










![{\displaystyle {\begin{aligned}\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[8pt]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1},\\[8pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d750b214306980413f88142bf78e7556b24f8d8)






















