دوال مثلثية
| جزء من سلسلة مقالات حول |
| حساب المثلثات |
|---|
 |
| بوابة رياضيات |
في الرياضيات، الدَّوَالّ المُثَلَّثِيَّة[عر 1][عر 2] أو التَوَابِع المُثَلَّثِيَّة[عر 3] أو الدَّوَالّ المُثَلَّثَاتِيَّة[عر 4][عر 5][عر 6] أو الدَّوَالّ الدَائِرِيَّة[عر 4][عر 5] (بالإنجليزية: Trigonometric Functions) هي مجموعة من الدوال الحقيقيةٌ التي تربط زاوية مثلث قائم مع نسبة ضلعين من أضلاعه.[1] من الدوال المثلثيةِ الشهيرة والرئيسة دالة الجيب ودالةُ جيبِ التمام، ودالة الظل. مقاليب هذه الدوال هي دوالٌ مثلثيّةٌ أيضاً وهي: قاطع التمام والقاطع وظل التمام على التوالي.
يعود حساب المثلثات إلى ما قبل الميلاد، تحديداً في مصر القديمة واليونان القديمة. وضع الرياضياتي طاليس مبرهنة طاليس في مصر في القرن السادس قبل الميلاد، ووضع الرياضياتي فيثاغورس مبرهنة فيثاغورس، حيث يشار إلى هاتين المبرهنتين بأنهما حجر الأساس لحساب المثلثات. بالإضافة إلى مصر واليونان، حقق علماء الحضارات الأخرى، بما في ذلك الصين والهند والدول الإسلامية والدول الأوروبية، تقدمًا ملحوظًا في علم المثلثات؛ فبرز الخوارزمي والبتاني وأبو الوفاء محمد البوزجاني وشين كوا وغوا شوجينغ وغيورغ يواخيم ريتيكوس وغيرهم.
يُمكن تعريفُ هذه الدوالِ على أنّها نسبةٌ بين أضلاعِ مُثلثٍ قائمٍ يَحتوي تلك الزاويةَ أَو بشكل أكثر عموميةٍ، إحداثياتٍ على دائرة الوحدة. عند الإشارة إلى المثلثات، غالباً يُقصدُ المثلثُ في السَطح المستوي. وذلك ليكون مجموعُ الزوايا °180 دائماً.
توجد تعاريف أخرى للدوال المثلثية، بما في ذلك التعريف بواسطة التكاملات ومتسلسلات القوى والمعادلات التفاضلية، لكل منها تطبيقه الخاص. على سبيل المثال، في التعريف بواسطة متسلسلة القوى، تُستخدم متسلسلة تايلور أو لوران على نطاق واسع في حساب القيم التقريبية للدوال. تسمح بعض التعريفات بتمديد مجال الدوال المثلثية الست إلى المستوي المركب.
يكون متغير الدوال المثلثية عموما زاويةً وقد يكون أيضا عددًا حقيقيًا. كل دالة لديها خصائصها، بما في ذلك الزوجية والفردية، والدورية والاستمرارية والتعامد. التطبيق الرئيسي لهذه الدوال هو حساب أطوال الأضلاع وزوايا المثلث والعوامل الأخرى ذات الصلة. يستخدم هذا التطبيق على مدىً واسعٍ في علوم مختلفة مثل علم المساحة والملاحة ومجالات الفيزياء المختلفة. في علم المساحة، تتمثل في عملية التثليث التي تستخدم لحساب إحداثيات نقطة معينة والتي تُستخدم حاليًا في القياس البصري الثلاثي الأبعاد [الإنجليزية]؛ وفي الملاحة، في حساب إحداثيات السفن ورسم المسارات وحساب المسافات أثناء الملاحة؛ وفي الجغرافيا، حساب مسافة بين نقطتين على الكرة الأرضية، وتحديد إتجاه القبلة بحساب زاويتها بالنسبة للشمال؛ وفي البصريات، تستخدم أساسا في دراسة ظاهرة انكسار الضوء. الدوال المثلثية دوال دوريَّةٌ، أي أنها تُكرر قيمتها بعد مجال محدد؛ ولهذا فإنها تُستعمل لتمثيل الظواهرِ المتكررة كالموجات وهي الأساس الذي يرتكز عليه تحويل فورييه. عملية فورييه هي عمليةٌ رياضيةٌ تُستخدمُ لتحويل دالّةٍ رياضيةٍ بمتغير حقيقي وذات قيم مركّبة إلى دالّة أخرى من نفس الطراز. تشمل الاستخدامات الأخرى للدوال المثلثية في صناعة الطاقة الكهربائية والاتصالات، ويشمل هذا تطبيق دراسة التيارات المتناوبة والتضمين التي تعتمد على موجات جيبية.
تعريف الدوال[عدل]
يوضح الجدول التالي تسميات مختلفة للدوال الست، بالإضافة إلى التسميات الإنجليزية والفرنسية ومجال تعريفهن ومستقراتهن (المجال المقابل).
| التسمية العربية[عر 2][عر 7][عر 8] | التسمية الإنجليزية[عر 9] | التسمية الفرنسية[عر 9] | التدوين بالحروف العربية[عر 10][عر 11] | التدوين بالحروف اللاتينية | المُنطلق[ملاحظة 1][وب 1] | المستقر[وب 1] |
|---|---|---|---|---|---|---|
| الجَيْب، الجَيْب المستوي | Sine | Sinus | جا، جب | sin | جميع الأعداد الحقيقية (أ.ح.) | [-1، 1] |
| جَيْب التَمَام | Cosine | Cosinus | جتا، تجب | cos | أ.ح. | [-1، 1] |
| الظِل، الظل الأول، الظل القائم أو المنتصب أو المعكوس | Tangent | Tangente | ظا، ظل | tan | أ.ح. ما عدا π/2 +kπ | أ.ح. |
| ظِل التمام، الظل الثاني أو المبسوط أو المستوي | Cotangent | Cotangente | ظتا، تظل | cot [ملاحظة 2] | أ.ح. ما عدا kπ | أ.ح. |
| القاطع، قطر الظل الأول | Secant | Sécante | قا | sec | أ.ح. ما عدا π/2 +kπ | ]-∞ , 1] ∪ [1 , +∞[ |
| قاطع التمام، قطر الظل الثاني | Cosecant | Cosécante | قتا، تقا | csc [ملاحظة 3] | أ.ح. ما عدا kπ | ]-∞ , 1] ∪ [1 , +∞[ |
أصل تسمية الدوال[عدل]

استُمِدّت الكلمة الإنجليزية من الكلمة اللاتينية "Sinus" التي تعني «انحناء، خليج»، وأيضاً «طَوْق الثَوْب: الطية المعلقة للجزء العلوي للّباس الروماني تُوجة»، واختيرت على أنها ترجمة للكلمة العربية الأصيلة «جَيْب» -التي تعني "طوق القميص"- في ترجمات القرن الثاني عشر لأعمال البتاني والخوارزمي إلى اللغة اللاتينية للقرون الوسطى.(101) كان الاختيار مبنيًا على القراءة الخاطئة للكلمة العربية «جَيْب» التي هي تحريف للكلمة جِيبَا التي نشأت في حد ذاتها من الكلمة السنسكريتية जीवा / jīvā التي تُترجَم جنبًا إلى جنب برفقة مرادفها ज्या / jyā إلى «وتر قوس المحارب»؛[3][4] حيث استُعمل مصطلح «جَيْب» في الأصل لوصف خط مستقيم مرسوم عموديًّا من أحد طرفي قوس على خط مستقيم آخر يمر بالطَّرف الآخر، وهو يمثل نصف وتر ضعف القوس؛[عر 12] أما علاقتها بجيب الزاوية، فجيب الزاوية هو عبارة عن مقدار هذا الخط المستقيم في دائرة الوحدة. في القرن الحادي عشر، شرح أبو الريحان البيروني ذلك في كتابه القانون المسعودي:[عر 13]
أما الاسم العربي لدالة الـ«ظل»، فقد جاء من مقدار ما يصنعه ظل المقياس على سطح أفقي في أثناء سقوط الضوء على المقياس بزاوية معيّنة، فيقال أن طول الظل يساوي عدة مرات طول المقياس،[عر 14][3] عند تمثيل الرياضيين المسلمين للدالة على دائرة وحدة اعتمد نصف قطرها مقياسًا، كانت النتيجة خطاً مستقيماً يمُس الدائرة،[عر 14] لهذا السبب، أطلق الغربيون (منهم توماس فينك) على الظل اسم "Tangent" التي أتت من اللاتينية "tangens" التي تعني «يمُس».[5][6]
وفقتً لطريقة دالة الظل، كانت النتيجة هي أن قيمة قُطْر الظِّل (تسمية دالة القاطع في عصر الحضارة الإسلامية) هي عبارة عن خط مستقيم يقطع الدائرة، لذا أطلق الغربيون عليه اسم «secant»؛[6] استمدت هذه الكلمة من اللاتينية "secans" التي تعني «يَقْطَع».[7]
أما عن بادئة -co الموجودة في (Cosine، Cotangent)، فقد عُثر عليها في كتاب العالم إدموند غونتر الذي يحمل عنوان "Triangulorum Canon" (صدر في عام 1620)، والذي يُعَرِّف Cosinus بأنها اختصار لعبارة sinus complementi التي استخدمت للإشارة إلى «جيب الزاوية المتممة لزاوية»، مثلاً يقال في الهندسة أن الزاوية المتممة للزاوية 30 درجة في المثلث قائم الزاوية هي 60 درجة وذلك لأن مجموعهما يعطي 90 درجة؛[8] أما عن التسمية العربية «جيب التمام»، فهي استخدمت للإشارة إلى نفس الشيء، حيث أن كلمة «التمام» عند العلماء تعني شيء متمم؛[3] التسمية العربية واللاتينية أتيا من السنسكريتية कोटिज्या «كُوتِي-جِيَا» بمعنى «جيب القوس المتمم لقوس»، حيث يعني المقطع الأول «سِيَة القَوْس»[عر 15] أو «نهاية» أو «طَرَف» عموماً، ولكنها تعني في حساب المثلثات «متمم القوس» أو بمعنى آخر «القوس المقابل للزاوية المتممة لزاوية»، لأن عند نشأة دوال الجيب وجيب التمام، كانت تعتبر آنذاك دوالاً لأقواس وليست دوالاً لزوايا هندسية.[3][9]
التاريخ[عدل]
العصر القديم[عدل]


عُثر على دليل على استخدام الدوال المثلثية في مختلف المجالات، وخاصة في علم الفلك، في العديد من النصوص التي تعود إلى ما قبل التاريخ، بما في ذلك تلك الموجودة في اليونان ومصر وربما في بلاد الرافدين.
استنادًا إلى أحد التفسيرات للوحة المسمارية بليمبتون 322 (قرابة 1900 قبل الميلاد)، أكد البعض أن البابليين القدماء لديهم جدول القواطع. ومع ذلك، هناك الكثير من الجدل حول ما إذا كان جدول ثلاثيات فيثاغورس، أو حل المعادلات التربيعية، أو جدول مثلثي.[10][11]
تعد مبرهنة طاليس من أقدم الأعمال المتعلقة بحساب المثلثات، درس طاليس في مصر في القرن السادس قبل الميلاد، وتوصل إلى طريقة جديدة لحل مشكلة حساب ارتفاع الهرم خوفو، والتي عرفت فيما بعد باسم مبرهنة طاليس. يمكن اعتبار مبرهنة فيثاغورس أيضا أنها حجر الأساس لحساب المثلثات. أنشأ الفلكي والرياضياتي اليوناني أبرخش (180-125 قبل الميلاد) أول جدول مثلثي، وهو جدول خاص بدالة الوتر، لهذا السبب أطلق عليه اسم «أبي حساب المثلثات». وضع منيلاوس الإسكندري أساسا للمثلثات الكروية.[12] في القرن الثاني ميلادي، أنشأ عالم الفلك اليوناني بطليموس الإسكندري جدولا مثلثيا مفصلا للأوتار في الكتاب 1، الفصل 11 من المجسطي.
الهنود[عدل]

كانت دراسة الدوال المثلثية شائعة أيضًا في الهند. على سبيل المثال، في القرن الرابع والخامس الميلادي، في كتاب «سوريا سِدْهانْتا»، استُخدِم جدول لأنصاف الأوتار بدلاً من جدول الأوتار في علم الفلك التي تعادل حاليا دالة الجيب. عرّفت مجموعة من الكتب العلمية «سِدْهانْتا» أولاً الجيب علاقةً حديثة بين نصف زاوية ونصف وتر، وعرفت أيضًا جيب التمام، وسهم الزاوية (1 - جيب تمامها)، ودالة الجيب العكسية.[12] يمكن إسناد دالة الجيب مع جيب التمام وسهم الزاوية إلى الدوال "جيا" و"كوتي جيا" و"أوتكراما جيا" التي استخدمها الهنود في علم الفلك في الحقبة الجوبتية، عن طريق الترجمة من السنسكريتية إلى العربية.[12]
كان بهاسكارا الثاني، الذي عاش في القرن الثاني عشر، من أوائل الذين حسبوا جيب مجموع زاويتين (sin (a+b)) أو طرحهما (sin (a-b))، كما يأتي:[3]
- sin (a+b) = cos(a).sin(b) + sin(a).cos(b)
خطا مادهافا السانغماغرامي، قرابة العام 1400، خطوات أولى ومهمة في تحليل الدوال المثلثية بدلالة المتسلسلات غير المنتهية، ويُعتقد أنه وضع متسلسلات مادهافا، التي سميت باسمه، قبل قرنين من وضعها في أوروبا.[وب 2]
عصر الحضارة الإسلامية[عدل]



خلال القرن التاسع الميلادي، كانت الدوال المثلثية الست المستعملة في العصر الحديث جزءاً من الرياضيات المستعملة في الحضارة الإسلامية، كما كان قانون الجيب معروفاً، وكان يستعمل في معضلة حل المثلثات.[14] باستثناء دالتي الجيب وجيب التمام التي اعتمدت من الهنود،[ملاحظة 4] اكتُشِفَت الدوال المثلثية الأربع الأخرى من قبل علماء الرياضيات المسلمين، بما في ذلك الظل وظل التمام والقاطع وقاطع التمام؛ حيث تنسب أقدم الأعمال المتبقية إلى الخوارزمي وحبش الحاسب اللذين اعتبرا الدوال الأربعة الأخيرة.[3]
في أوائل القرن التاسع الميلادي، أنتج محمد بن موسى الخوارزمي جداول دقيقة لدوال الجيب والجيب التمام وأول جدول للظلال، كما أنه أنتج نسخة معدلة من زيج السندهند (تتضمن جدولاً للجيوب) التي استعملت لحل المعضلات الفلكية.في القرن نفسه، قام حبش الحاسب بإنتاج أول جدول لظل التمام.(103)[15]
في البداية، عُرّفت الدوال الأربعة الأخيرة بطريقة تختلف عن الرياضيات الحديثة. حيث اعتبرت ظل التمام، التي كانت تسمى «الظل المستوي» أنذاك، طول خيال المقياس العمودي ارتفاعه 12 (أحيانًا 7) أصابع؛ بينما اعتبرت دالة الظل، التي كانت تسمى «الظل المعكوس»، طول خيال المقياس الأفقي؛ في الأصل، استُخدمت هذه المفاهيم للحساب بالمزولة.[عر 16] كان يسمى وترا المثلث القائم (القطعة AO في الصورة المرفقة) «قطر الظل الأول» (في الحالة الثانية) و«قطر الظل الثاني» (في الحالة الأولى) اللذان يطلق عليهما الآن القاطع وقاطع التمام، على التوالي. في القرن العاشر ميلادي، قدم الفيلسوف وعالم الرياضيات الفارابي، في كتابه «شرح كتاب المجسطي»، تعريفات هذه الدوال الأربع بشكل مستقل عن المزولات، وقام بتعريفها مع الجيب وجيب التمام في الدائرة المثلثية البطلمية التي طول نصف قطرها 60 (نصف القطر معبر عنه بالنظام الستيني). وضع محمد بن جابر البتاني العلاقات الأساسية بين الدوال الست في القرن نفسه. وحَّد أبو الوفاء البوزجاني في النصف الثاني من القرن العاشر التوحيد الأخير واستعمل للمرة الأولى دائرة الوحدة لتعريف الدوال المثلثية، كما هو الحال في الرياضيات الحديثة.
اكتشف محمد بن جابر البتاني قانون جيب التمام للمثلثات الكروية.[عر 17] واكتشف أبو الوفاء البوزجاني في القرن العاشر تلك المتطابقات المثلثية في شكلها الحالي، وقد عبَّر الرياضياتيون اليونانيون عنها بدلالة الأوتار:[15]
- sin(a+b) = sin(a)cos(b) + cos(a)sin(b)
- cos(2a) = 1 - sin2(a)
- sin(2a) = 2sin(a)cos(a)
ويقال عنه أنه أول من اكتشف قانون الجيب للمثلثات الكروية، ولكن اختلف المؤرخون حول أول من وضع قانون الجيب للمثلثات الكروية، حيث نُسب هذا القانون إلى كل من: أبو الوفاء البوزجاني وأبو محمود الخجندي ونصير الدين الطوسي ومنصور بن عراق؛[15]
طُوِّرت طريقة التثليث لأول مرة من قبل علماء الرياضيات المسلمين، الذين طبقوها على الاستخدامات العملية مثل مسح الأراضي والجغرافيا الإسلامية،[16] كما وصفها أبو الريحان البيروني في كتابه القانون المسعودي في أوائل القرن الحادي عشر. أدخل البيروني نفسه تقنيات التثليث لقياس حجم الأرض والمسافات بين الأماكن المختلفة.[وب 3] حل عمر الخيام معادلات من الدرجة الثالثة في نهاية القرن الحادي عشر عن طريق الحلول العددية التقريبية التي حصل عليها عن طريق استيفاء الجداول المثلثية. في القرن الثالث عشر، اعتبر نصير الدين الطوسي لأول مرة حساب المثلثات تخصّصًا منفصلاً عن علم الفلك،[17] وذكر في كتابه «شكل القطاع» قانوني الجيب أحدهما للمثلثات المستوية والآخر للمثلثات الكروية، واكتشف قانون الظل للمثلثات الكروية، ولم يتفق المؤرخون حول أول من اكتشف قانون الجيب للمثلثات المستوية، حيث ينسب هذا القانون إلى كل من أبو الوفاء البوزجاني ومنصور بن عراق (تلميذه) ونصير الدين الطوسي.
في القرن الخامس عشر، قام غياث الدين الكاشي بالتعبير عن مبرهنة فيثاغورس المعممة، التي أصبحت تطلق عليها الآن «قانون جيب التمام»، بدلالة جيب التمام بعدما أنشئت جداول لها التي أتاحت له صياغة المبرهنة، والبرهنة عليها في كتابه مفتاح الحساب؛ لذلك، أطلق الفرنسيون على هذا القانون اسم «مبرهنة الكاشي» (بالفرنسية: Théorème d'Al-Kashi) تكريما له؛[18] وقدم بياناً صريحاً لهذا القانون في شكل مناسب للتثليث؛[18][19] مع العلم أن هذه المبرهنة تم التعبير عنها سابقًا من قبل العالم اليوناني إقليدس في كتابه الأصول، ولكن عدم وجود الدوال المثلثية آنذاك وكذلك الجبر أدى إلى استعمال مجموع وفرق المساحات.[18] صاغ الكاشي أيضًا المتطابقة التالية: sin(3Φ) = 3 sin(Φ) - 4sin3(Φ) واستخدمها لحساب جيب الزاوية 1° بوضع Φ = 1° وx = sin (1°) ثم حل المعادلة من الدرجة الثالثة المتحصل عليها، ووصل إلى 16 منزلة عشرية؛ هذه الصيغة معروفة عند الغربيين بـ«صيغة فييت» ونسبوها إلى فرانسوا فييت عن طريق الخطأ، ولكن الكاشي هو أول من اكتشف تلك الصيغة.[20] وضع الرياضياتي وحاكم الدولة التيمورية ألغ بك، جداول دقيقة للجيب والظل ووصل إلى 9 أرقام عشرية بعد الفاصلة في نفس الوقت تقريبًا.
الصينيون[عدل]
لم يدرس العلماء الصينيون حساب المثلثات كثيرًا. درس العالمان الصينيان شين كوا وغوا شوجينغ الدوال المثلثية. على سبيل المثال، في القرن الحادي عشر، وجد شين كوا علاقة تقريبية لحساب طول القوس s بدلالة قطر الدائرة d وعمق القوس v وطول الوتر c:[21]
النهضة الأوروبية وما بعدها[عدل]

كانت أطروحات العالم ريغيومونتانوس وتعليقاته، خاصةً كتابه المعنون كل شيء عن المثلثات (باللاتينية: De triangulis omnimodis) في 1464) على المجسطي لبطليموس، هي أصل نهضة حساب المثلثات في أوروبا.[12] علّق في كتابه عن المثلثات:[17]
استخدم عالم الرياضيات الفرنسي ألبير جيرار (1595 – 1632 م) الاختصارات sin، وcos، وtan للمرة الأولى في كتابه حساب المثلثات (بالفرنسية: Trigonométrie).[وب 4]
ربما كان الكتاب Opus palatinum de triangulis لغيورغ يواخيم ريتيكوس، طالب كوبرنيكوس، الأول في أوروبا الذي عرف الدوال المثلثية مباشرة بدلالة المثلثات القائمة بدلاً من الدوائر، مع جداول لجميع الدوال المثلثية الست؛ أُنهي هذا العمل من قبل طالب ريتيكيوس فالنتينوس أوتو في عام 1596.
استعمل عالم الرياضيات الدنماركي توماس فينك مصطلحي "Tangent" و"Secant" للمرة الأولى في كتابه المعنون الهندسة الدائرية (باللاتينية: Geometria rotundi).[وب 5]
برهن غوتفريد لايبنتس على أن دالة الجيب (sin(x ليست دالة جبرية تتبع x، أي أنها دالة متسامية في مقال نُشر عام 1682م.
كانت معظم مقدمة ليونهارت أويلر في كتاب analysin infinitorum (صدرت في عام 1748) عن تأسيس المعالجة التحليلية للدوال المثلثية في أوروبا، كما عرفها متسلسلاتٍ لانهائية ووضع صيغة أويلر، وعرفها كذلك اختصاراتٍ شبه حديثة (sin, cos, tang, cot, sec, cosec).[12]
في ستينيات القرن الثامن عشر، اخترع الإيطالي فينتشنزو ريكاتي الدوال الزائدية، وهي تلك الدوال التي تشبه لحدٍ كبيرٍ الدوال المثلثية.[22]
الدوال المثلثية التاريخية[عدل]
هناك بعض الدوال الشائعة من الناحية التاريخية، ولكن نادراً ما تستخدم الآن، مثل دالة الوتر والسهم (يطلق عليها أيضا اسم «الجيب المعكوس»(102)) وسهم التمام ونصف السهم،[23] والقاطع الخارجي وقاطع التمام الخارجي.
وحدات قياس الزوايا[عدل]
الدرجة: يعود استخدامها إلى عصور قديمة. تُحسبُ هذه القيمة عن طريق تقسيم دائرة إلى 360 جزءاً متساوياً، يشار إليها بقيمة متبوعة بدائرة صغيرة عليا.
الراديان أو الزاوية نصف القطرية أو التقدير الدائري: يساوي الزاوية المقابلة لقوس طوله مطابق لطول نصف قطر الدائرة، دورة كاملة هي زاوية مقدارها 2π راديان. هناك وحدة مشتقة من الراديان وهي الميليراديان، تُعرَّف على أنها جزء من الألف من 1 راديان؛ تُستَخدَم الميليراديان في ضبط الرؤية عند استخدام السلاح الناري.[24]
الغراد: تعادل 1/400 من قياس الدائرة الكاملة، أو 100 جزء من الزاوية القائمة، يشار إليها بقيمة متبوعة بحرف "g" صغير أعلى.[25]
الدورة: تعادل 360° أو 2π راديان.
دقيقة القوس وثانيته: هي وحدات فرعية للدرجة، تستخدم على مدًى واسع في نظام الإحداثيات الجغرافية.
- دقيقة القوس: تساوي 1/60 درجة أي 0.016°،[ملاحظة 5] يشار إليها بقيمة متبوعة بفاصلة عليا (').
- ثانية القوس: تساوي 1/3600 درجة أي 0.00027°،[ملاحظة 5] يشار إليها بقيمة متبوعة بعلامتي التنصيص (").
| وحدة | مقدار | |||||||
|---|---|---|---|---|---|---|---|---|
| درجة | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| راديان | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| غراد | 0g | 1003g | 50g | 2003g | 100g | 200g | 300g | 400g |
| دورة | 0 | 1/12 | 1/8 | 1/6 | 1/4 | 1/2 | 3/4 | 1 |
راديان مقابل درجات[عدل]
في التطبيقات الهندسية، يكون متغير دالة مثلثية عمومًا هو مقياس الزاوية. لهذا الغرض، كل الوحدات الزاوية مناسبة، وتقاس الزوايا في أغلب الحالات بالدرجات.
لا يكون المتغير زاويةً عند حساب التفاضل والتكامل باستعمال الدوال المثلثية، ولكنه بالأحرى عدد حقيقي. في هذه الحالة، من الملائم أكثر التعبير عن المتغير المثلثي طولَ قوس دائرة الوحدة المحددة بزاوية رأسها مركز الدائرة. لذلك، يُستخدم الراديان وحدةً للزاوية.[26]
تكون الصيغ المستعملة عند حساب المشتقات والتكاملات أبسط عند استعمال الراديان، لذلك فهو المُستعمل عادةً اصطلاحاً، أي إذا وحدة الزاوية غير مُذكورة، فيُفترض أن تكون الراديان.
التعريف باستعمال المثلث قائم الزاوية[عدل]

يوضح الشكل المقابل مثلثًا قائماً يتكون من ثلاثة أضلاع a و b و c وزوايا A و B و C. الزاوية C قياسها 90° وزاويتان أخريان حادتان ومتتامتان، بمعنى آخر، مجموع قياس الزاويتين يساوي 90° أو π/2 راديان.
يسمى الضلع المقابل للزاوية C الوتر (كما هو موضح في الشكل المقابل). عند اعتبار الزاوية A، يسمى الضلعان اللذان يشكلان الزاوية القائمة بالضلع المجاور للزاوية A (الضلع AC) والضلع المقابل للزاوية A (الضلع BC).
تعرف الدوال المثلثية الرئيسة للزاوية A كما يأتي:[عر 2][27]
- جيب الزاوية: هو نسبة الضلع المقابل إلى الوتر. أي حاصل قسمة الضلع المقابل للزاوية على وتر المثلث القائم الزاوية، بمعنى آخر:
- جيب تمام الزاوية: هو نسبة الضلع المجاور للزاوية إلى وتر المثلث، بتعبير آخر:
- ظل الزاوية: هو نسبة الضلع المقابل للزاوية إلى الضلع المجاور لها، أي:
وفقًا للتشابه الهندسي، إذا كان لمثلثين زوايا متساوية، فإن نسبة أضلاعهما متساوية. ونتيجة لذلك، تعتمد الدوال المثلثية التي تمثل النسبة بين طولي ضلعين على مقدار الزاوية فقط، يعني أن الدوال لا تتغير قيمتها مع التغير في طول الأضلاع.
بالنسبة للزاوية B، يمكننا أيضًا حساب الدوال المثلثية. الضلع المجاور للزاوية B (الضلع a) هو الضلع المقابل للزاوية A والضلع المقابل B (الضلع b) هو أيضًا الضلع المجاور لـ A، لذلك يمكن القول أن جيب الزاوية B هي جيب التمام الزاوية A والعكس صحيح. علاقة الجيب وجيب التمام بالزوايا المتتامة رياضيا هي كما يلي:[27]
- sin(A) = cos(B) = cos((π/2) - A) = cos(90° - A)
- cos(A) = sin(B) = sin((π/2) - A) = sin(90° - A)
كلما ازدادت قيمة الزاوية A من صفر إلى 90 درجة، تناقص طول الضلع المجاور تدريجياً ويزداد طول الضلع المقابل. عندما تقترب هذه القيمة من 90 درجة، فإن طول الضلع المجاور يقترب من الصفر. نتيجة لذلك، يؤول جيب تمام الزاوية A إلى الصفر. من ناحية أخرى، فإن طول الضلع المقابل يكون مطابقا للوتر (وفقًا لمبرهنة فيثاغورس، فإن الوتر دائمًا أكبر من الضلعين الآخرين). ونتيجة لذلك، جيب الزاوية A يساوي واحدا. بشكل عام، تتراوح قيمة الجيب وجيب التمام في المثلث القائم، بين الصفر والواحد. يمكن تتبع تغيرات ظل الزاوية بنفس الطريقة. عند حوالي 90 درجة، يؤول ظل الزاوية A إلى اللانهاية، وعندما تقترب من الصفر، تقترب قيمته من الصفر، وبالتالي فإن قيمة ظل الزاوية هي عدد موجب (من الصفر إلى اللانهاية).
يمكن تعريف الدوال المثلثية الثلاث الأخرى بأنها مقاليب الدوال الثلاث المذكورة أعلاه:[27]
- ظل تمام الزاوية: هو نسبة الضلع المجاور إلى الضلع المقابل، أي:
- cot (A) = b/a = cos(A)/sin(A) = 1/tan(A)
- قاطع الزاوية: هو نسبة وتر المثلث إلى الضلع المجاور، أي:
- sec (A) = c/b = 1/cos(A)
- قاطع تمام الزاوية: هو نسبة وتر المثلث إلى الضلع المقابل، أي:
- csc (A) = c/a = 1/sin(A)
نطبق العلاقة بين الزوايا المتتامة، كما هو مذكور أعلاه في حالة الجيب وجيب التمام، أيضًا على الدوال المثلثية الأخرى:[27]
- tan(A) = cot(B) = cot((π/2) - A) = cot(90° - A)
- cot(A) = tan(B) = tan((π/2) - A) = tan(90° - A)
- sec(A) = csc(B) = csc((π/2) - A) = csc(90° - A)
- csc(A) = sec(B) = sec((π/2) - A) = sec(90° - A)
ملخص العلاقات
تُلخص العلاقة بين الدوال المثلثية وأضلاع المثلث القائم بالعلاقات التالية:
- sin (A) = المقابلالوتر
- cos (A) = المجاورالوتر
- tan (A) = المقابلالمجاور
- cot (A) = المجاورالمقابل
- sec (A) = الوترالمجاور
- csc (A) = الوترالمقابل
التعريف باستعمال دائرة الوحدة[عدل]
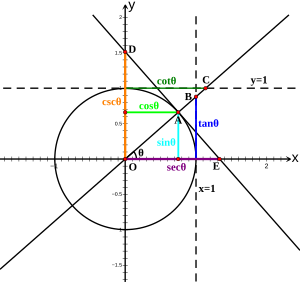


يمكنُ تعريفِ الدوالِ المثلثيةِ: الجيب وجيب التمام والظل ومقلوباتها، بقيمِ إحداثياتِ النقاطِ على المستوى الإقليدي المرتبطةِ بدائرة الوحدة. دائرة الوحدة هي دائرة نصف قطرها وحدةٌ واحدةٌ ومركزها نقطة الأصل. مع أن تعريفات المثلثِ قائمِ الزاوية تسمحُ بتعريفِ الدوالِ المثلثيةِ للزوايا بينَ 0 وπ/2 راديان فقط، إلا أنَّ تعريفاتِ دائرةِ الوِحدةِ تُعمّمُ ذلك وتمدد مجال الدوال المثلثية لتسمحَ بجميع الأعداد الحقيقية الموجبةِ والسالبةِ.
تُعطى تعريفات الدوال المثلثية من تقاطع مستقيمات مرتبطة بزاوية واقعةٍ على نقطة الأصل. إذا قطعَ الشعاعُ المنطلق من نقطة الأصل بزاويةَ θ[ملاحظة 7] دائرةَ الوحدةِ في النقطة A=(x,y) فإنّ الدالةُ cos(θ) تُعرّف على أنها الإحداثي x والدالة sin(θ) هي الإحداثي y لنقطة التقاطع. وبمعنى آخر فإنَّ: (x, y) = (cos(θ), sin(θ)). وبرسم مماسٍ من النقطة (x, y) يقطعُ محورَي السينات والصادات في النقطتين E = (a,0), F=(0,b) على الترتيب، فإنَّ a = sec(θ), b = csc(θ).
يتطابقُ هذا التعريفُ مع تعريفِ المثلث قائم الزاوية في المجال (0, π/2) باعتبار أنَّ نصفَ قطرِ دائرة الوحدة OA = r هو وترٌ للمثلث القائم. ولأنّ كل نقطة P = (x0,y0) على دائرة الوحدة تُحقّق x2 + y2 = 1 من مبرهنة فيثاغورس في المثلث القائم OCA، فإنَّ تعريف الدوال المثلثية على أنها الإحداثيات x, y يُنتِجُ متطابقة فيثاغورس: cos2θ+sin2θ=1. وأخيراً فإنَّ المسافات AF, AE تُعرّفُ على أنّها الدوال المثلثية: cot(θ) وtan(θ) على الترتيب. بشكلٍ مُشابهٍ للاستنتاج السابق، يمكن تطبيق مبرهنة فيثاغورس في بقية المثلثات القائمة OAF وOAE وOEF للوصول إلى متطابقات فيثاغورس الخاصة ببقية المتطابقات المثلثية. ومن تشابه هذه المثلثات القائمة السابقة، تُعطى العلاقات التي تربط بين جميع الدوال المثلثية كالآتي:[وب 6]
بما أنَّ دوراناً بزاوية 2π± لا يُغير موضعَ الشكلِ ولا حجمَهُ، فإن النقاط F, A, E ستبقى نفسها بالنسبة لزاويتين فرقَهُما مضاعف صحيح لـ 2π. وعلى ذلكَ، الدوال المثلثية هن دوالٌ دورية ذات دور 2π. بمعنى آخر، المساواةَ sinθ = sin(θ + 2kπ) وcosθ = cos(θ + 2kπ) محققة أياً كانت قيمة θ زومن أجل أي عدد صحيح k. ينطبق الشيء ذاته على الدوال المثلثية الأربع الأخرى.
تشير ملاحظة إشارة ورتابة دوال الجيب وجيب التمام والقاطع وقاطع التمام في الأرباع الأربعة إلى أن 2π هي أصغر قيمة تكون دورية لها، أي 2π هي الدور الأساسي لتلك الدوال. إلا أن بعد الدوران بزاوية π، تعود النقطتان B وC إلى موضعهما الأصيل ، بحيث تكون دالتا الظل وظل التمام لها دور أساسي π.[عر 2]
الدوران[عدل]
يمكن الحصول على الدوال المثلثية للزوايا الأكبر من 90° باستخدام علاقات الدوران حول مركز الدائرة. أيضًا، يمكن حساب الزوايا الأصغر من الصفر بالانعكاس حول المحور الأفقي. يوضح الجدول التالي كل العلاقات المثلثية:
| انعكاس حول المحور الأفقي[عر 18] | دوران بزاوية π/2 | دوران بزاوية π | دوران بزاوية 2kπ (مع k عدد صحيح) | انعكاس حول المحور العمودي |
|---|---|---|---|---|
| sin(-θ)= -sin (θ) | sin(θ + (π/2))= +cos (θ) | sin(θ + π) = -sin (θ) | sin(θ + 2kπ) = +sin (θ) | sin(π-θ)= sin(θ) |
| cos(-θ)= +cos (θ) | cos(θ + (π/2))= -sin (θ) | cos(θ + π) = -cos (θ) | cos(θ + 2kπ) = +cos (θ) | cos(π-θ)= -cos (θ) |
| tan(-θ)= -tan (θ) | tan(θ + (π/2))= -cot (θ) | tan(θ + π) = +tan (θ) | tan(θ + 2kπ) = +tan (θ) | tan(π-θ)= -tan (θ) |
| cot(-θ)= -cot (θ) | cot(θ + (π/2))= -tan (θ) | cot(θ + π) = +cot (θ) | cot(θ + 2kπ) = +cot (θ) | cot(π-θ)= -cot (θ) |
| sec(-θ)= +sec (θ) | sec(θ + (π/2))= -csc (θ) | sec(θ + π) = -sec (θ) | sec(θ + 2kπ) = +sec (θ) | sec(π-θ)= -sec (θ) |
| csc(-θ)= -csc (θ) | csc(θ + (π/2))= +sec (θ) | csc(θ + π) = -csc (θ) | csc(θ + 2kπ) = +csc (θ) | csc(π-θ)= csc (θ) |
-
رسم دالتي الجيب وجيب التمام باستخدام دائرة الوحدة
-
الدوال المثلثية: الجيب، جيب التمام، الظل، قاطع التمام (متقطع)، القاطع (متقطع)، ظل التمام (متقطع).
القيم الجبرية[عدل]


بالنسبة لبعض الزوايا، يمكن الحصول على قيم الدوال المثلثية بسهولة، تدعى هذه الزوايا: الزوايا الخاصة أو الزوايا الشهيرة.
إذا كان مقدار الزاوية يساوي 0°، فإن جيبها يساوي 0 وجيب التمام يساوي 1. وإذا كان مقدار الزاوية يساوي 90°، يصبح جيب التمام يساوي 0 والجيب يساوي 1، بتعبير آخر:
- sin (0°) = cos (90°) =0
- sin (90°) = cos (0°) =1
المثلث القائم ذو زاوية 45° له زاوية حادة أخرى تبلغ 45° أيضا، يطلق على هذا المثلث اسم مثلث قائم ومتساوي الساقين. في هذا المثلث، بناءً على مبرهنة فيثاغورس، طول الوتر يساوي 2√ مرة طول كل من الساقين، إذن:
sin (45°) = cos (45°) =(√2)/2 tan (45°) = cot (45°) = 1
باستخدام خصائص مثلث متساوي الأضلاع (الشكل المقابل)، يمكن إظهار أن الضلع المقابل للزاوية 30° هو نصف طول الوتر، إذن:
وبالمثل، يُحسب على طول الضلع الآخر باستخدام مبرهنة فيثاغورس، الذي يساوي 3/2√، نتيجة لذلك:
توفر كتابة البسوط باستعمال جذور تربيعية للأعداد الصحيحة غير السالبة مع مقام مساوٍ 2، طريقة سهلة لتذكر القيم.[29]
تنص مبرهنة نيفن على أن القيم الكسرية الوحيدة للزاوية θ التي تتواجد في المجال بين [0° ,90°] والتي يكون جيبها عدداً كسريًا هي الزوايا ذات القيم 0 و30 و90 درجة.[30] تمتد المبرهنة أيضًا إلى الدوال المثلثية الأخرى وإلى بعض من الزوايا.[31] بالنسبة للقيم الكسرية لـ θ، فإن القيم الكسرية الوحيدة للجيب أو جيب التمام هي 0 و (1/2)± و 1±؛ والقيم الكسرية الوحيدة للقاطع أو قاطع التمام هي 1± و 2±؛ والقيم الكسرية الوحيدة للظل أو ظل التمام هي 0 و1±.[32]
مثل هذه التعبيرات البسيطة غير موجودة عمومًا للزوايا الأخرى التي تعتبر مضاعفات كسرية لزاوية مستقيمة. بالنسبة للزاوية التي تقاس بالدرجات، وهي من مضاعفات العدد 3، قد يُعبَّر عن الجيب وجيب التمام بدلالة الجذور التربيعية، ويعني هذا إنشاء الزوايا ذات الصلة بقيم الجيب وجيب التمام باستعمال المسطرة والفرجار.
يمكن التعبير عن جيب زاوية عدد صحيح بالدرجات وجيب تمامها بدلالة الجذور التربيعية والجذر التكعيبي لعدد مركب[ملاحظة 8] غير حقيقي.[وب 7] تسمح نظرية غالوا بإثبات أنه إذا لم تكن الزاوية مضاعف 3°، فإن الجذور التكعيبية غير الحقيقية لا يمكن تجنبها.
بالنسبة للزاوية التي تقاس بالدرجات وهي عدد كسري، الجيب وجيب التمام هما عددان جبريان، يمكن التعبير عنهما بدلالة الجذور النونية.[وب 7]
بالنسبة للزاوية التي تقاس بالدرجات وهي عدد غير كسري، إما أن تكون الزاوية أو الجيب وجيب التمام عددين متساميين. إنها لازمة مبرهنة باكر، أُثبتت في عام 1966.[33]
القيم الجبرية البسيطة[عدل]
يلخص الجدول التالي أبسط القيم الجبرية للدوال المثلثية.[34] يمثل الرمز ∞ النقطة عند اللانهاية على الخط الحقيقي الممتد بشكل إسقاطي؛ إنها غير مؤشَّرة، لأنها عندما يظهر في الجدول، تؤول الدالة المثلثية المقابلة إلى +∞ في جهة، وإلى -∞ في جهة أخرى، عندما يؤول المتغير إلى القيمة في الجدول.
حساب التفاضل والتكامل[عدل]
الدوال المثلثية هي دوال قابلة للتفاضل. هذا ليس واضحا على الفور من التعاريف الهندسية المذكورة أعلاه. علاوة على ذلك، فإن الاتجاه الحديث في الرياضيات هو بناء هندسة رياضية من حساب التفاضل والتكامل بدلاً من العكس. لذلك، باستثناء في المستوى الأساسي، يتم تعريف الدوال المثلثية باستخدام طرق حساب التفاضل والتكامل.
لتعريف الدوال المثلثية داخل حساب التفاضل والتكامل، هناك عدة امكانيات، منها التعريف باستخدام متسلسلة القوى أو المعادلات التفاضلية. هذه التعريفات الأخيرة متكافئة لأن انطلاقا من واحد منهم، من السهل البدء في استرداد التعريفات الأخرى كخاصية. ومع ذلك، يعتبر التعريف من خلال المعادلات التفاضلية أكثر طبيعية إلى حد ما، لأنه على سبيل المثال، قد يبدو اختيار معاملات متسلسلة القوى كله اختياري، ومتطابقة فيثاغورس هي أسهل بكثير لاستنتاج من المعادلات التفاضلية.
الاشتقاق والمكاملة[عدل]
المشتقات الأولى والثانية للدوال المثلثية مع مشتقاتها العكسية هي كما يلي:[35]
التعريف بواسطة التكامل[عدل]
يمكن الحصول على تعريف آخر استناداً إلى الطول الدقيق لقوس الدائرة. باعتبار معادلة النصف الأعلى لدائرة الوحدة ، يمكن إيجاد العلاقة بين الزاوية θ وsinθ وفقًا للمعادلة التالية:[36]
وتنتمي الزاوية θ إلى المجال [0، π/2].
التعريف بواسطة المعادلات التفاضلية[عدل]
- الجيب وجيب التمام هما من الدوال الفريدة من نوعها التي تقبل التفاضل، بحيث:
- كل من دالتي الجيب والجيب التمام تحققان المعادلة التفاضلية التالية: y = -y (معادلتها المميزة هي m2+1 = 0، جذرها هي وحدة تخيلية موجبة أو سالبة i±) بتعبير آخر، كل منهما تساوي مقابل مشتقتها من الدرجة الثانية.
- الجيب هو الحل الوحيد لهذه المعادلة التي تحقق الشروط التالية:[وب 8]
جيب التمام هو الحل الوحيد لهذه المعادلة التي تحقق الشروط التالية:[وب 8]
بتطبيق قاعدة ناتج القسمة على تعريف ظل الزاوية باعتباره نسبة بين الجيب وجيب التمام، يحصل الفرد على أن دالة الظل تحقق:
إذن، دالة الظل هي حل للمعادلة التفاضلية التالية:
- نعتبر المعادلة التفاضلية من الدرجة الثانية التالية:
- إن حل هذه المعادلة هي الدالة الأسية من الشكل ، حيث و هما جذور المعادلة المميزة للمعادلة (). أيضا و هي ثوابت كيفية بناءً على الشروط الأولية.
- إذا كانت المعادلة المميزة لها جذور مركبة، فإن حل هذه المعادلة هي الدالة الأسية المركبة:
- حيث α هو الجزء الحقيقي وβ هو الجزء التخيلي لجذر المعادلة المميزة. استنادًا إلى صيغة أويلر، يمكننا تحويل الدالة الأسية المركبة إلى دالتي الجيب وجيب التمام، لذلك في حالة الجذور المركبة، ستتضمن حل المعادلة التفاضلية دوال مثلثية:
باستعمال المتسلسلات[عدل]



دوال مثلثية هي دوال تحليلية. يمكن تمثيل جميع الدوال المثلثية بواسطة متسلسلات لانهائية.
باستخدام متسلسلة تايلور، يمكن كتابة كل دالة مستمرة على شكل متسلسلة قوة بجوار النقطة a على النحو التالي:[37]
حيث تشير !n إلى عاملي عدد.
عندما يكون a=0، تتحول هذه المتسلسلة إلى متسلسلة ماكلورين، رياضيا:[37]
- ملاحظة: الزاوية x مقاسة بالتقدير الدائري في جميع السلاسل التالية.
متسلسلتا ماكلورين لدالتي الجيب وجيب التمام[عدل]
- جيب الزاوية:[38]
يوضح الشكل المقابل الرسم البياني لدالة الجيب إلى جانب متعدد الحدود السابع لماكلورين. قيمة دالة الجيب عند الصفر تساوي صفر، لذا فإن الحدود الزوجية لمتسلسلة القوة للجيب هي صفر. ونتيجة لذلك، فإن متسلسلة القوة للجيب ستحتوي فقط على حدود فردية.
- جيب تمام الزاوية
وبالمثل، فإن الحدود الفردية لمتسلسلة جيب التمام هي صفر ، وتحتوي المتسلسلة فقط على حدود زوجية.
نصف قطر التقارب[ملاحظة 9] لتلك المتسلسلات غير منتهية. ولذلك، يمكن أن تمدد دالتا الجيب وجيب التمام إلى دوالتي صحيحتين، وهذه بالتعريف، دوال ذات قيم مركبة وتامة التشكل على مجمل المستوي المركب.[39]
متسلسلات القوى لباقي الدوال[عدل]
الدوال المثلثية الأخرى لها مجالات خاصة، لذلك لا يمكن تحديد متسلسلة تايلور لأي قيمة. بالنسبة لدالتي الظل والقاطع غير المعرفة عند π/2 (أو °90)، تكون مجال تعريف متسلسلاتهم بين π/2- وπ/2، لذا، يمكن تمثيل هاتين الدالتين بواسطة متسلسلة ماكلورين. أيضًا بالنسبة لدالتي ظل التمام وقاطع التمام غير المعرفة عند الصفر، تكون مجال تعريف متسلسلاتهم بين 0 وπ وبين π- و0، لذلك، يمكن تمثيلهن بواسطة متسلسلة لوران، هذه الأخيرة، هي تمثيل دالة على شكل متسلسلة القوى ذات درجات سالبة (متسلسلة ذات بعض الحدود المرفوعة لِأُس سالب).
بتعبير أدق،Un هو تبديل متناوب من المرتبة n. وBn هو عدد بيرنولي من المرتبة n، وEn، هو عدد أويلر من المرتبة n.

تُعرف الدوال المثلثية الأربعة الأخيرة على أنها كسور من الدوال الصحيحة. لذلك، يمكن أن تُمدّد إلى دوال جزئية التشكل، والتي هي دوال تامة التشكل في كامل المستوي المركب، باستثناء بعض النقاط المعزولة التي تسمى الأقطاب، وهي في هذ الحالة أعداد من الشكل (π/2)(2k+1) بالنسبة لدالتي الظل والقاطع، أو kπ بالنسبة لدالتي ظل التمام وقاطع التمام، مع k عدد صحيح كيفي.[وب 9]
يمكن أيضًا حساب علاقات الاستدعاء الذاتي لمعاملات متسلسلة تايلور لتلك الدوال. متسلسلاتهما لها نصف قطر التقارب منتهي. معاملاتهم لها تفسير توافيقي: فهي تُعدّد التبديلات المتناوبة للمجموعات المنتهية.
عدد الحدود في متسلسلة القوة المستخدمة لتقريب الدوال غير منتهي، ولكن في الحسابات يُستخدم عدد محدود من تلك الحدود. يطلق على الحدود الأخرى غير المحسوبة اسم الباقي. يُعرَّف الباقي من المرتبة n لمتسلسلة بواسطة:
مع زيادة قيمة x، ستكون هناك حاجة إلى المزيد من الحدود لتحقيق دقة معينة، ونتيجة لذلك، ستنخفض سرعة التقارب. بالإضافة إلى ذلك، فإن الدوال الأربعة الأخيرة لها نقاط عدم الاستمرار (نقاط عدم الإتصال)، ومتسلسلات القوى لهذه الدوال معرفة على مجال معين.
لمنع التقارب من التباطؤ والتخلص من مشكلة نقاط عدم الاستمرار، يجب علينا تقليص الزاوية قدر الإمكان قبل استخدام المتسلسلة. باستخدام متطابقات الزوايا المتتامة، يمكن تقليص الزاوية إلى (0,n/4)، وباستخدام بعض المتطابقات المثلثية إلى (0, n/2). بهذه الطريقة، تزداد سرعة تقارب المتسلسلة والكفاءة الحسابية.
متسلسلات أخرى[عدل]
يوجد تمثيل متسلسلات آخر يتضمَّن مفكوكًا كسريًّا جزئيًّا، وفيه تُجمَع دوال المقلوب المزاحة فقط، فتتطابق أقطاب دالة ظل التمام ودوال المقلوب:[40]
- يمكن إثبات هذه المتطابقة بواسطة حيلة هيرغلوتس [الإنجليزية].[41]
ويمكن بالطريقة نفسها إيجاد المفكوكات الكسرية الجزئية لكل من القاطع وقاطع التمام والظل:

الكسور المستمرة المعممة[عدل]
الكسور المستمرة المعممة هي تعميم للكسور المستمرة الاعتيادية في المجالين الحقيقي والمركب.
يمكننا كتابة الدوال الرياضية على هذا النحو:[42]

في ما يلي الكسور المستمرة لبعض الدوال:

متسلسلة الجداء اللانهائي[عدل]
الجداء اللانهائي التالي لدالة الجيب له أهمية كبيرة في التحليل المركب:[43]
من هذه المتسلسلة، نستنتج أن:[43]
باستخدام المعادلات الدالية[عدل]
يمكن أيضاً تعريف الدوال المثلثية باستخدام المعادلات الدالية المختلفة.
مثلاً،الجيب وجيب التمام هما دالتان فريدتان من الدوال المستمرة التي تحقق صيغة الفرق:
cos(x-y) = cos x.cos y + sin x.sin y
بشرط أن تكون 0 < x > sin(x) > x.cos(x) من أجل 0 < x > 1.
في المستوى المركب[عدل]
يمكن التعبير عن الجيب وجيب التمام لعدد مركب باستعمال دالتي الجيب وجيب التمام مع الدوال الزائدية:
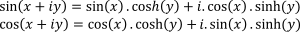
من الممكن أن تمثيل الدوال المثلثية ذات القيم المركبة بيانياً عن طريق التمثيل بتلوين المجال. يمكن مشاهدة العديد من الميزات الفريدة للدوال المركبة من الرسم البياني؛ مثلاً، يمكن اعتبار دالتي الجيب وجيب التمام أنهما غير منتهية عندما يصبح الجزء التخيلي لـ z أكبر (لأن اللون الأبيض يمثل اللانهاية)، وحقيقة أن الدوال تحتوي على أصفار أو أقطاب بسيطة تتضح من حقيقة أن الألوان تدور حول كل صفر أو قطب مرة واحدة بالضبط. إن مقارنة هذه التمثيلات البيانية (بواسطة الألوان) مع تلك التمثيلات الخاصة بالدوال الزائدية توضح العلاقات بينهما.[وب 10]
عند تمثيل الدوال في المستوى المركب، تُمثَّل العمدة بالألوان، والمعيار بوسائل أخرى، مثل السطوع أو الإشباع اللوني.
-
sin z
-
cos z
-
tan z
-
cot z
-
sec z
-
csc z
-
التمثيل البياني للعدد المركب z = x + iy الذي استخدم في التمثيلات البيانية.
الخصائص[عدل]
زوجية وفردية[عدل]
الدوال الزوجية والدوال الفردية هي دوال تحقق شرطاً محدداً يتعلق بالتناظر.
جيب التمام والقاطع دالتان زوجيتان، أما الدوال الأخرى فهي فردية، أي:

دورية[عدل]
الدوال المثلثية كلها دوالٌ دوريةٌ أصغر دور لها هو 2π. باستثناء الظل وظل التمام، التي أصغر دور لها هو π، أي، من أجل عدد صحيح k، يكون:
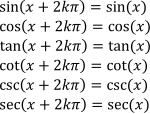
تستخدم خاصية دورية الدوال المثلثية لحل المعادلات التفاضلية في تحويل فورييه والمعادلات الموجية.
استمرارية (اتصال)[عدل]
الجيب وجيب التمام دالتان مستمرتان دومٌا ويمكن اشتقاقهما ويتضح ذلك بوضوح من خلال التعريف باستعمال المثلث القائم وباستعمال دائرة الوحدة. إن الدوال الأخرى، التي مقامها =دالتا الجيب أو جيب التمام، ليست دائمًا مستمرة، لأن قيمة كل من دالة الجيب وجيب التمام في بعض من الحالات تساوي الصفر. نقاط عدم الاستمرار للدوال المثلثية هي كالتالي (حيث k هو عدد صحيح كيفي):
- الظل والقاطع: kπ + {π/2}
- ظل التمام وقاطع التمام: kπ
تعامد[عدل]
تكون دالتا الجيب وجيب التمام متعامدتين، أي:

تستخدم هذه الخصائص لحساب معاملات متسلسلة فورييه.[44]
تحويلا لابلاس وفورييه[عدل]
تحويل لابلاس هو أحد طرق حل المعادلات التفاضلية. تحويلا لابلاس لدالتي الجيب وجيب التمام هي كما يلي:[ملاحظة 10]
- تحويل الجيب:
- تحويل جيب التمام:
تحويلا فورييه لدالتي الجيب وجيب التمام هي كما يلي:[ملاحظة 11]
- الجيب:
- جيب التمام:
دالة ذاتية[عدل]
دالتا الجيب وجيب التمام ذاتيتان لمؤثر لابلاس. على سبيل المثال، إذا كان : Δ=∇2 يُمثِّل مؤثر لابلاس وحيد البعد، فإن دالتا الجيب وجيب التمام تحققان : ، مع λ تمثل قيمة ذاتية؛ ويمكن التحقق من هذه المساواة انطلاقا من التعريف باستعمال المعادلة التفاضلية للدالتين.[45]
حساب القيم[عدل]
حساب القيم الدقيقة للدوال المثلثية يدوياً أمر صعب ومعقد، لكن في العصرِ الحديثِ، زالَت تعقيداته بسبب توفر أجهزة الحاسوب والآلات الحاسبة، التي تمكن بسهولة الحصول على القيمة الدقيقة لأي زاوية. بالنسبةِ لبعضِ الزوايا، فيمكن الحصول على القيم الجبرية الدقيقة لدوالِّها المثلثية دون اللجوء إلى حساباتٍ بالأجهزة، وتُسمّى هذه الزوايا: الزوايا الخاصة. على سبيل المثال، قيمُ الدوال المثلثية لجميع الزوايا من مضاعفات العدد 3 دقيقة. تُحسَبُ النسب المثلثية للزاوية 3° بتطبيق الفرق بين زاويتين ذات القيم 18° و15° (3 = 15 - 18). وتُحسَبُ النسب المثلثية للزاوية 18° باستخدام خواص ونِسَب الخماسي المنتظم.
يلزم لحساب قيمة دالة مثلثية لأي زاوية تقليص مجال الزاوية، مثلاً من الصفر إلى π/2، باستخدام خاصيتي الدورية والتناظر للدوال المثلثية.
حُسِبت قيمة الدوال المثلثية قبل الحواسيب من خلال استيفاء الجداول المثلثية. هذه الجداول لها تاريخ طويل في علم المثلثات.وتُحسب قيم هذه الجداول عادةً عن طريق استخدام متطابقات نصف الزاوية وضعف الزاوية، على التوالي، بدءاً بقيمة معروفة، مثل sin(π/2) = 1.
تستخدم الحواسيب والحاسبات الحديثة مجموعةً متنوعةً من التقنياتِ لتوفير قيم الدوال المثلثية عند الطلب للزوايا الأخرى. تتمثل إحدى الطرق الشائعة، خاصةً في المعالِجات الراقية ذات وحدات الفاصلة العائمة، في جمع بين تقريب بواسطة كثير الحدود أو بواسطة الدوال الكسرية (مثل تقريب تشيبيشيف، تقريب بادي، وعادةً ما يتعلق بالدقة العليا أو المتغيرة، متسلسلات تايلور ومتسلسلة لوران) وتقليص المدى والبحث في الجدول—تبحث (الخوارزميات) أولاً في جدول صغير عن أقرب زاوية، ثم تستخدم كثير الحدود لحساب التصحيح.[46][47] على الأجهزة الأكثر بساطة التي تفتقر إلى مضاعف العتاد، توجد خوارزمية تسمى CORDIC عالية الكفاءة، لأنها تَستَخدِم الإزاحات والإضافة والطرح فقط.[عر 19]
يمكن تقريب الدوال المثلثية بواسطة المتوسط الحسابي الهندسي عندما يصبح تقارب المتسلسلة بطيئًا للغاية في الحسابات عالية الدقة، الذي يقارب في حد ذاته الدالة المثلثية بواسطة تكامل إهليلجي (مركب).[48]
متطابقات أساسية ومبرهنات[عدل]
هناك عدد من المتطابقات تربط الدوال المثلثية بعضها ببعض. يحتوي هذا القسم على المتطابقات الأساسية والمبرهنات، لمزيد من المتطابقات، طالع قائمة المتطابقات المثلثية. يمكن إثبات هذه المتطابقات هندسيا من التعريف باستعمال دائرة الوحدة أو التعريف باستعمال المثلث القائم (على الرغم من أنه بالنسبة للتعاريف الأخيرة، يجب توخي الحذر للزوايا التي لا تنتمي إلى هذا المجال [0 , π/2]). بالنسبة إلى البراهين غير الهندسية التي تستخدم فقط أدوات حساب التفاضل والتكامل، يمكننا استخدام المعادلات التفاضلية مباشرة. يمكننا أيضا استخدام متطابقة أويلر للتعبير عن جميع الدوال المثلثية بدلالة الدالة الأسية ذات القيم المركبة واستخدام خصائص الدالة الأسية.
متطابقة فيثاغورس[عدل]
تنص هذه المتطابقة على أن مجموع مربع جيب زاوية ما ومربع الجيب التمام لنفس الزاوية يساوي الواحد، ويُعبر عنها رياضياً بالعلاقة التالية:
يجب الانتباه إلى أن التدوين sin2 x + cos2 x يكافئ sin x)2 + (cos x)2).
متطابقات مجموع وفرق زاويتين[عدل]
تسمح صيغ الفرع والمجموع بتوسيع الجيب وجيب التمام والظل لمجموع أو فرق زاويتين بدلالة جيب وجيب تمام وظل الزوايا نفسها.
المجموع[عدل]
ويُحسب كما يأتي:

الفرق[عدل]
ويُحسب كما يأتي:

متطابقات ضعف الزاوية[عدل]
عندما تكون الزاويتان متساويتان، فإن صيغ المجموع تقلص إلى معادلات أبسط تعرف باسم متطابقات ضعف الزاوية.

يمكن استخدام هذه المتطابقات لاشتقاق متطابقات تحويل المجموع إلى الجداء.
بوضع θ = 2x وt = tan(x) هذا يسمح بالتعبير عن جميع الدوال المثلثية لـ θ كدالة كسرية لـ
بالإضافة إلى
هذا هو تعويض ظل نصف الزاوية، ويسمى أيضاً تعويض فايرشتراس، وهو يسمح بتقليص حساب التكاملات والمشتقات العكسية للدوال المثلثية إلى دوال كسرية.[وب 11]
متطابقات ثلاثية الزاوية[عدل]
ويُحسب كما يأتي:

متطابقات نصف الزاوية[عدل]
وتُحسب كما يأتي:[49]

قانون الجيب[عدل]
ليكن ABC مثلث، وa وb وc أضلاعه، ينص قانون الجيب على ما يلي:
- حيث تشير Δ إلى مساحة المثلث، أو بشكل مكافئ:
- حيث يشير R إلى نصف قطر الدائرة المحيطة بالمثلث.
يمكن إثبات ذلك بتقسيم المثلث إلى مثلثين قائمين وباستخدام التعريف الوارد أعلاه للجيب. قانون الجيب مفيد في حساب أطوال الأضلاع المجهولة في مثلث إذا كانت هناك زاويتان وضلع واحد معلومتان. هذا هو الموقف الشائع الذي يحدث في التثليث، وهي تقنية لتحديد مسافات غير معروفة عن طريق قياس زاويتين ومسافة مغلقة يمكن الوصول إليها.

في حالة المثلثات الكروية، ينص القانون على ما يلي:[15]
حيث a و b و c هي أقواس المثلث الواقع في سطح الكرة (والتي يطلق عليها مجازًا أضلاع وتسمى أحيانًا جوانب المثلث الكروي)؛ و A و B و C هي الزوايا المقابلة.[ملاحظة 12]
قانون جيب التمام[عدل]

قانون جيب التمام هو تعميم لمبرهنة فيثاغورس على أنواع المثلثات المستوية كلها، ويسمى أيضا مبرهنة الكاشي.[19]
وقد تكتب هذه الصيغة كما يلي:
- مع C هي الزاوية المقابلة للضلع c.
- يمكن إثبات هذه المبرهنة بتقسيم المثلث إلى مثلثين قائمين وباستخدام مبرهنة فيثاغورس، أو باستخدام طريقة الكاشي.
- يمكن استخدام قانون جيب التمام لحساب طول ضلع المثلث إذا كان الضلعان والزاوية بينهما معلومة. يمكن أيضًا استخدامه لإيجاد جيب تمام لأي زاوية إذا كانت أطوال كل الأضلاع معلومة.
في حالة المثلثات الكروية، ينص القانون على ما يلي:[50]
مع a وb وc هي الأقواس الثلاثة للمثلث الكروي وتقاس بالدرجات القوسية أي بقيمة الزاوية المركزية المقابلة لكل منها داخل الكرة، حيث تحول بعد ذلك إلى وحدات الطول العادية بالضرب في قيمة الدرجة القوسية والتي تساوي محيط الكرة360} ما يعادل ط × نصف قطر الكرة180 والرمز ط هنا أو π في اللاتينية؛ والزاوية C هي الزاوية المقابلة للقوس c
ويمكن اشتقاق المعادلة التالية مِن العلاقة السابقة لإيجاد قيمة الزاوية C المقابلة للقوس c في المثلث الكروي عندما تكون مجهولة وبقية الأطوال الثلاثة لأقواس المثلث a وb وc معلومة:
توجد صورة أخرى للمعادلة تكون قيم الزوايا الثلاثة فيها A وB وC معلومة وطول القوس مجهولٌ في المثلث الكُرويّ، وليكن القوس c، كما يلي:
ومنها يمكن حساب قيمة زاوية مجهولة بمعلومية طول القوس المقابل لها ومعلومية قيمتي الزاويتين الأخرتين بالمثلث الكروي هكذا:
قانون الظل[عدل]
ليكن ABC مثلث، يُكتب قانون الظل كما يلي:[51]

مع A وB وC الزوايا المقابلة للأضلاع a وb وc على الترتيب.
يمكن إثبات هذه المبرهنة باستخدام قانون الجيب والمتطابقات المثلثية.
أما بالنسبة للمثلثات الكروية، ينص القانون على ما يلي:[52]

قانون ظل التمام[عدل]
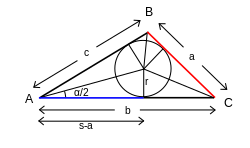

ليكن ABC مثلث، وa وb وc أضلاعه (حيث a=BC وb=AC وc=AB)، إذا كان:
- (نصف قطر الدائرة الداخلية للمثلث)
و
- (نصف محيط المثلث)،
ثم كل ما يلي يشكل قانون ظل التمام:[51]
نستنتج أن:
مبرهنة الساندويتش[عدل]
تساعد هذه المبرهنة في حساب النهايات الصعبة ومشتقات الدوال المثلثية. هذه المتباينة الصالحة فقط عند المجال ، هي كما يلي:
تمكننا هذه المتباينة من حساب النهاية التالية:[53] . تفيد هذه النهاية في حساب مشتقات الدوال المثلثية، طالع تفاضل الدوال المثلثية.
المتباينات المشابهة هي كما يلي:[54]

مبرهنة بطليموس[عدل]

مبرهنة بطليموس هي علاقة بين الأضلاع الأربعة وقطرا الرباعي الدائري (رباعي محاط بدائرة تشمل جميع رؤوسه).
ليكن ABCD رباعي دائري، إذا كان θ1+θ2+θ3+θ4=180°، فإن:[55]
صيغة مولفيده[عدل]
لتكن a و b و c أطوال أضلاع للمثلث، و α و β و γ الزوايا المقابلة لتلك الأضلاع الثلاثة على التوالي. تنص صيغة مولفيده على ما يلي:[56]

قانون موري[عدل]
ينص هذا القانون الرياضي على أن جداء جيوب التمام لكل من 20° و40° و80° يساوي 1/8، بتعبير رياضي:
- cos(20°).cos(40°).cos(80°) = 1/8
وهي حالة خاصة للمتطابقة العامة:
مع n=3 وα=20°.
هذه المتطابقة تثير الفضول، لأن، عند تعويض n و α للحد الثاني بتلك القيم، تكون النتيجة:
بما أن:
- sin(180°-x) = sin(x)
توجد متطابقة مشابهة لهذه المتطابقة، وهي متعلقة بدالة الجيب:
- sin(20°).sin(40°).sin(80°) = √3/8
زيادة على ذلك، عند تقسيم المتطابقة الثانية على الأولى، تنتج متطابقة أخرى:[57]
- tan(20°).tan(40°).tan(80°) = √3 = tan(60°)
الدوال العكسية[عدل]
الدوال المثلثية دورية، وبذلك، هي ليست متباينة، وبالتالي ليس لديها دالة عكسية. ومع ذلك، في كل مجال تكون فيه الدالة المثلثية رتيبة، يمكن للمرء تحديد دالة عكسية، بهذه الطريقة، تعرّف الدوال المثلثية العكسية كدوال متعددة القيم. لتعريف دالة عكسية حقيقية، يصير من الضروري تقليص مجال تعريفها إلى مجال تكون فيه الدالة رتيبة، حتى تكون الدوال المثلثية دوالا تقابلية. يعطى الاختيار الشائع لهذا المجال الذي يطلق عليه اسم «مجموعة القيم الرئيسية» في الجدول التالي. عادة ما يشار إلى الدوال المثلثية العكسية بالبادئة "arc" قبل اسم الدالة أو اختصارها.
يوضح الجدول الآتي قائمة الدوال المثلثية العكسية مع إبراز المنطلقات والمستقرات والمشتقات.[عر 20]
غالبًا ما تستخدم التدوينات sin−1 وcos−1... إلخ للتعبير عن arcsin وarccos ،... وهكذا. عند استخدام هذا التدوين، قد يؤدي هذا إلى الالتباس بين الدوال العكسية والمعاكيس الضربية.
يمنع التدوين بالبادئة "arc" مثل هذا الالتباس، على الرغم من أنه يمكن الخلط بين "arcsec" لـ arcsecant و لـ "arcsecond"(التي تعني «ثانية القوس»).
يُمكن للدوال المثلثية العكسية أن تعرف بواسطة المتسلسلات تماما كما هو الحال بالنسبة للدوال المثلثية. على سبيل المثال،
يمكن أيضًا التعبير عنها بدلالة اللوغاريتمات المركبة.[وب 12]
الدوال الزائدية[عدل]

الدوال الزائدية هي تلك الدوال التي تشبه الدوال المثلثية لكنها معرفة بواسطة القطع الزائد بدلاً من الدائرة: تمامًا كما تشكل النقاط (cos(t), sin(t)) دائرة ذات نصف قطر يساوي الواحد، تشكل النقاط (cosh(t), sinh(t)) النصف الأيمن للقطع الزائد.
الدوال الزائدية هي:
يعتمد كلا النوعين على عُمدة، إما زاوية دائرية أو زاوية زائدية.
بما أن مساحة القطاع الدائري الذي نصف قطره r وزاويته u هي ، فسوف تكون مساوية لـ u عندما تكون r=√2. في الرسم البياني، تكون الدائرة مماسية على القطع الزائد الذي معادلته xy = 1 عند النقطة (1,1). يمثل القطاع البرتقالي مساحة ومقدار الزاوية الدائرية. وبالمثل، تمثل القطاعان الأصفر والأحمر معًا مساحة ومقدار الزاوية الزائدية.
سيقان المثلثين القائمين اللذين وتراهما هما عبارة عن شعاع محدد للزوايا يبلغ طولهما 2√ مرة الدوال الدائرية والزائدية.
في حالة القطع الزائد الذي معادلته x2 - y2 =1، مقدار الزاوية الزائدية هو ضعف المساحة الزرقاء المحددة بنصف المستقيم ومحور السينات والقطع الزائد، تماما كما يكون مقدار الزاوية الدائرية هو ضعف المساحة الزرقاء للدائرة التي معادلتها: x2 + y2 =1.
في المتطابقات الزائدية، هناك تشابه كبير بينها وبين المتطابقات المثلثية، بعض الأمثلة على ذلك:

هناك علاقة تربط الدوال المثلثية بالدوال الزائدية دون اللجوء إلى استخدام الأعداد المركبة تُعْرَف بالدالة الغودرمانية، وهي معرّفة في ℝ نحو بـ:[58][59][وب 13]
وsgn (x) هي دالة الإشارة.
-
(4.ب) الدائرة والقطع الزائد متلامسان عند النقطة (1,1) تعرضان هندسة الدوال الدائرية بدلالة مقدار الزاوية u، والدوال الزائدية اعتمادًا على مقدار الزاوية u.
-
(4.ج)
-
(4.د)
علاقة الدوال المثلثية بالدوال الخاصة[عدل]
يمكن كتابة بعض الدوال الخاصة بدلالة مجموعة من الدوال بما في ذلك الدوال المثلثية.
- دالة بيسل من المرتبة 1/2: دالة بيسل التي هي عبارة عن متسلسلة القوى، هي حل للمعادلة التفاضلية من الدرجة الثانية التالية:
حيث يمثل a المرتبة. يمكن كتابة أحد الحالات الخاصة لدالة بيسل (a = 1/2) بدلالة الدوال المثلثية على النحو التالي:[60]
- متعدد الحدود لتشيبيشيف: هو الحل للمعادلة التفاضلية من الدرجة الثانية التالية:
مع n ممثلةً للمرتبة.
يمكن كتابة متعدد الحدود لتشيبيشيف من المرتبة n بدلالة الدوال المثلثية:[61]
Tn = cos(n.arccos(x))
تطبيقات[عدل]
حساب المتجهات[عدل]
تُستخدم المتجهات (التي لها مقدار واتجاه) لتمثيل كمية متجهة في الرياضيات والفيزياء مثل تمثيل القوة والسرعة. تستخدم بعض حسابات المتجهات دوال مثلثية. على سبيل المثال، يمكن حساب الضرب النقطي لمتجهين x وy بواسطة قانون جيب التمام:
يمكن أيضًا استخدام المعادلة التالية لحساب مقدار الضرب المتجهي:
الإحداثيات القطبية، والأسطوانية والكروية[عدل]

الدوال المثلثية هي الأساس لتحديد نظام الإحداثيات القطبية الذي يكون فعالا في تبسيط العديد من المشكلات الرياضية والفيزيائية، بما في ذلك بعض التكاملات. في نظام الإحداثيات هذا، بدلاً من إحداثيات x وy لنقطة (المستخدمة في نظام الإحداثيات الديكارتية)، بُعدها عن المركز والزاوية المحصورة بين الخط الذي يربطها بالمركز والخط الأفقي (r , θ) فهي تعتبر إحداثيات النقطة. تحويل الإحداثيات الديكارتية إلى الإحداثيات القطبية والعكس بالعكس باستخدام الدوال المثلثية:
- x = r cos(θ), y = r sin(θ)
تتشكل أيضًا أنظمة الإحداثيات الأسطوانية والكروية، التي تعد إحداثيات قطبية معممة على ثلاثية الأبعاد، على أساس الدوال المثلثية. تُستخدم هذه الأنظمة في مشكلات مثل تكاملات ثلاثية الأبعاد لها تناظر أسطواني أو كروي.
المساحات[عدل]
- مثلث: هناك قانون يعبر عن مساحة المثلث بدلالة أضلاعه a وb والزاوية المحصورة بينهم θ دون الحاجة إلى معرفة ارتفاعه:[عر 21]
- (S = (1/2).ab.sin(θ
- متوازي أضلاع: يمكن ايجاد مساحته من خلال معرفة أطوال أضلاعه a وb وإحدى زواياه θ دون الحاجة إلى معرفة ارتفاعه بتطبيق هذا القانون:[وب 14]
- (S = ab.sin(θ
- مضلع منتظم: يمكن ايجاد مساحته من خلال تلك الصيغ:[62]
- مع n عدد الأضلاع وl هو طول أحد الأضلاع وp هو محيط المضلع.
- إذا كان المضلع محاط بدائرة نصف قطرها R ومحيط بدائرة نصف قطرها r (يُغدُّ أيضًا عامد المضلع):
المحيطات[عدل]
- مضلع منتظم: يمكن إيجاد محيطه بدلالة عدد أضلاعه n والمسافة بين مركز المضلع وأحد رؤوسه b ودالة الجيب:[63]
- 2nb.sin(π/2)
- قطع ناقص: يمكن إيجاد محيطه إنطلاقًا من نصف محوره الأكبر a والأصغر b باستخدام إحدى الدوال المثلثية:[64]
- مع هو معامل التباعد المركزي، وE هو التكامل الإهليلجي التام من النوع الثاني:
- يتم الحصول على هذا القانون باستخدام صيغة حساب طول القوس والإحداثيات القطبية.[ملاحظة 14]
الحجوم[عدل]
- متوازي السطوح: يمكن تعبير عن حجمه بدلالة جيب التمام:
مع وa,b,c هي أطوال الأحرف.
علاقتها بالدالة الأسية وبالأعداد المركبة[عدل]

- يمكن كتابة أي عدد مركب على الشكل المثلثي:
- z = |z| (cosθ + isinθ) و|z| هو القيمة المطلقة للعدد المركب، وi هي وحدة تخيلية مربعها يساوي واحد.
يطلق على العلاقة بين الدالة الأسية والدوال المثلثية اسم صيغة أويلر:
إثبات:[65] لتكن متسلسلة تايلور للدالة الأسية:
بوضع: x=iθ، تصبح المتسلسلة:
من متسلسلتا ماكلورين لدالتي الجيب وجيب التمام:
فيُبصح:
قد تستعمل صيغة أويلر للحصول على بعض المتطابقات المثلثية، وذلك بكتابة دالتي الجيب والجيب التمام كما يلي:
- يمكن ملاحظة أن جيب التمام يمكن اعتباره الجزء الحقيقي والجيب هو الجزء التخيلي للدالة الأسية المركبة. رياضيا:
- يعرف الشكل المعمم لصيغة أويلر باستعمال صيغة دي موافر:
- أيضًا، باستخدام تعريف بواسطة متسلسلة ماكلورين للدوال الزائدية والمثلثية، يمكن الحصول على العلاقات بين تلك الدوال:
علم الفلك[عدل]
استخدمت حساب المثلثات الكروية لعدة قرون لتحديد موقع الشمس والاقمار والنجوم، والتنبؤ بالكسوف والخسوف، ووصف مدارات الكواكب.
في العصر الحديث، تستخدم تقنية التثليث في علم الفلك لقياس مسافة النجوم القريبة، وكذلك في أنظمة الملاحة عبر الأقمار الصناعية.[66]
الخرائط والمساحة[عدل]

حساب المثلثات هو أساس معظم ممارسات رسم الخرائط والمساحة. قياس زاوية باستخدام الجهاز أو دون استخدامه، إسقاط الخرائط (تحويل سطح ناقصي إلى سطح مستوي)، وتحديد الارتفاعات، وحساب الاتجاه الزاوي، والمسح الاجتيازي المفتوح والمغلق،[ملاحظة 15] وتصميم الأقواس في إنشاء الطرقات، وتحويل ثنائي الأبعاد في المسح الجوي.
على سبيل المثال، في التثليث، وهي إحدى الطرق القديمة للمساحة، نحسب احداثيات نقطة معينة من خلال قياس الزوايا بين نقطتين مرجعيتين؛ يُستخدم هذا المبدأ حاليًا في القياس البصري الثلاثي الأبعاد [الإنجليزية]. يُستخدَم في التثليث قانون جيب التمام وقانون الجيب لحساب زوايا المثلثات وتحديد الموقع الدقيق لكل نقطة.
في الحالة المبينة في الشكل (5.ج)، تُحسَب المسافة بتطبيق هذا القانون:

قياس ارتفاع جبل أو مبنى مرتفع، ليكن h، هو مثال آخر عن التثليث، وعندها تُحدد الزوايا α و β من نقطتين أرضيتين إلى الأعلى (الشكل (5.د)). لتكن ℓ مسافة بين هذه النقاط، يحسب الارتفاع بتطبيق هذا القانون:
متسلسلة فورييه وتحويل فورييه[عدل]
دالتا الجيب وجيب التمام مثل كثيرات الحدود المتعامدة مستقلةٌ خطياً. ومنهم يمكن كتابة أي دالة (دورية بشكل عام) على أنها العلاقة التالية بدلالة متسلسلة من تلك الدوال، والتي تسمى متسلسلة فورييه:
بالنسبة للدوال الفردية، فقط حدود دالة الجيب، أما الدوال الزوجية، فقط حدود دالة جيب التمام زائد معامل ثابت.
تحويل فورييه هو نوع من التحويل التكاملي وهو عبارة عن امتداد لمتسلسلة فورييه. يُعرف هذا التحويل بـ:[وب 15]
تُحوّل الدالة الأسية المركبة إلى دوال مثلثية بواسطة صيغة أويلر. تستخدم تحويل فورييه لحل المعادلات التفاضلية الجزئية مثل معادلة الموجة والتحليل الطيفي ومعالجة الإشارات.[67]
يستخدم تحويل جيب التمام المتقطع القريب من تحويل فورييه لتقليل حجم ملف JPEG في أثناء التخزين مع الحفاظ على الجودة النسبية (ضغط الصور)، هذا التحويل هو تقنية تمثل البيانات على شكل مجاميع دوال جيب التمام.[68]
الدوال الدورية[عدل]

الدوال المثلثية مهمة أيضا في الفيزياء. على سبيل المثال، يُستخدام الجيب وجيب التمام لوصف الحركة التوافقية البسيطة، التي تنمذج العديد من الظواهر الطبيعية، مثل حركة كتلة متصلة بنابض (نواس مرن [الإنجليزية])، وبالنسبة للزوايا الصغيرة، حركة كتلة معلقة بواسطة خيط (نواس بسيط)؛[69] وفي الكهرباء والإلكترونيات، تستخدم الدالتان الأخيرتان لدراسة الدارات الكهربائية مثل دارة مقاومة وملف ومكثف المهتزة. دوال الجيب وجيب التمام هي اسقاطات أحادية البعد لحركة دائرية منتظمة.[70]
تثبت الدوال المثلثية أيضًا على أنها مفيدة في دراسة الدوال الدورية العامة. تُعد أنماط الموجات المميزة للدوال الدورية مفيدة لنمذجة الظواهر المتكررة مثل الصوت أو الموجات الضوئية.
يمكن عموماً التعبير عن دالة دورية f(x) بصفتها مجموع موجات الجيب أو موجات جيب التمام في متسلسلات فورييه مثل موجة مربعة أو موجة سن المنشار.[67]
نشير إلى الدالة التي تتضمن الجيب أو جيب التمام بـ φk، يأخذ مفكوك الدالة الدورية f(t) الشكل:
حيث ck هو معامل المتسلسلة.
على سبيل المثال، يمكن كتابة الموجة المربعية كمتسلسلة فورييه:
في الصورة المتحركة لموجة مربعية (5.هـ)، يمكن ملاحظة أن بعض الحدود فقط تنتج تقريبًا جيدًا إلى حد ما.
المنحنيات الوسيطية[عدل]

يمكن تمثيل بعض المنحنيات الخاصة باستخدام المعادلات الوسيطية وبدلالة الدوال المثلثية، بعض من الأمثلة على المنحنيات الخاصة هي كما يلي:
- الدائرة: تعطى المعادلة الوسيطية للدائرة ذات المركز ونصف القطر r بواسطة:
-
- القطع الناقص: يُمثَّل القطع الناقص ذو المركز ونصف المحور الكبير a ونصف المحور الصغير b كما يلي:
- منحنى ليساجو: يُعبَّر عن منحنى ليساجو بواسطة:[وب 16]
- مع و هي عبارة عن ثوابت تصف عدد فصوص الشكل.
- القطع الزائد، يمكن تمثيل وسيطيًا القطع الزائد الأفقي بواسطة:
- أو
- ويمكن تمثيل القطع الزائد العمودي وسيطيًا كما يأتي:
- أو
- مع (h , k) هي مركز القطع الزائد.
بالإضافة إلى تلك المنحنيات، يمكن أيضًا تمثيل عدة رسومات التي تعتمد على الدوال المثلثية، بما في ذلك المنحنى العجلي التحتي، اللولب، السطوح الوسيطية [الإنجليزية]،... وهكذا.
البصريات[عدل]

التطبيق الأساسي للدوال المثلثية في علم البصريات هو قانون سنيل. ينص هذا القانون، الذي ينطبق على ظاهرة انكسار الضوء، على العلاقة بين زوايا السقوط والانكسار:
حيث:
- θ1: زاوية سقوط الموجة، θ2: زاوية انكسار الموجة.
- v1: سرعة الضوء في الوسط الأول، v2: سرعة الضوء في الوسط الثاني.
- n1: معامل الانكسار للوسط الأول، n2: معامل الانكسار للوسط الثاني
بالإضافة إلى انكسار الضوء، تُستخدم الدوال المثلثية في مجالات أخرى من البصريات، مثل تحليل تداخل الموجات والاستقطاب والحيود.
الملاحة[عدل]

تاريخيا، استخدمت حساب المثلثات لتحديد احداثيات خطوط الطول والعرض لسفن الإبحار، ورسم المسارات، وحساب المسافات في أثناء الملاحة.
لا يزال حساب المثلثات مستخدمًا في الملاحة من خلال وسائل مثل نظام التموضع العالمي (GPS) والذكاء الاصطناعي للمركبات الذاتية.[29]
تُستخدم هذه المعادلة لتحديد المسافة بين نقطتين على الأرض:[ملاحظة 16]
مع:
يمكن إثبات ذلك من قانون جيب التمام للمثلثات الكروية.[71]
الفيزياء الميكانيكية[عدل]
في الفيزياء الميكانيكية، تُطبق الدوال المثلثية على معادلات الحركة ثنائية الأبعاد وثلاثية الأبعاد، وحتى في دراسة حركة الأجسام. على سبيل المثال، عند تحليل الاختلافات الدورية في الحركيات والديناميكيات الدورانية، ومعادلات الزخم والزخم الزاوي، وظواهر التصادم، نستخدم فيها دوال مثلثية.
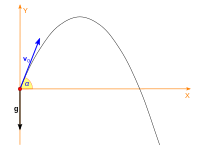
من أكثر التطبيقات المعروفة للدوال المثلثية في الميكانيكا هي دراسة ظاهرة حركة جسم مقذوف بزاوية α، وتكتب المعادلة الوسيطية لمسارها بدلالة الزمن t على النحو التالي:
مع x وy إحداثيات موضع الجسم عند الثانية t والسرعة الإبتدائية هي v0 وg هي قوة التسارع.
أيضا، تُحسب سرعة الجسمين V1 وV2 ومقدار الزاويتين θ وφ اللتين صنعهما الجسمان بعد التصادم المرن باستخدام الدوال المثلثية، بتطبيق قانون حفظ الزخم (في كلا المعادلتين، قبل تصادم جسمين (على اليسار) = بعد تصادم جسمين (على اليمين)):
ثابت : على المحور x
ثابت : على المحور y
القبلة[عدل]

القبلة هي وجهة المصلي عند الصلاة وهي عند المسلمين الكعبة المشرفة في مدينة مكة.
يتم تطبيق نموذج الدائرة العظمى لحساب القبلة باستخدام حساب المثلثات الكروية، وهو العلم الذي برع فيه العلماء المسلمين قديمًا واستقر العمل في تحديد القبلة عليه. في الشكل التالي، يشكل موقع المصلي O والكعبة Q والقطب الشمالي N مثلثًا على الكرة الأرضية. يُشار إلى القبلة بـ OQ، وهي اتجاه الدائرة العظمى التي تشمل النقطتين O و Q. يمكن أيضًا التعبير عن القبلة كالزاوية ∠NOQ (أو ∠q للقبلة بالنسبة للشمال، وتسمى أيضًا «إنحراف القبلة». يمكن حساب هذه الزاوية كدالة رياضية لخط عرض موقع المصلي Φ، وخط عرض الكعبة ΦQ، والفرق بين خطي طول الموقعين المذكورين سابقًا ΔL،[72] هذه الدالة مستمدة من قاعدة ظل التمام التي تنطبق على أي مثلث كروي ذات الزوايا A وB وC والجوانب a وb وc:
بتطبيق هذه الصيغة على المثلث الكروي NOQ (بتعويض B = ∠q = ∠NOQ) وبتطبيق المتطابقات المثلثية، يكون:
، ومنه يكون:[72]
الهندسة الكهربائية والاتصالات[عدل]

تستخدم التيارات المتناوبة في تزويد المنازل والمصانع بالطاقة الكهربائية، ويُعبَّر عنها بشكل موجة جيبية. أحد الأسباب الرئيسية لتفضيل التيار المتناوب على التيار المستمر في الصناعة هو إمكانية تحويل مستوى الجهد للتيار المتناوب باستخدام المحولات، وهذا يُقلل من الطاقة الضائعة عند النقل لمسافات طويلة ويجعلها ذات ربح عالٍ، بالإضافة لإمكانية عدم استعمال المبادلات في المولدات.
تولد محطات الكهرباء تيارات ثلاثية الطور في الغالب. يمكن وصف تغير التيار المتناوب بتلك المعادلات: و [ملاحظة 17] وبالتالي تُحسب وتُحدد علاقات مختلفة مثل القدرة اللحظية، القدرة الفعالة، القدرة غير الفعالة،[ملاحظة 18] … إلخ، أو مفاهيم مثل تقدم الطور، وتأخر الطور وزاوية القدرة ومعامل القدرة، …، من خلال تحليل الدوال المثلثية.[وب 17] الكهرباء التي تُغذى بها المنازل هي موجة جيبية ترددها غالباً ما يكون 50 أو 60 هرتز.
تُنمذج محددات خط نقل الطاقة الكهربائية باستعمال دوال زائدية.
في أنظمة الاتصالات، عادة ما تدعم كل قناة الاتصال نقل إشاراتٍ فقط في نطاق ترددي معين، ويتعذر إرسال الإشارة عبر القناة إذا كان ترددها خارج هذا النطاق. ولذلك، من أجل إرسال إشارة لها تردد خارج النطاق، عادة ما يتم تثبيتها على موجة أخرى لها تردد متوافق مع نطاق القناة، تُسمَّى هذه التقنية التضمين. في الإشارات التماثلية تكون الموجة الحاملة موجة جيبية. على سبيل المثال، في تضمين السعة، تُضرب الإشارة التي تحتوي على المعلومات في الموجة الحاملة للموجة الجيبية.[73]
ملحق: مسرد المصطلحات الإنجليزية[عدل]
| مَسرد المفردات وفق الترتيب الأبجدي الإنجليزي | |
| A | |
| إحداثي x/إحداثي سيني | Abscissa |
| قيمة مطلقة لعدد مركب | Absolute value of complex number |
| زاوية حادة | Acute angle |
| ضلع مجاور | Adjacent side |
| عدد جبري | Algebraic number |
| زاوية | Angle |
| متطابقات مجموع وفرق زاويتين | Angle sum and difference identities |
| مشتق عكسي | Antiderivative |
| تقريب | Approximation |
| قوس | Arc |
| مساحة | Area |
| عُمدة | Argument |
| متوسط حسابي هندسي | Arithmetic–geometric mean |
| B | |
| عدد بيرنولي | Bernoulli number |
| دالة بيسل | Bessel function |
| دالة تقابلية | Bijective function |
| C | |
| حساب التفاضل والتكامل | Calculus |
| معادلة مميزة | Characteristic equation |
| تقريب تشيبيشيف | Chebyshev approximation |
| متعدد الحدود لتشيبيشيف | Chebyshev polynomial |
| دالة الوتر | Chord |
| زاوية دائرية | Circular angle |
| حركة دائرية | Circular motion |
| قطاع دائري | Circular sector |
| محيط دائرة/قطع ناقص (منحنى مغلق بشكل عام) | Circumference |
| مضلع محيط | Circumscribed polygon |
| مستقر دالة | Codomain of a function |
| فرجار | Compass |
| زوايا متتامة | Complementary angles |
| تحليل مركب | Complex analysis |
| عدد مركب | Complex number |
| مستوي مركب | Complex plane |
| دالة مستمرة/دالة متصلة | Continuous function |
| إحداثيات | Coordinates |
| لازمة | Corollary |
| ضرب متجهي /جداء متجهي | Cross product |
| جذر تكعيبي | Cube root |
| سهم التمام | Coversine |
| رباعي دائري | Cyclic quadrilateral |
| إحداثيات أسطوانية | Cylindrical coordinates |
| D | |
| صيغة دي موافر | De Moivre's formula |
| درجة | Degree |
| مقام | Denominator |
| مشتق | Derivative |
| قطر الدائرة | Diameter |
| فرق | Difference |
| تفاضل | Differential |
| معادلة تفاضلية | Differential equation |
| متطابقات ضعف الزاوية | Double-angle identities |
| مجال دالة | Domain of a function |
| ضرب نقطي/ضرب قياسي/جداء سلمي | Dot product |
| E | |
| تباعد مركزي | Eccentricity |
| أحرف متعدد السطوح | Edges of a polyhedron |
| دالة ذاتية | Eigenfunction |
| قطع ناقص | Ellipse |
| تكامل إهليلجي/ناقصي | Elliptic integral |
| دالة صحيحة | Entire function |
| مثلث متساوي الأضلاع | Equilateral triangle |
| متطابقة أويلر | Euler's identity |
| عدد أويلر | Euler number |
| دوال زوجية وفردية | Even and odd functions |
| قاطع التمام الخارجي | Excosecant |
| قاطع خارجي | Exsecant |
| دالة أسية | Exponential function |
| F | |
| عاملي عدد | Factorial of a number |
| وحدة الفاصلة العائمة | Floating Point Unit |
| متسلسلة فورييه | Fourier series |
| تحويل فورييه | Fourier transform |
| G | |
| نظرية غالوا | Galois theory |
| كسر مستمر معمم | Generalized continued fraction |
| تشابه هندسي | Geometric similarity |
| تمثيل بياني لدالة | Graph of a function |
| H | |
| متطابقات نصف الزاوية | Half-angle identities |
| نصف السهم | Haversine |
| لولب | Helix |
| المعالِجات الراقية | Higher-end Processors |
| دالة تامة التشكل | Holomorphic function |
| قطع زائد | Hyperbola |
| زاوية زائدية | Hyperbolic angle |
| دوال زائدية | Hyperbolic functions |
| قطاع زائدي | Hyperbolic sector |
| وتر المثلث | Hypotenuse |
| منحنى عجلي تحتي | Hypotrochoid |
| I | |
| وحدة تخيلية | Imaginary unit |
| متباينة | Inequality |
| دالة متباينة | Injective function |
| مضلع محاط | Inscribed polygon |
| تكامل | Integral |
| عدد صحيح | Integer number |
| مجال/فترة | Interval |
| تقاطع مستقيمين | Intersection of two lines |
| متسلسلة الجداء اللانهائي | Infinite product expansion |
| دالة عكسية | Inverse function |
| نقطة معزولة | Isolated point |
| L | |
| تحويل لابلاس | Laplace transform |
| مؤثر لابلاسي | Laplace operator / Laplacian |
| قانون جيب التمام | Law of cosines |
| قانون الجيب | Law of sines |
| ساق مثلث | Leg of a triangle |
| طول | Length |
| نهاية دالة | Limit of a function |
| مستقيم | Line |
| منحنى ليساجو | Lissajous curve |
| M | |
| متسلسلة ماكلورين | Maclaurin series |
| مقدار | Magnitude |
| دالة جزئية التشكل | Meromorphic function |
| ميليراديان | Milliradian |
| تضمين | Modulation |
| صيغة مولفيده | Mollweide's formula |
| دالة رتيبة | Monotonic function |
| قانون موري | Morrie's law |
| دالة متعددة القيم | Multivalued function |
| N | |
| مقابل عدد | Negative of a number |
| بسط | Numerator |
| جذر نوني | nth root |
| O | |
| ضلع مقابل | Opposite side |
| إحداثي y/إحداثي صادي | Ordinate |
| نقطة الأصل | Origin |
| دوال متعامدة | Orthogonal functions |
| P | |
| تقريب بادي | Padé approximant |
| متوازي السطوح | Parallelepiped |
| متوازي أضلاع | Parallelogram |
| معادلة وسيطية | Parametric equation |
| جسم / جسيم | Particle |
| حركة رقاصية/حركة بندولية | Pendular motion |
| محيط (مضلعات) | Perimeter |
| دور | Period |
| دالة دورية | Periodic function |
| دورية | Periodicity |
| طور | Phase |
| تقدم وتأخر الطور | Phase leading and lagging |
| إحداثيات قطبية | Polar coordinates |
| متسلسلة قوى | Power series / Power expansion |
| مبرهنة بطليموس | Ptolemy's theorem |
| متطابقة فيثاغورس | Pythagorean identity |
| مبرهنة فيثاغورس | Pythagorean theorem |
| Q | |
| ربع الدائرة | Quadrant |
| قاعدة ناتج القسمة | Quotient rule |
| R | |
| نسبة | Ratio |
| نصف القطر | Radius |
| نصف قطر التقارب | Radius of convergence |
| تقليص المدى | Range reduction |
| سرعة التقارب | Rate of convergence |
| دالة كسرية | Rational function |
| عدد كسري/نسبي/ناطق/جذري | Rational number |
| عدد حقيقي | Real number |
| علاقة استدعاء ذاتي | Recurrence relation |
| خماسي منتظم | Regular pentagon |
| باقي (متسلسلة) | Remainder term |
| زاوية قائمة | Right angle |
| مثلث قائم الزاوية | Right-angled triangle / Right triangle |
| جذر معادلة/جذر دالة | Root |
| دوران | Rotation |
| S | |
| عمق القوس | Sagitta |
| نصف المحور الأكبر | Semi-major axis |
| نصف المحور الأصغر | Semi-minor axis |
| مجموعة القيم الرئيسة | Set of principal values |
| دالة الإشارة | Sign function |
| حركة توافقية بسيطة | Simple Harmonic Motion |
| موجة جيبية | Sine wave |
| قانون سنيل | Snell's law |
| حل المثلثات | Solution of triangles |
| زوايا خاصة | Special angles |
| دوال خاصة | Special functions |
| إحداثيات كروية | Spherical coordinates |
| مثلث كروي | Spherical triangle |
| حساب المثلثات الكروية | Spherical trigonometry |
| جذر تربيعي | Square root |
| موجة مربعية | Square wave |
| مبرهنة الساندويتش | Squeeze theorem / Sandwich theorem |
| مسطرة | Straightedge |
| طرح | Subtraction |
| مجموع | Sum |
| تناظر | Symmetry |
| T | |
| مماس | Tangent |
| تعويض ظل نصف الزاوية | Tangent half-angle substitution |
| متسلسلة تايلور | Taylor series |
| حدود | Terms |
| مبرهنة طاليس | Thales theorem |
| عدد متسامي | Transcendental numbers |
| مسح اجتيازي | Traverse |
| تثليث | Triangulation |
| علم المثلثات/حساب المثلثات | Trigonometry |
| متطابقات ثلاثية الزاوية | Triple-angle identities |
| دورة (وحدة قياس الزوايا) | Turn |
| U | |
| دائرة الوحدة | Unit circle |
| V | |
| متجه | Vector |
| سهم/ جيب معكوس | Versine |
| W | |
| تعويض فايرشتراس | Weierstrass substitution |
| X | |
| محور السينات | x-axis |
| Y | |
| محور الصادات | y-axis |
انظر أيضًا[عدل]
| في كومنز صور وملفات عن: دوال مثلثية |
هوامش وملاحظات[عدل]
- 101. نسبت مصادر مختلفة الاستخدام الاول للمصطلح "sinus" إلى:[1][4]
- إما ترجمة أفلاطون تيبورتينوس في عام 1116 لأعمال البتاني الخاصة بعلم الفلك.
- أو ترجمة جيراردو الكريموني لجبر الخوارزمي
- أو ترجمة روبرت أوف تشستر سنة 1145 لجداول الخوارزمي
- طالع: وMaor (1998), chapter 3, for an earlier etymology crediting Gerard.
- 102. جاء في كشاف اصطلاحات الفنون والعلوم للتهانوي: "الجيب: بالفتح وسكون المثناة التحتانية في اللّغة گريبان كما في الصّراح. وعند المهندسين والمنجمين هو نصف وتر ضعف القوس. [...] وهذا الذي ذكر هو الجيب المستوي. وما وقع من القطر بين جيب القوس وطرف القوس هو الجيب المعكوس ويسمّى بسهم القوس أيضا."[عر 7]
- 103. تنسب بعضٌ من المصادر الجدول الأول الموضوع للظل إلى حبش الحاسب[وب 18]
- ^ k هي عدد صحيح كيفي.
- ^ أو تلك التدوينات: cotan, cotg ctg, ctn
- ^ أو هذا التدوين: cosec
- ^ كانت العلاقة المثلثية لدالة الظل معروفة عند الهنود، ولكن لم يعتبروها كميةً مثلثيةً مستقلة كدالة الجيب.
- ^ أ ب يعني الشريط الأفقي فوق الرقم أنه يتكرر إلى ما لا نهاية.
- ^ يسمى أيضًا محور الفواصل أو محور الأفاصيل
- ^ عكس اتجاه عقارب الساعة لأجلِ زاويةٍ موجبةٍ θ > 0، وفي اتجاه عقارب الساعة من أجل زاويةٍ سالبةٍ θ < 0.
- ^ يسمى أيضا "عدد مركب"
- ^ نصف قطر التقارب لمتسلسلة قوى هو نصف قطر أكبر قرص تتقارب فيه المتسلسلة. وهو إما عدد حقيقي غير سالب وإما ∞.
- ^ حيث: a هو ثابت حقيقي. s هو عدد مركب.
- ^ مع: ω هي التردد الزاوي و(.)δ هي دالة ديراك وi هي وحدة تخيلية مربعها يساوي 1-.
- ^ أطوال الأضلاع تساوي عدديًا قياس الزوايا التي تقابل أقواس الدائرة العظمى في المركز بالراديان. لذلك، بالنسبة لكرة ذات نصف قطر R لا يساوي الواحد، يجب قسمة أطوال الأقواس على R قبل استخدام المتطابقة.
- ^ a=CB، و b=CA، و c=AB
- ^ تحسب القيمة فقط باستعمال الحاسبة أو باستعمال الحاسوب لأن التكاملات الإهليلجية لا يمكن التعبير عنها باستخدام الدوال الابتدائية مثل الدوال الجبرية والمثلثية والأسية واللوغاريتمية.
- ^ المسح الاجتيازي هو طريقة لمسح منطقة مفتوحة أو مغلقة باستخدام قياس الزوايا والمسافات.
- ^ يجب تحويل الإحداثيات إلى الراديان في الحساب.
- ^ حيث:
- i هي دالة التيار الكهربائي
- v هي دالة الجهد الكهربائي
- Vm وIm هما سِعَتا دالتي الجهد والتيار الكهربائيين على الترتيب.
- ω هو التردد الزاوي.
- θ هو الطور الابتدائي.
- ^ تسمى القدرة أيضًا الاستطاعة
مراجع[عدل]
فهرس المراجع[عدل]
- المنشورات
- بالعربية
- ^ مكتب التنسيق (1990)، ص. 153.
- ^ أ ب ت ث ج موير (2004)، ص. 22.
- ^ القوصي (2013)، ص. 88.
- ^ أ ب البعلبكي (2008)، ص. 1255.
- ^ أ ب ساسين (2007)، ص. 862.
- ^ دعبول (2018)، ص. 727.
- ^ أ ب التهانوي، ج. 1، ص. 605.
- ^ التهانوي، ج. 2، ص. 1150-1151.
- ^ أ ب دعبول (2018)، ص. 647 ،142 ،699 ،143 ،622 ،141.
- ^ مجمع القاهرة (1955)، ص. 292.
- ^ الأحمد (2004)، ص. 166.
- ^ الكلنبوي (2019)، ص. 151.
- ^ البيروني (2002)، ج. 1، ص. 275.
- ^ أ ب راشد (2005)، ج. 2، ص. 642-647.
- ^ الفيروزأبادي (1998)، ص. 1298.
- ^ البيروني (2002)، ج. 1، ص. 225.
- ^ الجيوسي (2005)، ص. 129.
- ^ موير (2004)، ص. 68.
- ^ محمود (2011)، ص. 53.
- ^ موير (2004)، ص. 123-126.
- ^ موير (2004)، ص. 199.
- بالإنكليزية
- ^ أ ب Katz (2009), p. 210.
- ^ Fogiel (1984), p. 211.
- ^ أ ب ت ث ج ح خ Plofker (2009), p. 257.
- ^ أ ب Merlet (2004), p. 196.
- ^ Simpson (1989), vol. 17, p. 608.
- ^ أ ب Rashid (1996), vol. 2, p. 505، 512.
- ^ Simpson (1989), vol. 14, p. 822.
- ^ Roegel (2010), p. 4.
- ^ Datta (1983), p. 40.
- ^ Krantz (2010), p. 81.
- ^ Eves (1983), p. 96.
- ^ أ ب ت ث ج Boyer (1991), p. 210.
- ^ Walker (1999), p. 167-168.
- ^ Gingerich (1983), p. 74.
- ^ أ ب ت ث Sesiano (2000), p. 157.
- ^ Rashid (1996), vol. 3, p. 769.
- ^ أ ب Tonias (2016), p. 16.
- ^ أ ب ت Guergour (2005), p. 420.
- ^ أ ب Pickover (2009), p. 106.
- ^ Anderson (2004), p. 139.
- ^ Imhausen (2007), p. 308.
- ^ Bradley (2007), p. 100.
- ^ Nielsen (1966), p. xxiii–xxiv.
- ^ Air Force (1954), p. 33.
- ^ Lindeburg (2012), p. 78-7.
- ^ Berresford (2015), p. 553.
- ^ أ ب ت ث Protter (1970), p. APP-2,APP-3.
- ^ Heng (2001), p. 228.
- ^ أ ب Larson (2013), p. 153.
- ^ Schaumberger (1974), p. 73-76.
- ^ Niven (1963), p. 41.
- ^ Bennett (2004), p. 322.
- ^ Murty (2014), p. 103.
- ^ Abramowitz (1965), p. 74.
- ^ Wintucky (1971), p. 6-7.
- ^ Gowers (2010), p. 307.
- ^ أ ب Thomas (1995), chapt. 8.9.
- ^ Ahlfors (1966), p. 43-44.
- ^ Vaughn (2007), p. 184.
- ^ Aigner (2000), p. 149.
- ^ Remmert (2001), p. 327.
- ^ Hijab (2016), p. 207.
- ^ أ ب Campos (2012), p. 18.
- ^ Gowers (2010), p. 307-308.
- ^ Pivato (2010), p. 243.
- ^ Kantabutra (1996), p. 328-339.
- ^ Lee (2004), p. 364.
- ^ Brent (1976), p. 242–251.
- ^ Abramowitz (1965), p. 72.
- ^ Gellert (1989), p. 264.
- ^ أ ب Pan (1964), p. 529-530.
- ^ Zwillinger (2011), p. 219.
- ^ Thomas (1995), p. 138.
- ^ Olver (2010), p. 116.
- ^ Hobson (1891), p. 39.
- ^ Sullivan (1988), p. 243.
- ^ Beyer (1996), p. 43-44.
- ^ Olver (2010), p. 121.
- ^ Beyer (1987), p. 323.
- ^ Árpád (2010), p. 14.
- ^ NIST (1952), p. V.
- ^ Schuyler (1875), p. 161.
- ^ Fogiel (1984), p. 143.
- ^ Larson (2011), p. 702.
- ^ Strang (1991), p. 389.
- ^ Peirce (1861), p. 400.
- ^ أ ب Folland (2009), p. 77.
- ^ Smith (1997), p. 481.
- ^ Tenenbaum (1985), p. 314.
- ^ Moebs (2016), p. 172.
- ^ Selezhnev (1963), p. 47.
- ^ أ ب King (1986), p. 83.
- ^ Oppenheim (2008), p. 583.
- وب
- ^ أ ب "Table of Domain and Range of Common Functions". analyzemath (بالإنجليزية). Archived from the original on 2019-02-08. Retrieved 2023-07-23.
- ^ J. J. O'Connor; E. F.Robertson. "Madhava of Sangamagrama". School of Mathematics and Statistics University of St Andrews (بالإنجليزية). Archived from the original on 2006-05-14. Retrieved 2007-09-08.
- ^ J. J. O'Connor; E. F. Robertson. "Abu Arrayhan Muhammad ibn Ahmad al-Biruni". School of Mathematics and StatisticsUniversity of St Andrews (بالإنجليزية). Archived from the original on 2020-07-17. Retrieved 2023-07-24.
- ^ J. J. O'Connor; E. F.Robertson. "Albert Girard". School of Mathematics and Statistics University of St Andrews (بالإنجليزية). Archived from the original on 2023-02-05. Retrieved 2023-07-25.
- ^ J. J. O'Connor; E. F. Robertson. "Thomas Fincke". School of Mathematics and StatisticsUniversity of St Andrews (بالإنجليزية). Archived from the original on 2017-01-07. Retrieved 2023-07-25.
- ^ Weisstein, Eric W. "Circular Functions". Wolfram Mathworld (بالإنجليزية). Archived from the original on 2017-04-03. Retrieved 2023-07-23.
- ^ أ ب Weisstein, Eric W. "Trigonometry Angles--Pi/9". Wolfram Mathworld (بالإنجليزية). Archived from the original on 2019-12-30. Retrieved 2023-07-25.
- ^ أ ب "Sine: Introduction to the trigonometric functions (subsection Trigonometrics/05)". Wolfram Research (بالإنجليزية). Archived from the original on 2016-05-02. Retrieved 2020-04-14.
- ^ Rowland, Todd; Weisstein, Eric W. "Pole". Wolfram Mathworld (بالإنجليزية). Archived from the original on 2020-03-18. Retrieved 2023-07-25.
- ^ Gandhi, Viswanathan (7 Oct 2014). "Domain coloring for visualizing complex functions". Gandhi Viswanathan's Blog (بالإنجليزية). Archived from the original on 2020-04-12. Retrieved 2023-07-28.
- ^ Alex Svirin. "Weierstrass Substitution". Math24 (بالإنجليزية). Archived from the original on 2020-03-27. Retrieved 2020-03-27.
- ^ Weisstein, Eric W. "Inverse Trigonometric Functions". Wolfram Mathworld (بالإنجليزية). Archived from the original on 2020-04-13. Retrieved 2023-07-28.
- ^ Weisstein, Eric W. "Gudermannian". Wolfram Mathworld (بالإنجليزية). Archived from the original on 2023-06-23. Retrieved 2023-07-28.
- ^ "Area of Triangle Using Trigonometry". mathbitsnotebook (بالإنجليزية). Archived from the original on 2019-10-29. Retrieved 2020-05-21.
- ^ Weisstein, Eric W. "Fourier Transform". Wolfram Mathworld (بالإنجليزية). Archived from the original on 2020-03-18. Retrieved 2023-07-28.
- ^ Weisstein, Eric W. "Lissajous Curve". Wolfram Mathworld (بالإنجليزية). Archived from the original on 2019-11-15. Retrieved 2023-07-25.
- ^ "Electrical Power in AC Circuits and Reactive Power". electronics-tutorials (بالإنجليزية). Archived from the original on 2019-07-12. Retrieved 2023-07-31.
- ^ Eli Maor; Raymond Walter Barnard. "Trigonometry" (بالإنجليزية). Encyclopedia Britannica. Archived from the original on 2023-10-19.
معلومات المراجع كاملة[عدل]
- الكتب
- بالعربية
- المعجم الموحد لمصطلحات الرياضيات والفلك: (إنجليزي - فرنسي - عربي)، سلسلة المعاجم الموحدة (3) (بالعربية والإنجليزية والفرنسية)، تونس: مكتب تنسيق التعريب، 1990، OCLC:4769958475، QID:Q114600477
- محمد علي التهانوي (1996)، موسوعة كشاف اصطلاحات الفنون والعلوم، ترجمة: عبد الله الخالدي؛ جورج زيناتي، مراجعة: رفيق العجم. تحقيق: علي دحروج، بيروت: مكتبة لبنان ناشرون، OCLC:36301759، QID:Q120808017
- مجد الدين الفيروز آبادي (1998)، القاموس المحيط، تحقيق: محمد نعيم العرقسوسي (ط. 6)، بيروت: مؤسسة الرسالة، OCLC:224868904، QID:Q120833288
- أبو الريحان البيروني (2002). القانون المسعودي. تحقيق: عبد الكريم سامي الجندي (ط. 1). بيروت: دار الكتب العلمية. ISBN:978-2-7451-3305-2. OCLC:51176204. QID:Q120829593.
- روبرت موير؛ فرانك أيرز (2004). حساب المثلثات: سلسلة ملخصات شوم إيزي. ترجمة: سعيد فرج إسكندر. مراجعة: انتصارات محمد حسن الشبكي. القاهرة: الدار الدولية للاستثمارات الثقافية. ISBN:978-977-282-145-7. OCLC:1227815506. QID:Q120776485.
- رشدي راشد؛ ريجيس مورلون، المحررون (2005). موسوعة تاريخ العلوم العربية. بيروت: مركز دراسات الوحدة العربية، مؤسسة عبد الحميد شومان. ISBN:9953-450-74-9. OCLC:834806113. QID:Q120867724.
- مصطفى الجيوسي (2005). موسوعة علماء العرب والمسلمين وأعلامهم. عَمَّان: دار أسامة للنشر والتوزيع. ISBN:978-65-00-00070-2. QID:Q120870193.
- ميشال إبراهيم ساسين؛ رامي أبو سليمان؛ فادي فرحات (2007). قاموس المصطلحات العلمية: فيزياء - كيمياء - رياضيات (إنكليزي - فرنسي - عربي) مع مسرد ألفبائي بالألفاظ الفرنسية (بالعربية والإنجليزية والفرنسية) (ط. 1). بيروت: دار الكتب العلمية. ISBN:978-2-7451-5445-3. OCLC:929661320. QID:Q120799140.
- منير البعلبكي؛ رمزي البعلبكي (2008). المورد الحديث: قاموس إنكليزي عربي (بالعربية والإنجليزية) (ط. 1). بيروت: دار العلم للملايين. ISBN:978-9953-63-541-5. OCLC:405515532. OL:50197876M. QID:Q112315598.
- محمد القوصي (2013). التكامل في الرياضيات. عَمَّان: مركز الكتاب الأكاديمي. ISBN:978-9957-35-052-9. QID:Q120802752.
- موفق دعبول؛ بشير قابيل؛ مروان البواب؛ خضر الأحمد (2018)، معجم مصطلحات الرياضيات (بالعربية والإنجليزية)، دمشق: مجمع اللغة العربية بدمشق، OCLC:1369254291، QID:Q108593221
- الكلنبوي (2019). رسائل الكلنبوي في علم الفلك: رسالة الربع المجيب ويليه رسالة في الارتفاع (في العمل بالربع المقنطرات) ويليه دقائق البيان في قبلة البلدان. تحقيق: أحمد فريد المزيدي. بيروت: دار الكتب العلمية. ISBN:978-2-7451-8540-2. OCLC:1229991269. QID:Q120828359.
{{استشهاد بكتاب}}: صيانة الاستشهاد: ref duplicates default (link)
- بالإنكليزية
- Benjamin Peirce (1861), An elementary treatise on plane & spherical trigonometry: with their applications to navigation, surveying, heights, and distances, and spherical astronomy, and particularly adapted to explaining the construction of Bowditch's navigator, and the nautical almanac (بالإنجليزية), Boston: John Munroe & Company, OCLC:4936622, OL:6930975M, QID:Q121033840
- Aaron Schuyler (1875), Plane and Spherical Trigonometry and Mensuration (بالإنجليزية), New York City: American Book Company, OCLC:903429791, QID:Q121030014
- Ernest William Hobson (1891), A treatise on plane and advanced trigonometry (بالإنجليزية), Cambridge: Cambridge University Press, OCLC:932543145, QID:Q121009322
- Tables of Chebyshev polynomials, Sn(x) and Cn(x) (بالإنجليزية), Washington, D.C.: National Institute of Standards and Technology, 1952, OCLC:459562958, QID:Q121028174
- Test and evaluation for airborne flexible gunnery systems (بالإنجليزية), United States Department of the Air Force, 1954, OCLC:966761086, QID:Q120912867
- Vasiliĭ Petrovich Selezhnev (1963), Navigation instruments (بالإنجليزية), Ohio: National Air and Space Intelligence Center, OCLC:609312702, QID:Q121070378
- The universal encyclopedia of mathematics (بالإنجليزية). London: Pan Books. 1964. ISBN:978-0-330-24396-4. OCLC:16545888. OL:10487717M. QID:Q121008744.
- Milton Abramowitz; Irene Stegun, eds. (1965). Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables (بالإنجليزية). New York City: Dover Publications. ISBN:978-0-486-61272-0. OCLC:429082. OL:21951925M. QID:Q120962780.
- Lars Ahlfors (1966), Complex analysis: an introduction of the theory of analytic functions of one complex variable (بالإنجليزية) (2nd ed.), New York City: McGraw Hill Book Company, OCLC:476286192, QID:Q120973648
- Kaj Leo Nielsen (1966), Logarithmic and other trigonometric tables (بالإنجليزية) (2nd ed.), New York City: Barnes & Noble, LCCN:61009103, OCLC:2679711, QID:Q120904032
- Ivan M. Niven (1963). "Irrational numbers". Carus Mathematical Monographs. Carus Mathematical Monographs (بالإنجليزية) (2nd ed.). New Jersey: The Mathematical Association of America (11). OCLC:1151828456. QID:Q120892716.
- Murray H. Protter; Charles B. Morrey, Jr. (1970), Lynn Harold Loomis (ed.), College calculus with analytic geometry (بالإنجليزية) (2nd ed.), Reading: Addison-Wesley, LCCN:76087042, OCLC:84977, QID:Q120917123
- Howard Eves (1983). Great moments in mathematics: before 1650 (بالإنجليزية) (2nd ed.). Washington, D.C.: Mathematical Association of America. ISBN:978-0-88385-310-8. OCLC:10646115. OL:14411085M. QID:Q120834208.
- Max Fogiel (1984). Handbook of mathematical, scientific, and engineering formulas, tables, functions, graphs, transforms (بالإنجليزية). New Jersey: Research and Education Association. ISBN:978-0-87891-521-7. OCLC:12081852. OL:1018042M. QID:Q120825513.
- Morris Tenenbaum; Harry Pollard (1985). Ordinary differential equations: an elementary textbook for students of mathematics, engineering, and the sciences (بالإنجليزية). New York City: Dover Publications. ISBN:978-1-62198-630-0. OCLC:849739582. QID:Q121059833.
- William H. Beyer, ed. (1987). Handbook of mathematical sciences (بالإنجليزية) (6th ed.). Boca Raton: CRC Press. ISBN:978-0-8493-0656-3. OCLC:1158112388. OL:18359343M. QID:Q121027833.
- Michael Sullivan (1988). Trigonometry (بالإنجليزية). San Francisco, London: Dellen Publishing Company, Macmillan Publishers. ISBN:978-0-02-418336-1. OCLC:17231755. OL:2402829M. QID:Q121009798.
- Walter Gellert; Siegfried Gottwald; Manfred Hellwich; Herbert Kästner; Herbert Küstner, eds. (1989). The VNR concise encyclopedia of mathematics (بالإنجليزية) (2nd ed.). New York City: Van Nostrand. ISBN:978-0-442-20590-4. OCLC:18986996. OL:2049524M. QID:Q120986539.
- John Simpson; Edmund Weiner, eds. (1989). The Oxford English Dictionary (بالإنجليزية) (2nd ed.). Oxford: Oxford University Press. ISBN:978-0-19-861186-8. OCLC:611410378. OL:18318791M. QID:Q120829013.
- Gilbert Strang (1991). Calculus (بالإنجليزية). Wellesley: Wellesley Publishers. ISBN:978-0-9614088-2-4. OCLC:30082655. OL:22619872M. QID:Q121033360.
- George B. Thomas; Ross L. Finney (1995). Calculus and Analytic Geometry (بالإنجليزية) (9th ed.). Reading: Addison-Wesley. ISBN:978-0-201-53174-9. OL:1105407M. QID:Q120969870.
- Roshdi Rashed; Régis Morelon (1996). Encyclopedia of the history of Arabic science (بالإنجليزية) (1st ed.). London: Routledge. ISBN:978-0-415-02063-3. OCLC:34731151. OL:6854328M. QID:Q120861506.
- Steven W. Smith (1997). Digital signal processing: a practical guide for engineers and scientists (بالإنجليزية). San Diego: California Technical Publishing. ISBN:978-0-9660176-3-2. OCLC:39229533. OL:712576M. QID:Q121055028.
- C. B. F. Walker, ed. (1999). Astronomy before the telescope (بالإنجليزية). London: British Museum. ISBN:978-0-7141-2733-0. OCLC:41258121. OL:9661970M. QID:Q120869372.
- Martin Aigner; Günter M. Ziegler (2000). Proofs from THE BOOK (بالإنجليزية) (2nd ed.). Berlin: Springer Berlin Heidelberg. ISBN:978-3-540-67865-6. OCLC:488918865. OL:6790193M. QID:Q120870100.
- H. H. Heng; Khoo Cheng; John F. Talbert (2001). Additional mathematics (بالإنجليزية). Central Area: Longman. ISBN:978-981-235-211-8. OCLC:68769222. OL:28985375M. QID:Q120884889.
- Reinhold Remmert (1991). "Theory of Complex Functions". Graduate Texts in Mathematics (بالإنجليزية). New York City: Springer Science+Business Media (122). DOI:10.1007/978-1-4612-0939-3. ISBN:978-0-387-97195-7. ISSN:0072-5285. OCLC:800300774. OL:1857322M. QID:Q120969645.
- Marlow Anderson; Victor J. Katz; Robin Wilson (2004). Sherlock Holmes in Babylon: And Other Tales of Mathematical History (بالإنجليزية). Washington, D.C.: Mathematical Association of America. ISBN:978-0-88385-546-1. OCLC:54028528. OL:3698735M. QID:Q120892530.
- Annette Imhausen; Eleanor Robson; Joseph Dauben; Kim Plofker; John Lennart Berggren (2007). Victor J. Katz (ed.). The mathematics of Egypt, Mesopotamia, China, India, and Islam: a sourcebook (بالإنجليزية). New Jersey: Princeton University Press. ISBN:978-0-691-11485-9. OCLC:71369310. OL:17235128M. QID:Q120905087.
- Robert Bradley; Lawrence A. D'Antonio; Charles Edward Sandifer, eds. (2007). Euler at 300: an appreciation (بالإنجليزية). Washington, D.C.: Mathematical Association of America. ISBN:978-0-88385-565-2. OCLC:166372994. OL:11232686M. QID:Q120906849.
- Michael Vaughn (2007). Introduction to mathematical physics (بالإنجليزية). Weinheim: Wiley-VCH. ISBN:978-3-527-40627-2. OCLC:141379117. OL:22763159M. QID:Q120973188.
- Victor J. Katz (2009). A history of mathematics: an introduction (بالإنجليزية) (3rd ed.). Boston: Addison-Wesley. ISBN:978-0-321-38700-4. OCLC:71006826. OL:10460797M. QID:Q120806397.
- Clifford A. Pickover (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics (بالإنجليزية). New York City: Sterling Publishing. ISBN:978-1-4027-5796-9. OCLC:800675813. OL:22652981M. QID:Q120885623.
- Kim Plofker (2008). Mathematics in India (بالإنجليزية). Princeton: Princeton University Press. ISBN:978-1-4008-3407-5. OCLC:232132000. OL:28999237M. QID:Q120828234.
- Gerald Folland (2009). Fourier analysis and its applications (بالإنجليزية). Providence: American Mathematical Society. ISBN:978-0-8218-4790-9. OCLC:1103642706. OL:22666320M. QID:Q121009509.
- Timothy Gowers; June Barrow-Green; Imre Leader, eds. (2010). The Princeton Companion to Mathematics (بالإنجليزية). Princeton University: Princeton University Press. DOI:10.1515/9781400830398. ISBN:978-1-4008-3039-8. OCLC:1113342992. OL:25921652M. QID:Q120968602.
- Steven G. Krantz (2010). An episodic history of mathematics: Mathematical culture through problem solving (بالإنجليزية). Washington, D.C.: The Mathematical Association of America. ISBN:978-0-88385-766-3. OCLC:802146883. OL:24334196M. QID:Q120833573.
- Frank W. J. Olver; Daniel W. Lozier; Ronald F Boisvert; Charles Winthrop Clark, eds. (2010). NIST handbook of mathematical functions (بالإنجليزية) (1st ed.). New York City: Cambridge University Press. ISBN:978-0-521-19225-5. OCLC:502037224. OL:26798864M. QID:Q120974205.
- Árpád Baricz (2010). "Generalized Bessel functions of the first kind". Lecture Notes in Mathematics (بالإنجليزية). Berlin: Springer Berlin Heidelberg. DOI:10.1007/978-3-642-12230-9. ISBN:978-3-642-12229-3. ISSN:0075-8434. OCLC:654398638. OL:25321429M. Zbl:1203.33001. QID:Q121027903.
- Ron Larson; Bruce H. Edwards (2010). Calculus of a Single Variable: early transcendental functions (بالإنجليزية). Boston: Cengage Group. ISBN:978-0-538-73552-0. OCLC:326626818. OL:25040979M. QID:Q121032244.
- Daniel Ian Zwillinger (2011). CRC Standard Mathematical Tables and Formulae (بالإنجليزية) (32nd ed.). Baton Rouge: CRC Press. ISBN:978-1-4398-3550-0. OCLC:1048010941. OL:33411251M. QID:Q121009020.
- Marcus Pivato (2010). Linear Partial Differential Equations and Fourier Theory (بالإنجليزية). Cambridge: Cambridge University Press. ISBN:978-0-511-76461-5. OCLC:664021417. OL:44885020M. QID:Q120985808.
- Michael R. Lindeburg (2012). Civil engineering reference manual for the PE Exam (بالإنجليزية) (13th ed.). Belfast: Professional Publications. ISBN:978-1-59126-380-7. OCLC:1153728411. OL:31099566M. QID:Q120913237.
- Ron Larson (2013). Trigonometry (بالإنجليزية) (9th ed.). Pacific Grove: Brooks/Cole Publishing. ISBN:978-1-285-60718-4. OCLC:811729667. QID:Q120918455.
- M. Ram Murty; Purusottam Rath (2014). Transcendental Numbers (بالإنجليزية). New York City: Springer Science+Business Media. DOI:10.1007/978-1-4939-0832-5. ISBN:978-1-4939-0832-5. OCLC:882553933. OL:37197259M. Zbl:1297.11001. QID:Q120965474.
- Geoffrey Berresford; Andrew Mansfield Rockett (2015). Applied calculus (بالإنجليزية). Boston: Cengage Group. ISBN:978-1-305-46505-3. OCLC:1141958672. QID:Q120913832.
- Omar Hijab (2016). Introduction to Calculus and Classical Analysis (بالإنجليزية) (4th ed.). Cham: Springer Science+Business Media. DOI:10.1007/978-3-319-28400-2. ISBN:978-3-319-28400-2. OCLC:939900301. OL:35801666M. Zbl:1332.26001. QID:Q120975301.
- William Moebs; Samuel J. Ling,; Jeff Sanny (2016). University Physics (بالإنجليزية). Houston: OpenStax. Vol. 1. ISBN:978-1-938168-27-7. OL:31971377M. QID:Q121067181.
{{استشهاد بكتاب}}: صيانة الاستشهاد: علامات ترقيم زائدة (link) - Elias C. Tonias; Constantine N. Tonias (2016). Geometric procedures for civil engineers (بالإنجليزية) (1st ed.). Switzerland: Springer Science+Business Media. DOI:10.1007/978-3-319-24295-8. ISBN:978-3-319-24295-8. OCLC:948511665. OL:37246454M. Zbl:1365.00003. QID:Q120885033.
- Alan V. Oppenheim; Alan Steven Willsky; Hamid Nawab (2008). Signals & Systems (بالإنجليزية) (2nd ed.). Prentice-Hall of India Private Limited. ISBN:978-81-203-1246-3. OCLC:1288493903. OL:13129224M. QID:Q121863124.
- Eli Maor (2002). Trigonometric Delights (بالإنجليزية). Princeton University Press. ISBN:978-0-691-09541-7. OL:7758279M. QID:Q121916112.
- King, David A. (1986). "Ḳibla: Astronomical Aspects". In Bosworth, C. E.; van Donzel, E.; Lewis, B.; Pellat, Ch. (eds.). The Encyclopaedia of Islam, New Edition, Volume V: Khe–Mahi (بالإنجليزية). Leiden: E. J. Brill. ISBN:90-04-07819-3.
- تقارير ومقالات ودوريات محكمة
- العربية
- "مصطلحات في علم الرياضة". مجلة مجمع اللغة العربية. ج. 8: 282–294. 1955. QID:Q120964344.
- خضر الأحمد (2004). "دالة (تابع)". الموسوعة العربية. ج. 9: 164–170. QID:Q120824978.
- باسل شكر محمود؛ إحسان عبد الستار علي (2011). "التنفیذ المادي باستخدام FPGA لخوارزمیتي كوردك وجدول المقارنة لحسابالدوال الریاضیة الأولیة". مجلة هندسة الرافدين. ج. 19 ع. 2: 50–71. DOI:10.33899/RENGJ.2011.27044. ISSN:2220-1270. OCLC:8520333370. QID:Q120885449.
- بالفرنسية
- Youcef Guergour (2005). "Le roi de Saragosse al-Mu'taman Ibn Hûd (m. 1085) et le théorème de Pythagore: ses sources et ses prolongements" (PDF). Llull (بالفرنسية). 28 (62): 415–434. ISSN:0210-8615. OCLC:810471504. S2CID:191124306. QID:Q120870525.
- الإنكليزية
- Edwin Wintucky (1971), Formulas for nth order derivatives of hyperbolic and trigonometric functions (PDF) (بالإنجليزية), Washington, D.C.: National Aeronautics and Space Administration, OCLC:249418715, QID:Q120965784
- Norman Schaumberger (1974). "A Classroom Theorem on Trigonometric Irrationalities". The Two-Year College Mathematics Journal (بالإنجليزية). 5 (1): 73. DOI:10.2307/3026991. ISSN:0049-4925. JSTOR:3026991. OCLC:5548730043. QID:Q54293679.
- Richard P. Brent (1976). "Fast Multiple-Precision Evaluation of Elementary Functions". Journal of the ACM (بالإنجليزية). 23 (2): 242–251. DOI:10.1145/321941.321944. ISSN:0004-5411. Zbl:0324.65018. QID:Q55887322.
- Bibhutibhusan Datta; Avadhesh Narayan Singh (1983). Kripa shankar shukla (ed.). "Hindu trigonometry" (PDF). Indian Journal of History of Science (بالإنجليزية). 18 (1): 39–108. ISSN:0019-5235. OCLC:1101587714. QID:Q120833133.
- Owen Gingerich (1986). "Islamic Astronomy". Scientific American (بالإنجليزية). 254 (4): 74–83. DOI:10.1038/SCIENTIFICAMERICAN0486-74. ISSN:0036-8733. JSTOR:24975932. OCLC:7792893706. QID:Q55880842.
- Carl Benjamin Boyer (1991). A history of mathematics (بالإنجليزية). Reviewer: Uta Caecilia Merzbach (2nd ed.). New York City: Wiley. ISBN:978-0-471-54397-8. OCLC:23823042. OL:18198047M. QID:Q120867638.
- W. A. Beyer; J. D. Louck; D. Zeilberger (1996). "Math Bite: A Generalization of a Curiosity that Feynman Remembered All His Life". Mathematics Magazine (بالإنجليزية). 69 (1): 43–44. DOI:10.1080/0025570X.1996.11996378. ISSN:0025-570X. JSTOR:2691393. OCLC:6067251629. QID:Q121009655.
- Vitit Kantabutra (1996). "On hardware for computing exponential and trigonometric functions". IEEE Transactions on Computers (بالإنجليزية). Institute of Electrical and Electronics Engineers. 45 (3): 328–339. DOI:10.1109/12.485571. ISSN:0018-9340. OCLC:8558276926. Zbl:1057.68502. QID:Q120906550.
- Jacques Sesiano (2000), Islamic Mathematics (بالإنجليزية), Springer Science+Business Media, pp. 137–165, DOI:10.1007/978-94-011-4301-1_9, OCLC:5894598435, QID:Q120836269
- Curtis D. Bennett; A. M. W. Glass; Gabor J. Szekely (2004). "Fermat's Last Theorem for Rational Exponents". American Mathematical Monthly (بالإنجليزية). 111 (4): 322. DOI:10.2307/4145241. ISSN:0002-9890. JSTOR:4145241. OCLC:7376764007. Zbl:1138.11317. QID:Q54000176.
- Dong-U Lee,; Oskar Mencer,; David J. Pearce; Wayne Luk (2004). "Automating Optimized Table-with-Polynomial Function Evaluation for FPGAs". Field Programmable Logic and Application, 14th International Conference , FPL 2004, Leuven, Belgium, August 30-September 1, 2004. International Conference on Field-Programmable Logic and Applications (بالإنجليزية). Springer Science+Business Media. 3203: 364–373. DOI:10.1007/978-3-540-30117-2_38. ISBN:978-3-540-22989-6. OCLC:5937763985. QID:Q120885371.
{{استشهاد بدورية محكمة}}: صيانة الاستشهاد: علامات ترقيم زائدة (link) - Jean-Pierre Merlet (2004). "A Note on the History of Trigonometric Functions". International Symposium on History of Machines and Mechanisms (بالإنجليزية). Springer Science+Business Media: 195–200. DOI:10.1007/1-4020-2204-2_16. ISBN:978-1-4020-2203-6. QID:Q54049142.
- Denis Roegel (2010), A reconstruction of Gunter's Canon triangulorum (بالإنجليزية), OCLC:711133129, QID:Q120867342





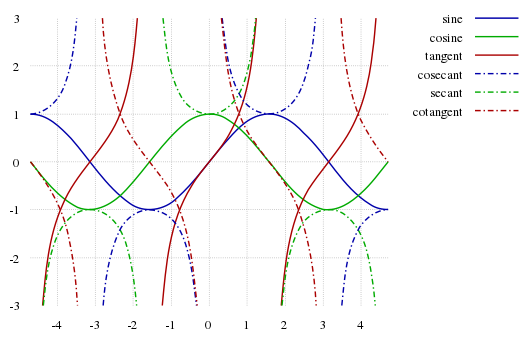





![{\displaystyle {\begin{cases}y(0)=0\\[2pt]y\,'(0)=1\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16813921748f6ec71b28a7f12ab8838419af6945)
![{\displaystyle {\begin{cases}y(0)=1\\[2pt]y\,'(0)=0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bef0fe0345ca1ff81f60cd36d710acf4f111726)














![{\displaystyle {\begin{aligned}\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[8pt]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1},\\[8pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d750b214306980413f88142bf78e7556b24f8d8)








































![{\displaystyle \left]-{\frac {\pi }{2}},{\frac {\pi }{2}}\right[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6b123273d134ae0a355186bca3947bf36996ceb)
![{\displaystyle {\begin{aligned}\operatorname {gd} x\int _{0}^{x}\operatorname {sech} t\,\mathrm {d} t=\arcsin \left(\tanh x\right)=\arctan(\sinh x)=\operatorname {arccsc} (\coth x)\\[6pt]\operatorname {sgn}(x)\arccos \left(\operatorname {sech} x\right)=\operatorname {sgn}(x)\operatorname {arcsec} (\cosh x)\\[6pt]2\arctan \left(\tanh {\frac {x}{2}}\right)\\[6pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a783e38d4eb4df4a23bab249478b8d4508faaae2)




















![{\displaystyle {\begin{aligned}e^{i\theta }&=\cos \theta +i\sin \theta \\[5pt]e^{-i\theta }&=\cos \theta -i\sin \theta .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b55517104c78856e37c60ba04ac30cabda0991d7)


























![{\displaystyle \mathrm {AB} =R\arccos \left[\sin \lambda _{\mathrm {A} }\,\sin \lambda _{\mathrm {B} }+\cos \lambda _{\mathrm {A} }\,\cos \lambda _{\mathrm {B} }\,\cos \left(L_{\mathrm {A} }-L_{\mathrm {B} }\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36b154a08ca72d68bde58243a17f2964c0c0056b)











