توزيع احتمالي طبيعي

من ويكيبيديا، الموسوعة الحرة
اذهب إلى: تصفح، ‏ بحث
التوزيع الطبيعي
دالة الكثافة الاحتمالية
دالة الكثافة الاحتمالية للتوزيع الطبيعي
الخط الأخضر يمثل التوزيع الاحتمالي الطبيعي الموسّط المختزل
دالة التوزيع التراكمي
دالة التوزيع التراكمي 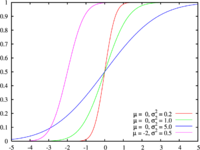للتوزيع الاحتمالي الطبيعي
المؤشرات \mu موقع (عدد حقيقي)
\sigma^2>0 مقياس تربيعي (عدد حقيقي)
الدعم x \in ]-\infty;+\infty[ \!
د۔ك۔ح۔ \frac1{\sigma\sqrt{2\pi}}\; \exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2} \right) \!
د۔ت۔ت \frac12 \left(1 + \mathrm{erf}\,\frac{x-\mu}{\sigma\sqrt2}\right) \!
المتوسط الحسابي \mu
الوسيط الحسابي \mu
المنوال \mu
التباين \sigma^2
التجانف 0
التفرطح 3 (حالة توزيع طبيعي)

0 (في حالة توزيع طبيعي موسّط ومختزل)
الاعتلاج \ln\left(\sigma\sqrt{2\,\pi\,e}\right)\!
د۔م۔ع M_X(t)= \exp\left(\mu\,t+\sigma^2 \frac{t^2}{2}\right)
الدالة المميزة \phi_X(t)=\exp\left(\mu\,i\,t-\frac{\sigma^2 t^2}{2}\right)
معلومات فيشر {{{معلومات فيشر}}}

في نظرية الاحتمالات، التوزيع الطبيعي (أو الغاوسي) هو توزيع احتمالي مستمر يستخدم غالباً كتقريب أولي لوصف المتغيرات العشوائية التي تميل إلى التمركز حول قيمة متوسطة وحيدة. إن لمخطط تابع كثافة الاحتمال المقابل لهذا التوزيع شكل الجرس، ويعرف بالتابع الغاوسي أو منحني الجرس.

f(x) = \tfrac{1}{\sqrt{2\pi\sigma^2}}\; e^{ -\frac{(x-\mu)^2}{2\sigma^2} },

حيث μ هو القيمة المتوقعة (مكان الذروة)، وσ 2 هو التباين (قياس عرض التوزيع). عندما تكون قيم وسيطي التوزيع μ = 0 وσ 2 = 1 فإنه يسمى التوزيع الطبيعي المعياري.

يعد التوزيع الطبيعي التوزيع الاحتمالي المستمر الأساسي، نظراً لدوره في مبرهنة النهاية المركزية، كما أنه من أول التوزيعات المستمرة التي تدرس في مقررات الإحصاء الابتدائية. فوفقاً لمبرهنة النهاية المركزية، وتحت شروط معينة، فإن مجموع عدد من المتغيرات العشوائية بعدد منته من المتوسطات والتباينات يقارب توزيعاً طبيعياً بازدياد عدد تلك المتغيرات. ولهذا السبب، فإنه كثيراً ما يشاهد هذا التوزيع في الممارسة العملية، وهو يستخدم في الإحصاء، والعلوم الطبيعية، والعلوم الاجتماعية [1] كنموذج بسيط للتعامل مع ظواهر معقدة. وعلى سبيل المثال، فإن خطأ الملاحظة في تجربة ما، غالباً ما يتبع توزيعاً طبيعية. كما يحسب انتشار اللايقين propagation of uncertainty باستخدام هذا الافتراض أيضاً.

لاحظ أن لمتغير ذي توزع طبيعي توزيعاً متناظراً حول متوسطه. ولهذا فإن القيم التي تنمو بشكل أسي (كالأسعار، والدخول، وعدد السكان) تكون ملتوية نحو يمين (skewness)، وبالتالي يمكن التعبير عنها بشكل أفضل باستخدام توزيعات أخرى، كالتوزيع الطبيعي اللوغاريتمي log-normal distribution، وتوزيع بارتو Pareto distribution.

محتويات

التوزيع الطبيعي الموسّط المختزل [عدل]

الدالّة \varphi : \R \to \R^+ بحيث \varphi(t)=\frac{1}{\sqrt{2\;\pi}}\, \mathrm{e}^{-\frac{t^2}{2}}

هي دالة كثافة احتمالية : هي متواصلة وتكاملها على \ \R يساوي 1.

فاننا نعلم أن \ \int_{-\infty}^{+\infty}\mathrm{e}^{-\frac{t^2}{2}}\ dt = \sqrt{2\, \pi} (تكامل غاوس).

ونبين أن (انظر التالي) التوزيع الذي يقع تحديده انطلاقا من دالة الكثافة هذه له قيمة متوقعة تساوى 0 وتباينا يساوي 0.

ملاحظات

  • الكثافة \varphi نظيرة
  • يمكن اشتقاق هذه الدالة عددا لا متناهيا من المرّات وتحقق مهما كان \ t \in \R المعادلة التالية \varphi'(t) = - t\, \varphi(t).

التعريف [عدل]

نسمي التوزيع الطبيعي (أو غاوسي) موسّط مختزل التوزيع المعرّف بدالة الكثافة \varphi.

الرسم البياني لهذه الكثافة يمثل شكل جرس.

خصائص التوزيع الاحتمالي الطبيعي [عدل]

  • القيم الأكثر تكراراً تقع في مركز التوزيع
  • كل من المتوسط، الوسيط، والمنوال يقع في مركز التوزيع
  • القيم البعيدة عن المتوسط ذات تكرار أقل
  • مجموع تكرارات القيم التي هي أكبر من المتوسط يساوي مجموع تكرارات القيم التي تحته
  • توجد علاقة معروفة بين نسبة المشاهدات (p) التي تقع ضمن مجال يبعد عن المتوسط بمقدار (z) من الانحرافات المعيارية

دالة التوزيع التراكمي [عدل]

لتكن \Phi دالة التوزيع التراكمي (Cumulative distribution function-Fonction de répartition) للتوزيع الموسّط المختزل. تحدد لكل عدد حقيقي x ب:

\ \Phi(x) = \int_{-\infty}^x \varphi(t)\, dt = \int_{-\infty}^x\frac{1}{\sqrt{2\,\pi}}\,\mathrm{e}^{-\frac{t^2}{2}}\, dt .

وهي تكامل \varphi ونهايتها في -\infty تساوي 0، ولا يمكن كتابتها باستعمال الدالات المعروفة (أس، جيب..) ولكن تصبح هي بنفسها دالة مستعملة بكثرة ومهمّة لكلّ من يمارس حساب الاحتمالات والإحصاء.

خاصيات الدالة \Phi :

  • قابلة للاشتقاق بعدد غير متناهي من المرّات و\Phi' = \varphi.
  • نامية حصريا وتنتهي إلى 0 في -\infty وإلى 1 في +\infty.

مراجع [عدل]

  1. ^ Gale Encyclopedia of Psychology — Normal Distribution

انظر أيضاً [عدل]

Portal-puzzle.svg بوابة إحصاء

—== قراءات ==

Nagaoka,Hiroshi (2000). Methods of information geometry. Oxford University Press. ISBN 0-8218-0531-2.
  • Bernardo,J. M.
Smith,A.F.M. (2000). Bayesian Theory. Wiley. ISBN 0-471-49464-X.
et al (1968). Computer approximations. New York: John Wiley & Sons, Inc. ISBN 0882756427.
Murray (1994). The bell curve: intelligence and class structure in American life. Free Press. ISBN 0-02-914673-9.
Kotz,S.
Balakrishnan,N. (1994). Continuous univariate distributions, Volume 1. Wiley. ISBN 0-471-58495-9.
  • Johnson,N.L.
Kotz,S.
Balakrishnan,N. (1994). Continuous univariate distributions, Volume 2. Wiley. ISBN 0-471-58494-0.
  • Kruskal,William H.
Stigler,Stephen M. (1997). Normative terminology: ‘normal’ in statistics and elsewhere. Statistics and public policy, edited by Bruce D. Spencer. Oxford University Press. ISBN 0-19-852341-6.
Read,Campbell B. (1996). Handbook of the normal distribution. ISBN 0824715411.
Severo,Norman C. (1964). Probability functions (chapter 26). Handbook of mathematical functions with formulas, graphs, and mathematical tables, by Abramowitz and Stegun
National Bureau of Standards. New York: Dover. ISBN 0-486-61272-4. http://www.math.sfu.ca/~cbm/aands/page_931.htm.
مشاريع شقيقة المزيد من الصور والملفات في كومنز عن: توزيع احتمالي طبيعي
ع · ن · ت
بعض التوزيعات الاحتمالية الشائعة بمتغير واحد
مستمرة
متقطعة

تم الاسترجاع من "http://ar.wikipedia.org/w/index.php?title=توزيع_احتمالي_طبيعي&oldid=10989026"