توزيع ستيودنت الاحتمالي

توزيع ستيودنت (توزيع T)

دالة الكثافة الاحتمالية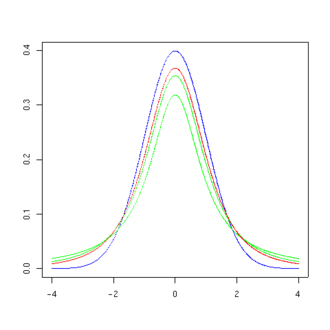
دالة التوزيع التراكمي
المؤشرات	$\nu >0$ درجة الحرية (عدد حقيقي)
الدعم	${\displaystyle x\in (-\infty$ ;+\infty )\!}
د۔ك۔ح۔	${\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}\left(1+{\frac {x^{2}}{\nu }}\right)^{-({\frac {\nu +1}{2}})}\!$
د۔ت۔ت	${\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\cdot \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma ({\frac {\nu }{2}})}}\end{matrix}}$ في حالة $\,_{2}F_{1}$ دالة فوق هندسية
المتوسط الحسابي	${\text{ }}\nu >1$,
الوسيط الحسابي	$0$
المنوال	$0$
التباين	${\frac {\nu }{\nu -2}}{\text{ }}\nu >2\!$
التجانف	${\text{ }}\nu >3$
التفرطح	${\frac {6}{\nu -4}}{\text{ for }}\nu >4\!$
الاعتلاج	${\begin{matrix}{\frac {\nu +1}{2}}\left[\psi ({\frac {1+\nu }{2}})-\psi ({\frac {\nu }{2}})\right]\\[0.5em]+\log {\left[{\sqrt {\nu }}B({\frac {\nu }{2}},{\frac {1}{2}})\right]}\end{matrix}}$ $\psi$: دالة ثنائي غاما, $B$: دالة بيتا
د۔م۔ع	غير معرفة
الدالة المميزة	غير معرفة
معلومات فيشر	{{{معلومات فيشر}}}

في الإحصاء ونظرية الاحتمالات، يعتبر توزيع ستيودنت (الإنجليزية: Student's t-distribution) أحد التوزيعات الاحتمالية المهمة الذي تنشأ عند تقدير المتوسط الحسابي لمجتمع احصائي ذي توزيع طبيعي عندما تكون حجم العينة صغيرا ، عادة أقل من 30 شخص.

مثال:

• توزيع درجات النجاح بين تلاميذ فصل . تجد أن 2/3 عدد التلاميذ لهم تقديرات متوسطة (قرب قمة التوزيع) ، وإلى أقصى اليسار تجد عدد قليل من الراسبين ، وإلى أقصى اليمين تجد عددا قليلا أيضا من الناجحين بتفوق.

التوزيع التراكمي

الشكل السفلي يبين التوزيع التراكمي. وهو ينشأ من جمع جميع القيم بين -4 إلى -3 إلى -2 ....إلى +3 إلى +4.

انظر أيضا

• توزيع خي تربيع (توزيع مربع كاي)
• توزيع أف
• توزيع غاما