عدد حقيقي
| صنف فرعي من | |
|---|---|
| جزء من | |
| يدرسه | |
| النقيض |


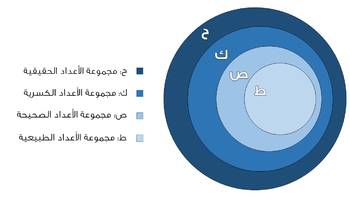
العدد الحقيقي (بالإنجليزية: Real number) في الرياضيات هو رقم يستخدم لقياس كميّة مستمرة [3][4][5] أحادية البعد مثل المسافة أو المدة أو درجة الحرارة.كلمة مستمر هنا تعني أنّه يمكن أن تحتوي على اختلافات صغيرة عشوائية. [أ]يمكن تمثيل كل رقم حقيقي بشكل فريد تقريبًا من خلال توسيع عشري لانهائي. [ب] [6] ظهرت كلمة حقيقي للمرة الأولى في القرن السابع عشر بواسطة رينيه ديكارت ، الذي ميز بين الجذور الحقيقية والخيالية لكثيرات الحدود.[بحاجة لمصدر] مجموعة الأعداد الحقيقية هي مجموعة أعداد تتكون من مجموعة الأعداد غير الكسري (R\Q) ومجموعة الأعداد الكسرية المنتهية والاعداد الكسرية المتكررة أو الدورية (Q). تشمل مجموعة الأعداد الكسرية مجموعة الأعداد الصحيحة (Z) والكسور، وتشمل مجموعة الأعداد الصحيحة مجموعة الأعداد الطبيعية (N). وبذلك تكون:
مجموعة الأعداد الطبيعية مجموعة جزئية من مجموعة الأعداد الصحيحة والأخيرة مجموعة جزئية من مجموعة الأعداد الكسرية والأخيرة مجموعة جزئية من مجموعة الأعداد الحقيقية.
مجموعة الأعداد الطبيعية تبدأ من الصفر إلى موجب ما لا نهاية بزيادة واحد صحيح في كل مرة،,وعرفت بهذا الاسم كوننا يمكن ملاحظتها في الطبيعة من حولنا؛ أما مجموعة الأعداد الصحيحة فتشتمل على الأعداد من سالب ما لا نهاية بالإضافة إلى مجموعة الأعداد الطبيعية بزيادة واحد صحيح كل مرة، أما الأعداد الكسرية فتتكون من كسور الأعداد الصحيحة في صورة بسط ومقام، أما الأعداد الحقيقية فتشمل المجموعات السابقة كلها بالإضافة إلى الأعداد التي لا يمكن كتابتها على شكل كسور مثل الπ (الباي) أي الأعداد اللا كسرية,والجذر التربيعي الذي لا يعطي رقمًا صحيحًا مثل جذر2
يمكن تصور الأعداد الحقيقية بأنها أعداد غير متناهية على خط مستقيم. وتأخذ الأعداد الحقيقية اسمها من تضادها مع فكرة الأعداد التخيلية. كما يمكن لها أن تقوم بقياس الكميات المستمرة على اختلافها. يمكن التعبير عنها بالكسور العشرية التي تكون عادة سلسلة من الأرقام غير منتهية وغير دورية في حالة الأرقام غير الكسرية أو الدورية في حالة الأعداد الكسرية. نشأت فكرة الأعداد الحقيقية بسبب وجود أطوال لا يمكن التعبير عن قياسها باستعمال أعداد صحيحة أو أعداد كسرية.
في هذه المجموعة المعادلة الآتية: لها حل.
خصائص أساسية[عدل]

العدد الحقيقي قد يكون كسريا أو غير كسري وقد يكون جبريا أو متساميا وقد يكون موجبا أو سالبا أو مساويا للصفر. تستعمل الأعداد الحقيقية من أجل قياس الكميات المتصلة.
وبشكل رسمي، لمجموعة الأعداد الحقيقية خاصيتان أساسيتان اثنتان هما كونها حقلا مرتبا، وكونها مكتملة.
أي رقم حقيقي غير صفري (لا يساوي صفر) هو إما سالب أو موجب.
مجموع وحاصل ضرب عددين حقيقيين غير سالبين هو مرة أخرى رقم حقيقي غير سالب، أي أنهما مغلقان في ظل هذه العمليات، ويشكلان مخروطًا موجبًا، مما يؤدي إلى ظهور ترتيب خطي للأرقام الحقيقية على طول الرقم خط.
تشكل الأعداد الحقيقية مجموعة لا نهائية من الأرقام التي لا يمكن تعيينها عن طريق مجموعة لا نهائية من الأعداد الطبيعية، أي أن هناك عددًا لا نهائيًا من الأعداد الحقيقية، بينما تسمى الأعداد الطبيعية اللانهائية. هذا يثبت أنه بشكل ما، هناك أعداد حقيقية أكثر من العناصر الموجودة في أي مجموعة قابلة للعد.
يمكن استخدام الأعداد الحقيقية للتعبير عن قياسات الكميات المستمرة. يمكن التعبير عنها من خلال التمثيلات العشرية، ومعظمها يحتوي على تسلسل لا نهائي من الأرقام على يمين الفاصلة العشرية ؛ غالبًا ما يتم تمثيل هذه الأرقام مثل ...324.823122147 ، حيث تشير علامة الحذف (ثلاث نقاط) إلى أنه لا يزال هناك المزيد من الأرقام في المستقبل. هذا يلمح إلى حقيقة أنه يمكننا أن نشير بدقة إلى عدد قليل فقط من الأرقام الحقيقية المختارة مع عدد كبير من الرموز.
بشكل أكثر رسمية، تحتوي الأرقام الحقيقية على خاصيتين أساسيتين لكونها حقل مرتب، ولها خاصية الحد الأعلى الأقل. الأول يقول أن الأعداد الحقيقية تشمل حقلاً، بالإضافة إلى الضرب وكذلك القسمة على أرقام غير صفرية، والتي يمكن ترتيبها بالكامل على خط الأعداد بطريقة متوافقة مع الجمع والضرب. الثانية تقول أنه إذا كان لمجموعة غير فارغة من الأعداد الحقيقية حد أعلى، فإن لها حدًا أعلى حقيقيًا. الشرط الثاني يميز الأرقام الحقيقية عن الأرقام المنطقية: على سبيل المثال، مجموعة الأرقام المنطقية التي يكون مربعها أقل من 2 هي مجموعة ذات حد أعلى (على سبيل المثال 1.5) ولكن لا يوجد حد أعلى (منطقي): ومن هنا تأتي الأرقام المنطقية لا تفي بأقل خاصية للحد الأعلى.
في الفيزياء[عدل]
في الفيزياء تستعمل الأعداد الحقيقية للتعبير عن المقاييس وذلك لسببين أساسيين:
- نتيجة الحسابات الفيزيائية لا يعبر عنها بأعداد كسرية غالبا، دون أن يأخذها الفيزيائيون بعين الاعتبار في استدلالاتهم وذلك لأنها لا تحمل أي معنى فيزيائي.
- نجد مفاهيم كالسرعة اللحظية والتسارع في الفيزياء. وهذه المفاهيم ناتجة عن نظريات رياضية التي تهتم كثيرا بالأعداد الحقيقية وتعتبرها كحاجة نظرية. بالإضافة إلى أن هاته المفاهيم تكون أكثر دقة وأهمية إذا ما تم التعبير عنها بأعداد حقيقية.
بالمقابل لا يمكن الاكتفاء بأعداد دقتها غير منتهية في المقاييس الفيزيائية. لذلك يتم تقريب هاته الأعداد بحسب الحاجة إلى أعداد عشرية.
لذلك إذا قام الفيزيائيون بحسابات في R، فهم يحتاجون إلى التعبير عن النتائج بالأعداد العشرية.
يتم استخدام الأرقام الحقيقية لقياس معظم الثوابت الفيزيائية مثل ثابت الجاذبية العامة والمتغيرات الفيزيائية مثل الموقع، الكتلة، السرعة والشحنة الكهربائية. في الواقع، يتم وصف النظريات الفيزيائية الأساسية مثل الميكانيكا الكلاسيكية ، والكهرومغناطيسية، وميكانيكا الكم، والنسبية العامة، والنموذج القياسي باستخدام الهياكل الرياضية، وعادة ما تكون الفتحات الملساء أو مساحات هلبرت ، والتي تستند إلى الأرقام الحقيقية، على الرغم من القياسات الفعلية للكميات المادية هي ذات دقة متناهية.
اقترح الفيزيائيون من حين لآخر أن نظرية أكثر جوهرية من شأنها أن تحل محل الأعداد الحقيقية بكميات لا تشكل سلسلة متصلة، لكن مثل هذه المقترحات تظل تخمينية.
في الحاسوب[عدل]
لا يمكن لحاسبات الحاسوب أن تعمل على كل الأعداد الحقيقية، بل تعمل على مجموعة جزئية فقط من الأعداد الحقيقية. يحدها في ذلك عدد البتات الموجودة في الحاسوب من أجل خزن ومعالجة الأعداد الحقيقية.
التاريخ[عدل]
اسعملت الكسور الاعتيادية من طرف المصريين قبل ألف سنة قبل الميلاد. في حوال 500 ق.م، بين علماء الرياضيات الإغريقين بقيادة فيثاغورس الحاجة إلى الأعداد غير الكسرية.
التعريف[عدل]
هو اتحاد مجموعة الأعداد الكسرية والأعداد غير الكسرية.
البناء انطلاقا من الأعداد الكسرية[عدل]
يمكن للأعداد الحقيقية أن تنشأ تكميلا للأعداد الكسرية حيث تؤول كل متتالية معرفة بسلسلة من الأعداد العشرية أو الثنائية كما هو الحال بالنسبة ل {3, 3.1, 3.14, 3.141, 3.1415,...}، إلى عدد حقيقي ما.
للمزيد من المعلومات ومن أجل التطرق إلى إنشاءات أخرى للأعداد الحقيقية، انظر إلى إنشاء الأعداد الحقيقية.
خصائص[عدل]
الاكتمال[عدل]
من أسباب استعمال الأعداد الحقيقية كونها تحتوي على جميع النهايات.
- كل متتالية لكوشي من الأعداد الحقيقية، هي متتالية متقاربة.
الأعداد الحقيقية في نظرية المجموعات[عدل]
انظر إلى فضاء بير (نظرية المجموعات)
ملاحظات[عدل]
- ^ هذا لا يكفي لتمييز الأعداد الحقيقية عن العدد المنطقي ؛ مطلوب أيضًا خاصية الاكتمال.
- ^ The terminating rational numbers may have two decimal expansions (see 0.999...); the other real numbers have exactly one decimal expansion.
انظر أيضًا[عدل]
- اكتمال الأعداد الحقيقية
- سيمون ستيفين
- الكسور المستمرة
- العدد التخيلي
- نهاية متتالية
- الأعداد المركبة
- التحليل الحقيقي
- معيار المصفوفة
- متطابقات هامة
المراجع[عدل]
- ^ أ ب ت وصلة مرجع: https://mathworld.wolfram.com/RealNumber.html.
- ^ وصلة مرجع: https://www.britannica.com/science/real-number.
- ^ "معلومات عن عدد حقيقي على موقع thes.bncf.firenze.sbn.it". thes.bncf.firenze.sbn.it. مؤرشف من الأصل في 2019-04-17.
- ^ "معلومات عن عدد حقيقي على موقع id.loc.gov". id.loc.gov. مؤرشف من الأصل في 2019-12-10.
- ^ "معلومات عن عدد حقيقي على موقع d-nb.info". d-nb.info. مؤرشف من الأصل في 2019-12-10.
- ^ "Real number". Oxford Reference. 3 أغسطس 2011. مؤرشف من الأصل في 2023-04-04.
| في كومنز صور وملفات عن: عدد حقيقي |

