توزيع وايبول

توزيع وايبول

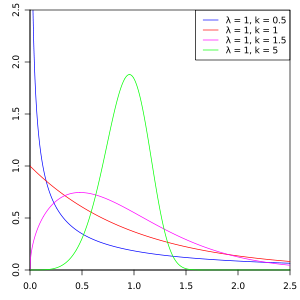
دالة الكثافة الاحتمالية
دالة التوزيع التراكمي
المؤشرات	$\lambda>0\,$ (حقيقي) $k>0\,$ (حقيقي)
الدعم	$x \in [0; +\infty)\,$
د۔ك۔ح۔	$f(x)=\begin{cases} \frac{k}{\lambda}\left(\frac{x}{\lambda}\right)^{k-1}e^{-(x/\lambda)^{k}} & x\geq0\\ 0 & x<0\end{cases}$
د۔ت۔ت	$1- e^{-(x/\lambda)^k}$
المتوسط الحسابي	$\lambda \, \Gamma(1+1/k)\,$
الوسيط الحسابي	$\lambda(\ln(2))^{1/k}\,$
المنوال	$\lambda \left(\frac{k-1}{k} \right)^{\frac{1}{k}}\,$ إذا $k>1$
التباين	$\lambda^2\Gamma(1+2/k) - \mu^2\,$
التجانف	$\frac{\Gamma(1+3/k)\lambda^3-3\mu\sigma^2-\mu^3}{\sigma^3}$
التفرطح	$\gamma_2=\frac{\lambda^4\Gamma(1+\frac{4}{k})-4\mu\sigma^3\gamma_1-3\sigma^4-6\mu^2\sigma^2-\mu^4}{\sigma^4}$
الاعتلاج	$\gamma(1-1/k)+\ln(\lambda/k)+1 \,$
د۔م۔ع	$\sum_{n=0}^\infty \frac{t^n\lambda^n}{n!}\Gamma(1+n/k), \ k\geq1$
الدالة المميزة	$\sum_{n=0}^\infty \frac{(it)^n\lambda^n}{n!}\Gamma(1+n/k)$
معلومات فيشر	{{{معلومات فيشر}}}

في نظرية الاحتمالات والإحصاء، توزيع وايبول توزيع احتمالي مستمر اشتق اسمه من اسم المهندس والرياضياتي والدي وايبول. ويستعمل لأول مرة سنة لوصف توزع أحجام الجسيمات.

الخواص

دالة الكثافة

يقال أن لمتغير لعشوائي ما أنه يتبع توزيع وايبول إذا كانت دالة كثافته تعطى بالشكل التالي:

$f(x;\lambda,k) = \begin{cases} \frac{k}{\lambda}\left(\frac{x}{\lambda}\right)^{k-1}e^{-(x/\lambda)^{k}} & x\geq0 ,\\ 0 & x<0 ,\end{cases}$

حيث k > 0 و λ >0 متثابتا التوزيع.

دالة التوزيع

دالة التوزيع التراكمي لمتغير عشوائي يتبع توزيع وايبول تعطى بالشكل التالي:

$F(x;k,\lambda) = 1- e^{-(x/\lambda)^k}\,$

لكل x ≥ 0, و F(x; k; λ) = 0 لـ x < 0.

أما معدل العطب أو (معدل الخطر) فيعطى بالصيغة التالية.

$h(x;k,\lambda) = {k \over \lambda} \left({x \over \lambda}\right)^{k-1}.$