الرياضيات ، الدوال المثلثية العكسية أو الدوال القوسية (بالإنجليزية : Inverse trigonometric functions ) هي الدوال العكسية للدوال المثلثية معرفة على مجالات محدودة مناسبة معينة.[1] الجيب وجيب التمام والظل وظل التمام والقاطع وقاطع التمام ،
وتستخدم للحصول على زاوية من أي من النسب المثلثية للزاوية. تستخدم الدوال المثلثية العكسية على نطاق واسع في الهندسة التطبيقية والملاحة والفيزياء والهندسة الرياضية .
التدوين [ عدل ] التدوين الأكثر استخدامًا هو تسمية الدوال المثلثية العكسية باستخدام البادئة "arc"، مثل:
arcsin
(
x
)
{\displaystyle \arcsin(x)}
arccos
(
x
)
{\displaystyle \arccos(x)}
arctan
(
x
)
{\displaystyle \arctan(x)}
قوس الجيب ، قوس جيب التمام ... .[2]
أول من استخدم الرموز sin−1 (x ) و cos−1 (x ) هو عالم الرياضيات جون هيرشل . كان ذلك في عام 1813.[3]
غالبًا ما تستخدم تلك التدوينات التي أدخلها جون هيرشل ، وهذا الاتفاق يتوافق مع تدوين دالة عكسية. قد يبدو هذا يتعارض منطقياً مع الدلالات الشائعة لعبارات مثل
sin
2
(
x
)
{\displaystyle \sin ^{2}(x)}
الأُس بدلاً من تركيب الدالة ، وبالتالي قد تؤدي إلى الخلط بين مقلوب العدد والدالة العكسية .
الخصائص الأساسية [ عدل ] القيم الرئيسية [ عدل ] بما أن الدوال المثلثية الست غير متباينة ، تم اقتصارها حتى تكون لها دوال عكسية. لذلك، تكون مديات الدوال العكسية مجموعات فرعية لمديات الدوال الأصلية.
فمثلا، على سبيل المثال، باستخدام الدالة بمعنى الدوال متعددة القيم ، تمامًا كما يمكن تعريف دالة الجذر التربيعي y = √x y 2 = x y = arcsin(x )y ) = x .
إسم
ترميز
تعريف
مجال الدالة
مدى الدالة راديان )
مدى الدالةدرجات )
قوس جيب الزاوية y = arcsin(x ) x = sin (y )
−
1
≤
x
≤
1
{\displaystyle -1\leq x\leq 1}
−
π
2
≤
y
≤
π
2
{\displaystyle -{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}}
−
90
∘
≤
y
≤
90
∘
{\displaystyle -90^{\circ }\leq y\leq 90^{\circ }}
قوس جيب تمام الزاوية y = arccos(x ) x = cos (y )
−
1
≤
x
≤
1
{\displaystyle -1\leq x\leq 1}
0
≤
y
≤
π
{\displaystyle 0\leq y\leq \pi }
0
≤
y
≤
180
∘
{\displaystyle 0\leq y\leq 180^{\circ }}
قوس ظل الزاوية y = arctan(x ) x = tan (y )كل الأعداد الحقيقية (
R
{\displaystyle \mathbb {R} }
−
π
2
<
y
<
π
2
{\displaystyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}}}
−
90
∘
<
y
<
90
∘
{\displaystyle -90^{\circ }<y<90^{\circ }}
قوس ظل تمام الزاوية y = arccot(x ) x = cot (y )كل الأعداد الحقيقية (
R
{\displaystyle \mathbb {R} }
0
<
y
<
π
{\displaystyle 0<y<\pi }
0
<
y
<
180
∘
{\displaystyle 0<y<180^{\circ }}
قوس قاطع الزاوية y = arcsec(x ) x = sec (y )
x
≤
−
1
{\displaystyle x\leq -1}
x
≥
1
{\displaystyle x\geq 1}
0
≤
y
<
π
2
{\displaystyle 0\leq y<{\frac {\pi }{2}}}
π
2
<
y
≤
π
{\displaystyle {\frac {\pi }{2}}<y\leq \pi }
0
≤
y
<
90
∘
{\displaystyle 0\leq y<90^{\circ }}
90
∘
<
y
≤
180
∘
{\displaystyle 90^{\circ }<y\leq 180^{\circ }}
قوس قاطع تمام الزاوية y = arccsc(x ) x = csc (y )
x
≤
−
1
{\displaystyle x\leq -1}
x
≥
1
{\displaystyle x\geq 1}
−
π
2
≤
y
<
0
{\displaystyle -{\frac {\pi }{2}}\leq y<0}
0
<
y
≤
π
2
{\displaystyle 0<y\leq {\frac {\pi }{2}}}
−
90
∘
≤
y
<
0
{\displaystyle -90^{\circ }\leq y<0}
0
<
y
≤
90
∘
{\displaystyle 0<y\leq 90^{\circ }}
العلاقات بين الدوال المثلثية والدوال المثلثية العكسية [ عدل ]
θ
{\displaystyle \theta }
sin
(
θ
)
{\displaystyle \sin(\theta )}
cos
(
θ
)
{\displaystyle \cos(\theta )}
tan
(
θ
)
{\displaystyle \tan(\theta )}
رسم توضيحي
arcsin
(
x
)
{\displaystyle \arcsin(x)}
sin
(
arcsin
(
x
)
)
=
x
{\displaystyle \sin(\arcsin(x))=x}
cos
(
arcsin
(
x
)
)
=
1
−
x
2
{\displaystyle \cos(\arcsin(x))={\sqrt {1-x^{2}}}}
tan
(
arcsin
(
x
)
)
=
x
1
−
x
2
{\displaystyle \tan(\arcsin(x))={\frac {x}{\sqrt {1-x^{2}}}}}
arccos
(
x
)
{\displaystyle \arccos(x)}
sin
(
arccos
(
x
)
)
=
1
−
x
2
{\displaystyle \sin(\arccos(x))={\sqrt {1-x^{2}}}}
cos
(
arccos
(
x
)
)
=
x
{\displaystyle \cos(\arccos(x))=x}
tan
(
arccos
(
x
)
)
=
1
−
x
2
x
{\displaystyle \tan(\arccos(x))={\frac {\sqrt {1-x^{2}}}{x}}}
arctan
(
x
)
{\displaystyle \arctan(x)}
sin
(
arctan
(
x
)
)
=
x
1
+
x
2
{\displaystyle \sin(\arctan(x))={\frac {x}{\sqrt {1+x^{2}}}}}
cos
(
arctan
(
x
)
)
=
1
1
+
x
2
{\displaystyle \cos(\arctan(x))={\frac {1}{\sqrt {1+x^{2}}}}}
tan
(
arctan
(
x
)
)
=
x
{\displaystyle \tan(\arctan(x))=x}
arccsc
(
x
)
{\displaystyle \operatorname {arccsc}(x)}
sin
(
arccsc
(
x
)
)
=
1
x
{\displaystyle \sin(\operatorname {arccsc}(x))={\frac {1}{x}}}
cos
(
arccsc
(
x
)
)
=
x
2
−
1
x
{\displaystyle \cos(\operatorname {arccsc}(x))={\frac {\sqrt {x^{2}-1}}{x}}}
tan
(
arccsc
(
x
)
)
=
1
x
2
−
1
{\displaystyle \tan(\operatorname {arccsc}(x))={\frac {1}{\sqrt {x^{2}-1}}}}
arcsec
(
x
)
{\displaystyle \operatorname {arcsec}(x)}
sin
(
arcsec
(
x
)
)
=
x
2
−
1
x
{\displaystyle \sin(\operatorname {arcsec}(x))={\frac {\sqrt {x^{2}-1}}{x}}}
cos
(
arcsec
(
x
)
)
=
1
x
{\displaystyle \cos(\operatorname {arcsec}(x))={\frac {1}{x}}}
tan
(
arcsec
(
x
)
)
=
x
2
−
1
{\displaystyle \tan(\operatorname {arcsec}(x))={\sqrt {x^{2}-1}}}
arccot
(
x
)
{\displaystyle \operatorname {arccot}(x)}
sin
(
arccot
(
x
)
)
=
1
1
+
x
2
{\displaystyle \sin(\operatorname {arccot}(x))={\frac {1}{\sqrt {1+x^{2}}}}}
cos
(
arccot
(
x
)
)
=
x
1
+
x
2
{\displaystyle \cos(\operatorname {arccot}(x))={\frac {x}{\sqrt {1+x^{2}}}}}
tan
(
arccot
(
x
)
)
=
1
x
{\displaystyle \tan(\operatorname {arccot}(x))={\frac {1}{x}}}
العلاقات بين الدوال المثلثية العكسية [ عدل ] زوايا متتامة:
arccos
(
x
)
=
π
2
−
arcsin
(
x
)
arccot
(
x
)
=
π
2
−
arctan
(
x
)
arccsc
(
x
)
=
π
2
−
arcsec
(
x
)
{\displaystyle {\begin{aligned}\arccos(x)&={\frac {\pi }{2}}-\arcsin(x)\\[0.5em]\operatorname {arccot}(x)&={\frac {\pi }{2}}-\arctan(x)\\[0.5em]\operatorname {arccsc}(x)&={\frac {\pi }{2}}-\operatorname {arcsec}(x)\end{aligned}}}
مداخلها عبارة عن مقابل متغيرها:
arcsin
(
−
x
)
=
−
arcsin
(
x
)
arccos
(
−
x
)
=
π
−
arccos
(
x
)
arctan
(
−
x
)
=
−
arctan
(
x
)
arccot
(
−
x
)
=
π
−
arccot
(
x
)
arcsec
(
−
x
)
=
π
−
arcsec
(
x
)
arccsc
(
−
x
)
=
−
arccsc
(
x
)
{\displaystyle {\begin{aligned}\arcsin(-x)&=-\arcsin(x)\\\arccos(-x)&=\pi -\arccos(x)\\\arctan(-x)&=-\arctan(x)\\\operatorname {arccot}(-x)&=\pi -\operatorname {arccot}(x)\\\operatorname {arcsec}(-x)&=\pi -\operatorname {arcsec}(x)\\\operatorname {arccsc}(-x)&=-\operatorname {arccsc}(x)\end{aligned}}}
مداخلها عبارة عن مقلوب متغيرها:
arccos
(
1
x
)
=
arcsec
(
x
)
arcsin
(
1
x
)
=
arccsc
(
x
)
arctan
(
1
x
)
=
π
2
−
arctan
(
x
)
=
arccot
(
x
)
,
if
x
>
0
arctan
(
1
x
)
=
−
π
2
−
arctan
(
x
)
=
arccot
(
x
)
−
π
,
if
x
<
0
arccot
(
1
x
)
=
π
2
−
arccot
(
x
)
=
arctan
(
x
)
,
if
x
>
0
arccot
(
1
x
)
=
3
π
2
−
arccot
(
x
)
=
π
+
arctan
(
x
)
,
if
x
<
0
arcsec
(
1
x
)
=
arccos
(
x
)
arccsc
(
1
x
)
=
arcsin
(
x
)
{\displaystyle {\begin{aligned}\arccos \left({\frac {1}{x}}\right)&=\operatorname {arcsec}(x)\\[0.3em]\arcsin \left({\frac {1}{x}}\right)&=\operatorname {arccsc}(x)\\[0.3em]\arctan \left({\frac {1}{x}}\right)&={\frac {\pi }{2}}-\arctan(x)=\operatorname {arccot}(x)\,,{\text{ if }}x>0\\[0.3em]\arctan \left({\frac {1}{x}}\right)&=-{\frac {\pi }{2}}-\arctan(x)=\operatorname {arccot}(x)-\pi \,,{\text{ if }}x<0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&={\frac {\pi }{2}}-\operatorname {arccot}(x)=\arctan(x)\,,{\text{ if }}x>0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&={\frac {3\pi }{2}}-\operatorname {arccot}(x)=\pi +\arctan(x)\,,{\text{ if }}x<0\\[0.3em]\operatorname {arcsec} \left({\frac {1}{x}}\right)&=\arccos(x)\\[0.3em]\operatorname {arccsc} \left({\frac {1}{x}}\right)&=\arcsin(x)\end{aligned}}}
المتطابقات [ عدل ] متطابقات المجموع والفرق [ عدل ]
arcsin
α
±
arcsin
β
=
arcsin
(
α
1
−
β
2
±
β
1
−
α
2
)
{\displaystyle \arcsin \alpha \pm \arcsin \beta =\arcsin(\alpha {\sqrt {1-\beta ^{2}}}\pm \beta {\sqrt {1-\alpha ^{2}}})}
arccos
α
±
arccos
β
=
arccos
(
α
β
∓
(
1
−
α
2
)
(
1
−
β
2
)
)
{\displaystyle \arccos \alpha \pm \arccos \beta =\arccos(\alpha \beta \mp {\sqrt {(1-\alpha ^{2})(1-\beta ^{2})}})}
arctan
α
±
arctan
β
=
arctan
(
α
±
β
1
∓
α
β
)
{\displaystyle \arctan \alpha \pm \arctan \beta =\arctan \left({\frac {\alpha \pm \beta }{1\mp \alpha \beta }}\right)}
متطابقات أخرى [ عدل ]
arcsin
(
x
)
+
arccos
(
x
)
=
π
2
{\displaystyle \arcsin(x)+\arccos(x)={\pi \over 2}\;}
arctan
(
x
)
+
arccot
(
x
)
=
π
2
.
{\displaystyle \arctan(x)+\operatorname {arccot}(x)={\pi \over 2}.\;}
arctan
(
x
)
+
arctan
(
1
x
)
=
{
π
2
,
if
x
>
0
−
π
2
,
if
x
<
0
{\displaystyle \arctan(x)+\arctan \left({1 \over x}\right)=\left\{{\begin{matrix}{\pi \over 2},&{\mbox{if }}x>0\\-{\pi \over 2},&{\mbox{if }}x<0\end{matrix}}\right.}
arccos
(
x
)
+
arccos
(
−
x
)
=
π
.
{\displaystyle \arccos(x)+\arccos(-x)=\pi .\;}
arccos
(
x
)
=
arcsin
(
1
−
x
2
)
,
if
0
≤
x
≤
1
arccos
(
x
)
=
1
2
arccos
(
2
x
2
−
1
)
,
if
0
≤
x
≤
1
arcsin
(
x
)
=
1
2
arccos
(
1
−
2
x
2
)
,
if
0
≤
x
≤
1
arcsin
(
x
)
=
arctan
(
x
1
−
x
2
)
arctan
(
x
)
=
arcsin
(
x
1
+
x
2
)
{\displaystyle {\begin{aligned}\arccos(x)&=\arcsin \left({\sqrt {1-x^{2}}}\right)\,,{\text{ if }}0\leq x\leq 1\\\arccos(x)&={\frac {1}{2}}\arccos \left(2x^{2}-1\right)\,,{\text{ if }}0\leq x\leq 1\\\arcsin(x)&={\frac {1}{2}}\arccos \left(1-2x^{2}\right)\,,{\text{ if }}0\leq x\leq 1\\\arcsin(x)&=\arctan \left({\frac {x}{\sqrt {1-x^{2}}}}\right)\\\arctan(x)&=\arcsin \left({\frac {x}{\sqrt {1+x^{2}}}}\right)\end{aligned}}}
اشتقاق وتكامل الدوال المثلثية العكسية [ عدل ] اشتقاقات الدوال المثلثية العكسية [ عدل ] تُبين فيما يلي، اشتقاقات الدوال المثلثية العكسية بالنسبة لقيم عقدية أو حقيقية للمتغير x:
d
d
x
arcsin
x
=
1
1
−
x
2
d
d
x
arccos
x
=
−
1
1
−
x
2
d
d
x
arctan
x
=
1
1
+
x
2
d
d
x
arccot
x
=
−
1
1
+
x
2
d
d
x
arcsec
x
=
1
x
x
2
−
1
d
d
x
arccsc
x
=
−
1
x
x
2
−
1
{\displaystyle {\begin{aligned}{\frac {d}{dx}}\arcsin x&{}={\frac {1}{\sqrt {1-x^{2}}}}\\{\frac {d}{dx}}\arccos x&{}={\frac {-1}{\sqrt {1-x^{2}}}}\\{\frac {d}{dx}}\arctan x&{}={\frac {1}{1+x^{2}}}\\{\frac {d}{dx}}\operatorname {arccot} x&{}={\frac {-1}{1+x^{2}}}\\{\frac {d}{dx}}\operatorname {arcsec} x&{}={\frac {1}{x\,{\sqrt {x^{2}-1}}}}\\{\frac {d}{dx}}\operatorname {arccsc} x&{}={\frac {-1}{x\,{\sqrt {x^{2}-1}}}}\end{aligned}}}
=
المتساويتان التاليتان صالحتان فقط عندما يكون العدد x حقيقيا:
d
d
x
arcsec
x
=
1
|
x
|
x
2
−
1
;
|
x
|
>
1
d
d
x
arccsc
x
=
−
1
|
x
|
x
2
−
1
;
|
x
|
>
1
{\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arcsec} x&{}={\frac {1}{|x|\,{\sqrt {x^{2}-1}}}};\qquad |x|>1\\{\frac {d}{dx}}\operatorname {arccsc} x&{}={\frac {-1}{|x|\,{\sqrt {x^{2}-1}}}};\qquad |x|>1\end{aligned}}}
على سبيل المثال، إذا توفر
θ
=
arcsin
x
{\displaystyle \theta =\arcsin x\!}
d
arcsin
x
d
x
=
d
θ
d
sin
θ
=
d
θ
cos
θ
d
θ
=
1
cos
θ
=
1
1
−
sin
2
θ
=
1
1
−
x
2
{\displaystyle {\frac {d\arcsin x}{dx}}={\frac {d\theta }{d\sin \theta }}={\frac {d\theta }{\cos \theta d\theta }}={\frac {1}{\cos \theta }}={\frac {1}{\sqrt {1-\sin ^{2}\theta }}}={\frac {1}{\sqrt {1-x^{2}}}}}
تكاملات الدوال المثلثية العكسية [ عدل ] باستخدام التكامل بالتجزئة ، نجد أن:
∫
arcsin
(
x
)
d
x
=
x
arcsin
(
x
)
+
1
−
x
2
+
C
∫
arccos
(
x
)
d
x
=
x
arccos
(
x
)
−
1
−
x
2
+
C
∫
arctan
(
x
)
d
x
=
x
arctan
(
x
)
−
1
2
ln
(
1
+
x
2
)
+
C
∫
arccot
(
x
)
d
x
=
x
arccot
(
x
)
+
1
2
ln
(
1
+
x
2
)
+
C
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
ln
(
x
+
x
2
−
1
)
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
ln
(
x
+
x
2
−
1
)
+
C
{\displaystyle {\begin{aligned}\int \arcsin(x)\,dx&{}=x\,\arcsin(x)+{\sqrt {1-x^{2}}}+C\\\int \arccos(x)\,dx&{}=x\,\arccos(x)-{\sqrt {1-x^{2}}}+C\\\int \arctan(x)\,dx&{}=x\,\arctan(x)-{\frac {1}{2}}\ln \left(1+x^{2}\right)+C\\\int \operatorname {arccot}(x)\,dx&{}=x\,\operatorname {arccot}(x)+{\frac {1}{2}}\ln \left(1+x^{2}\right)+C\\\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\end{aligned}}}
المتسلسلات غير المنتهية [ عدل ] يمكننا تعبير عن بعض د.م.ع. بواسطة متسلسلة ماكلورين :
arcsin
(
x
)
=
x
+
(
1
2
)
x
3
3
+
(
1
⋅
3
2
⋅
4
)
x
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
x
7
7
+
⋯
=
∑
n
=
0
∞
(
2
n
−
1
)
!
!
(
2
n
)
!
!
x
2
n
+
1
2
n
+
1
=
∑
n
=
0
∞
(
2
n
)
!
(
2
n
n
!
)
2
x
2
n
+
1
2
n
+
1
{\displaystyle {\begin{aligned}\arcsin(x)&=x+\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}+\cdots \\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {x^{2n+1}}{2n+1}}\\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n)!}{(2^{n}n!)^{2}}}{\frac {x^{2n+1}}{2n+1}}\,\end{aligned}}}
arctan
(
x
)
=
x
−
x
3
3
+
x
5
5
−
x
7
7
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
x
2
n
+
1
2
n
+
1
{\displaystyle \arctan(x)=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{2n+1}}\,}
arccos
(
x
)
=
π
2
−
arcsin
(
x
)
=
π
2
−
x
−
(
1
2
)
x
3
3
−
(
1
⋅
3
2
⋅
4
)
x
5
5
−
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
x
7
7
−
⋯
=
π
2
−
∑
n
=
0
∞
(
2
n
−
1
)
!
!
(
2
n
)
!
!
x
2
n
+
1
2
n
+
1
=
π
2
−
∑
n
=
0
∞
(
2
n
)
!
(
2
n
n
!
)
2
x
2
n
+
1
2
n
+
1
{\displaystyle {\begin{aligned}\arccos(x)&={\frac {\pi }{2}}-\arcsin(x)={\frac {\pi }{2}}-x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}-\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}-\cdots \\[5pt]&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {x^{2n+1}}{2n+1}}\\[5pt]&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{(2^{n}n!)^{2}}}{\frac {x^{2n+1}}{2n+1}}\,\end{aligned}}}
حيث تشير n!! إلى عاملي ثنائي (ميز عن «عاملي مرتين» (n!)! ).
الكسور المستمرة لدالة الظل العكسية [ عدل ] فيما يلي، كسران مستمران معممان يمثلان دالة الظل العكسية. قد يستعملان تعويضا لمتسلسلة القوى للتعبير عن دالة الظل العكسية.
arctan
z
=
z
1
+
(
1
z
)
2
3
−
1
z
2
+
(
3
z
)
2
5
−
3
z
2
+
(
5
z
)
2
7
−
5
z
2
+
(
7
z
)
2
9
−
7
z
2
+
⋱
=
z
1
+
(
1
z
)
2
3
+
(
2
z
)
2
5
+
(
3
z
)
2
7
+
(
4
z
)
2
9
+
⋱
{\displaystyle \arctan z={\cfrac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}+{\cfrac {(3z)^{2}}{5-3z^{2}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}{9-7z^{2}+\ddots }}}}}}}}}}={\cfrac {z}{1+{\cfrac {(1z)^{2}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{\cfrac {(4z)^{2}}{9+\ddots \,}}}}}}}}}}\,}
الشكل اللوغاريتمي للدوال [ عدل ] قد يتم التعبير عن هذه الدوال أيضًا باستخدام اللوغاريتمات العقدية . هذا يمَدِّد مجالاتهما إلى المستوي العقدي (المركّب) بطريقة طبيعية. تشبه هذه التعبيرات العبارات اللوغاريتمية للدوال الزائدية العكسية .
arcsin
(
z
)
=
−
i
ln
(
i
z
+
1
−
z
2
)
=
arccsc
(
1
z
)
arccos
(
z
)
=
−
i
ln
(
z
+
z
2
−
1
)
=
π
2
+
i
ln
(
i
z
+
1
−
z
2
)
=
π
2
−
arcsin
(
z
)
=
arcsec
(
1
z
)
arctan
(
z
)
=
i
2
ln
(
i
+
z
i
−
z
)
=
i
2
[
ln
(
1
−
i
z
)
−
ln
(
1
+
i
z
)
]
=
arccot
(
1
z
)
arccot
(
z
)
=
i
2
ln
(
z
−
i
z
+
i
)
=
i
2
[
ln
(
1
−
i
z
)
−
ln
(
1
+
i
z
)
]
=
arctan
(
1
z
)
arcsec
(
z
)
=
−
i
ln
(
1
z
2
−
1
+
1
z
)
=
i
ln
(
1
−
1
z
2
+
i
z
)
+
π
2
=
π
2
−
arccsc
(
z
)
=
arccos
(
1
z
)
arccsc
(
z
)
=
−
i
ln
(
1
−
1
z
2
+
i
z
)
=
arcsin
(
1
z
)
{\displaystyle {\begin{aligned}\arcsin(z)&{}=-i\ln \left(iz+{\sqrt {1-z^{2}}}\right)&{}=\operatorname {arccsc} \left({\frac {1}{z}}\right)\\[10pt]\arccos(z)&{}=-i\ln \left(z+{\sqrt {z^{2}-1}}\right)={\frac {\pi }{2}}\,+i\ln \left(iz+{\sqrt {1-z^{2}}}\right)={\frac {\pi }{2}}-\arcsin(z)&{}=\operatorname {arcsec} \left({\frac {1}{z}}\right)\\[10pt]\arctan(z)&{}={\frac {i}{2}}\ln \left({\frac {i+z}{i-z}}\right)={\frac {i}{2}}\left[\ln(1-iz)-\ln(1+iz)\right]&{}=\operatorname {arccot} \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccot}(z)&{}={\frac {i}{2}}\ln \left({\frac {z-i}{z+i}}\right)={\frac {i}{2}}\left[\ln \left(1-{\frac {i}{z}}\right)-\ln \left(1+{\frac {i}{z}}\right)\right]&{}=\arctan \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arcsec}(z)&{}=-i\ln \left({\sqrt {{\frac {1}{z^{2}}}-1}}+{\frac {1}{z}}\right)=i\,\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)+{\frac {\pi }{2}}={\frac {\pi }{2}}-\operatorname {arccsc}(z)&{}=\arccos \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccsc}(z)&{}=-i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)&{}=\arcsin \left({\frac {1}{z}}\right)\end{aligned}}}
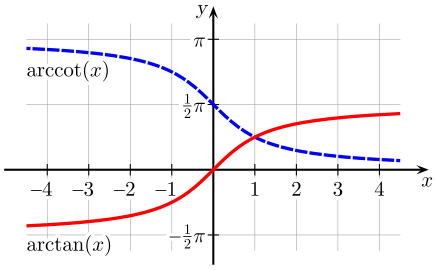
التمثيلات البيانية للدوال [ عدل ] التمثيلات البيانية للدوال في المَعْلَم الديكارتي.
ت.ب لدالتي قوس الجيب (بالأحمر) وقوس جيب التمام (بالأزرق)
ت.ب لدالتي قوس الظل (بالأحمر) وقوس ظل التمام (بالأزرق)
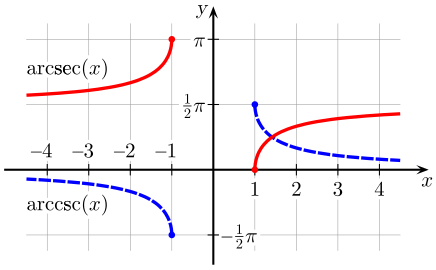
ت.ب لدالتي قوس القاطع (بالأحمر) وقوس قاطع التمام (بالأزرق)
انظر أيضًا [ عدل ] مراجع [ عدل ]
^ "معلومات عن الدوال المثلثية العكسية على موقع mathworld.wolfram.com" . mathworld.wolfram.com. مؤرشف من الأصل في 2019-03-25.^ ميشال إبراهيم ورامي أبو سليمان وفادي (1 يناير 2007). Dictionaire des termes scientifiques (Anglais/Français/Arabe): قاموس المصطلحات العلمية - انكليزي/فرنسي/عربي ISBN :978-2-7451-5445-3 الأصل في 2020-02-20. ^ Graham Hall et Fred Goodrich Frink, chap. II « The Acute Angle (14) Inverse trigonometric functions », dans Trigonometry, Ann Arbor, Michigan, USA, Henry Holt and Company / Norwood Press / J. S. Cushing Co. - Berwick & Smith Co., Norwood, Massachusetts, USA, janvier 1909 ,I: Plane Trigonometry, p. 15.. نسخة محفوظة 5 يوليو 2019 على موقع واي باك مشين .

























































![{\displaystyle {\begin{aligned}\arccos(x)&={\frac {\pi }{2}}-\arcsin(x)\\[0.5em]\operatorname {arccot}(x)&={\frac {\pi }{2}}-\arctan(x)\\[0.5em]\operatorname {arccsc}(x)&={\frac {\pi }{2}}-\operatorname {arcsec}(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec43798232f580abb074cf15f3d77692edd36af0)

![{\displaystyle {\begin{aligned}\arccos \left({\frac {1}{x}}\right)&=\operatorname {arcsec}(x)\\[0.3em]\arcsin \left({\frac {1}{x}}\right)&=\operatorname {arccsc}(x)\\[0.3em]\arctan \left({\frac {1}{x}}\right)&={\frac {\pi }{2}}-\arctan(x)=\operatorname {arccot}(x)\,,{\text{ if }}x>0\\[0.3em]\arctan \left({\frac {1}{x}}\right)&=-{\frac {\pi }{2}}-\arctan(x)=\operatorname {arccot}(x)-\pi \,,{\text{ if }}x<0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&={\frac {\pi }{2}}-\operatorname {arccot}(x)=\arctan(x)\,,{\text{ if }}x>0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&={\frac {3\pi }{2}}-\operatorname {arccot}(x)=\pi +\arctan(x)\,,{\text{ if }}x<0\\[0.3em]\operatorname {arcsec} \left({\frac {1}{x}}\right)&=\arccos(x)\\[0.3em]\operatorname {arccsc} \left({\frac {1}{x}}\right)&=\arcsin(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecb0a376d9148e3cf65ea6e6ed5fb37752a581c7)













![{\displaystyle {\begin{aligned}\arcsin(x)&=x+\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}+\cdots \\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {x^{2n+1}}{2n+1}}\\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n)!}{(2^{n}n!)^{2}}}{\frac {x^{2n+1}}{2n+1}}\,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92b62bf5b37765271c47e9788914ff0efdc965a2)

![{\displaystyle {\begin{aligned}\arccos(x)&={\frac {\pi }{2}}-\arcsin(x)={\frac {\pi }{2}}-x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}-\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}-\cdots \\[5pt]&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {x^{2n+1}}{2n+1}}\\[5pt]&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{(2^{n}n!)^{2}}}{\frac {x^{2n+1}}{2n+1}}\,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ffbad34ed3a8e64858c108533407e7a0a0551c6)

![{\displaystyle {\begin{aligned}\arcsin(z)&{}=-i\ln \left(iz+{\sqrt {1-z^{2}}}\right)&{}=\operatorname {arccsc} \left({\frac {1}{z}}\right)\\[10pt]\arccos(z)&{}=-i\ln \left(z+{\sqrt {z^{2}-1}}\right)={\frac {\pi }{2}}\,+i\ln \left(iz+{\sqrt {1-z^{2}}}\right)={\frac {\pi }{2}}-\arcsin(z)&{}=\operatorname {arcsec} \left({\frac {1}{z}}\right)\\[10pt]\arctan(z)&{}={\frac {i}{2}}\ln \left({\frac {i+z}{i-z}}\right)={\frac {i}{2}}\left[\ln(1-iz)-\ln(1+iz)\right]&{}=\operatorname {arccot} \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccot}(z)&{}={\frac {i}{2}}\ln \left({\frac {z-i}{z+i}}\right)={\frac {i}{2}}\left[\ln \left(1-{\frac {i}{z}}\right)-\ln \left(1+{\frac {i}{z}}\right)\right]&{}=\arctan \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arcsec}(z)&{}=-i\ln \left({\sqrt {{\frac {1}{z^{2}}}-1}}+{\frac {1}{z}}\right)=i\,\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)+{\frac {\pi }{2}}={\frac {\pi }{2}}-\operatorname {arccsc}(z)&{}=\arccos \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccsc}(z)&{}=-i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)&{}=\arcsin \left({\frac {1}{z}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7621fcfe397c23cf51412c21812c2be167565eb0)