نسبة ذهبية

شرائح الخط في النسبة الذهبية

المستطيل الذهبي ذو الضلع الطويل أ والجانب القصير ب المجاور لمربع بجوانب طولها أ ينتج عنه مستطيل ذهبي مشابه له ضلع طويل أ + ب وضلع قصير أ . هذا يوضح العلاقة ${\frac {a+b}{a}}={\frac {a}{b}}\equiv \varphi$

${\frac {a+b}{a}}={\frac {a}{b}}\equiv \varphi$

النسبة الذهبية (بالإنجليزية: Golden Ratio)‏ في الرياضيات تحقق عندما يكون مجموع عددين مقسوم على أكبرهما يساوي خارج قسمة أكبر العددين على أصغرهما، أي أنه توجد كميتان في النسبة الذهبية إذا كانت نسبتهما هي نفس نسبة مجموعهما إلى أكبر الكميتين. يوضح الشكل الموجود على اليمين العلاقة الهندسية. فإذا كان a أكبر من b فإن النسبة الذهبية جبرياً هي تحقق:

${\frac {a+b}{a}}={\frac {a}{b}}\ {\stackrel {\text{def}}{=}}\ \varphi ,$

حيث الحرف اليوناني phi ( $\varphi$ أو $\phi$ ) يمثل النسبة الذهبية. هو رقم غير نسبي يمثل حلًا للمعادلة التربيعية $x^{2}-x-1=0$ بقيمة:

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.6180339887\ldots .$

وهو ثابت رياضي معرف تبلغ قيمته 1.6180339887 تقريبا.

لو نُظر إلى مستطيلات مختلفة، لوُجد بعضها أجمل من الآخر. وفي معظم الأحيان تكون نسبة أبعاد هذه المستطيلات بعضها إلى بعض هي نفسها. وتسمى هذه المستطيلات "المستطيلات الذهبية" وخارج قسمة طولها على عرضها يسمى "الرقم الذهبي".

طريقة إنشاء المستطيل الذهبي. المربع مبين باللون الأحمر

فنجد أنه في المستطيل الذهبي نسبة الطول إلى العرض تساوي $\varphi$.

وجرت العادة أن يكتب الرقم الذهبي باعتماد الحرف الاغريقي Φ "يُنطق فاي أو في" أو رياضيا $\varphi$. وقد ظهرت هذه التسمية سنة 1914 وفاء لذكرى "فيدياس"، وهو نحّات قام بتزيين "البارثينون" في أثينا.

ويظهر الرقم الذهبي أيضا في أشكال هندسية أخرى منها خماسي الأضلاع المنتظم، وهو شكل هندسي ذو خمس أضلاع محتوى في دائرة، و أضلاعه وزواياه كلها متقايسة. وفي هذا الشكل يمثل خارج قسمة القطر على أحد الأضلاع الرقم الذهبي وهو عرضة للتشكيك في كثير من الأحيان من حيث أن أرقام مشابهة تكون موجودة ويتم الترويج إلى أن الرقم موجود بذاته أو أن الرقم لا يكون موجوداً في حالات كثيرة ويُدعى أنه موجود.

تسمى النسبة الذهبية أيضًا بالمتوسط الذهبي أو القسم الذهبي ( لاتيني : مقطع aurea ). وتشمل أسماء أخرى متطرفة ونسبة متوسط، قسم وسطي، نسبة الإلهية (اللاتينية: الإلهية proportio)، القسم الإلهي (اللاتينية: الإلهية التقطيعة)، نسبة الذهبية، وقطع ذهبية، ورقم ذهبي .

درس علماء الرياضيات منذ إقليدس خصائص النسبة الذهبية ، بما في ذلك مظهرها في أبعاد البنتاغون العادي وفي المستطيل الذهبي ، والتي يمكن تقطيعها إلى مربع ومستطيل أصغر بنفس نسبة العرض إلى الارتفاع . تم استخدام النسبة الذهبية أيضًا لتحليل نسب الأشياء الطبيعية وكذلك الأنظمة التي من صنع الإنسان مثل الأسواق المالية ، في بعض الحالات بناءً على نوبات مشكوك فيها للبيانات. تظهر النسبة الذهبية في بعض الأنماط في الطبيعة ، بما في ذلك الترتيب الحلزوني للأوراق وأجزاء النبات الأخرى.

قام بعض الفنانين والمهندسين المعماريين في القرن العشرين ، بما في ذلك لو كوربوزييه وسلفادور دالي ، بتناسب أعمالهم لتقريب النسبة الذهبية ، معتقدين أن هذا ممتع من الناحية الجمالية . غالبًا ما تظهر هذه في شكل مستطيل ذهبي ، حيث تكون نسبة الجانب الأطول إلى الأقصر هي النسبة الذهبية.

عملية حسابية

قائمة الأعداد أعداد غير كسرية γ ζ(3) √2 √3 √5 φ ρ δS e π δ
الثنائية	1.1001111000110111011. . .
عدد عشري	1.6180339887498948482. . .
السداسي عشري	1.9E3779B97F4A7C15F39. . .
جزء مستمر	$1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}}$
شكل جبري	${\frac {1+{\sqrt {5}}}{2}}$

يُقال إن الكميتين أ و ب في النسبة الذهبية φ إذا

${\frac {a+b}{a}}={\frac {a}{b}}=\varphi .$

إحدى طرق إيجاد قيمة φ هي البدء بالكسر الأيسر. من خلال تبسيط الكسر والتعويض في ب / أ = 1 / φ ،

${\frac {a+b}{a}}={\frac {a}{a}}+{\frac {b}{a}}=1+{\frac {b}{a}}=1+{\frac {1}{\varphi }}.$

وبالتالي،

$1+{\frac {1}{\varphi }}=\varphi .$

الضرب في φ يعطي

$\varphi +1=\varphi ^{2}$

الذي يمكن إعادة ترتيبه إلى

${\varphi }^{2}-\varphi -1=0.$

باستخدام الصيغة التربيعية ، يتم الحصول على حلين:

${\frac {1+{\sqrt {5}}}{2}}=1.618\,033\,988\,7\dots$ و ${\frac {1-{\sqrt {5}}}{2}}=-0.618\,033\,988\,7\dots$

لأن φ هي النسبة بين الكميات الموجبة ، φ موجبة بالضرورة:

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.61803\,39887\dots$

قائمة الأعداد أعداد غير كسرية γ ζ(3) √2 √3 √5 φ ρ δS e π δ
الثنائية	1.1001111000110111011. . .
عدد عشري	1.6180339887498948482. . .
السداسي عشري	1.9E3779B97F4A7C15F39. . .
جزء مستمر	$1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}}$
شكل جبري	${\frac {1+{\sqrt {5}}}{2}}$

التاريخ

«Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties. ... Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.»

وفقًا لماريو ليفيو، درس علماء الرياضيات اليونانيون القدماء لأول مرة ما نسميه الآن النسبة الذهبية ، بسبب ظهورها المتكرر في الهندسة . تقسيم الخط إلى "نسبة متطرفة ومتوسطة" (القسم الذهبي) مهم في هندسة الخماسيات والخماسيات المنتظمة. وفقًا لقصة واحدة ، اكتشف عالم الرياضيات هيباسوس من القرن الخامس قبل الميلاد أن النسبة الذهبية لم تكن عددًا صحيحًا ولا جزءًا ( عددًا غير نسبي ) ، مما أثار دهشة الفيثاغورس . عناصر إقليدس ( c. 300 BC ) تقدم العديد من الافتراضات وإثباتاتها باستخدام النسبة الذهبية ، وتحتوي على أول تعريف معروف لها والذي يستمر على النحو التالي:

«A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.»

تمت دراسة النسبة الذهبية محيطيًا خلال الألفية التالية. استخدمها أبو كامل (حوالي 850-930) في حساباته الهندسية للخماسيات والعشاري. أثرت كتاباته على كتابات فيبوناتشي (ليوناردو بيزا) (1170-1250) ، الذي استخدم النسبة في مسائل الهندسة ذات الصلة ، على الرغم من عدم ربطها مطلقًا بسلسلة الأرقام التي سميت باسمه .

أطلق لوكا باسيولي على كتابه نسبة Divina ( 1509 ) بعد النسبة ، واستكشف خصائصه بما في ذلك ظهوره في بعض المواد الصلبة الأفلاطونية . أطلق ليوناردو دافنشي ، الذي رسم الكتاب المذكور أعلاه ، على نسبة المقطع aurea ("القسم الذهبي"). حل علماء الرياضيات في القرن السادس عشر مثل رافائيل بومبيلي المسائل الهندسية باستخدام النسبة.

German mathematician Simon Jacob (d. 1564) noted that consecutive Fibonacci numbers converge to the golden ratio; this was rediscovered by Johannes Kepler in 1608. The first known decimal approximation of the (inverse) golden ratio was stated as "about 0.6180340" in 1597 by Michael Maestlin of the University of Tübingen in a letter to Kepler, his former student. The same year, Kepler wrote to Maestlin of the Kepler triangle, which combines the golden ratio with the Pythagorean theorem. Kepler said of these:

«Geometry has two great treasures: one is the theorem of Pythagoras, the other the division of a line into extreme and mean ratio. The first we may compare to a mass of gold, the second we may call a precious jewel.»

استخدم علماء الرياضيات في القرن الثامن عشر أبراهام دي موفر ودانييل برنولي وليونهارد أويلر صيغة قائمة على النسبة الذهبية والتي تجد قيمة رقم فيبوناتشي بناءً على موضعه في التسلسل ؛ في عام 1843 ، تم اكتشاف هذا بواسطة جاك فيليب ماري بينيه ، الذي أطلق عليه اسم "صيغة بينيه". استخدم مارتن أوم لأول مرة المصطلح الألماني goldener Schnitt ("القسم الذهبي") لوصف النسبة في عام 1835. استخدم جيمس سولي المصطلح الإنجليزي المكافئ في عام 1875.

بحلول عام 1910 ، بدأ عالم الرياضيات مارك بار في استخدام الحرف اليوناني فاي ( φ ) كرمز للنسبة الذهبية. تم تمثيله أيضًا بواسطة tau ( τ ) ، الحرف الأول من اليونانية القديمة τομή ("قص" أو "قسم").

بين عامي 1973 و 1974 ، طور روجر بنروز تبليط بنروز ، وهو نمط مرتبط بالنسبة الذهبية في كل من نسبة مساحات بلاطيتيها المعينية وترددها النسبي داخل النموذج. أدى هذا إلى اكتشاف دان شيختمان في أوائل ثمانينيات القرن الماضي لأشباه البلورات ، والتي يُظهر بعضها تناظرًا عشريًا الوجوه .

التطبيقات والملاحظات

هندسة معمارية

المئذنة كما تُرى من باحة الجامع الكبير بالقيروان

كشف تحليل هندسي أجري عام 2004 لبحث سابق في الجامع الكبير بالقيروان (670) عن تطبيق النسبة الذهبية في كثير من التصميم. ووجدوا نسبًا قريبة من النسبة الذهبية في الشكل العام وفي أبعاد مكان الصلاة والفناء والمئذنة . ومع ذلك ، فإن المناطق ذات النسب القريبة من النسبة الذهبية لم تكن جزءًا من الخطة الأصلية ، ومن المحتمل أنها تمت إضافتها في إعادة الإعمار.

تم التكهن باستخدام النسبة الذهبية من قبل مصممي ساحة نقش جهان (1629) ومسجد لطف الله المجاور.

ركز المهندس المعماري السويسري لو كوربوزييه ، المشهور بإسهاماته في الأسلوب الدولي الحديث ، فلسفته في التصميم على أنظمة التناغم والتناسب. ارتبط إيمان لو كوربوزييه بالترتيب الرياضي للكون ارتباطًا وثيقًا بالنسبة الذهبية وسلسلة فيبوناتشي ، التي وصفها بأنها "إيقاعات واضحة للعين وواضحة في علاقاتها مع بعضها البعض. وهذه الإيقاعات هي أصل الأنشطة البشرية. إنهم يترددون في الإنسان بحتمية عضوية ، نفس الحتمية الدقيقة التي تسبب اقتفاء أثر القسم الذهبي من قبل الأطفال والشيوخ والمتوحشين والمتعلمين. "

استخدم لو كوربوزييه صراحة النسبة الذهبية في نظام Modulor الخاص به لمقياس النسبة المعمارية . لقد رأى هذا النظام باعتباره استمرارًا للتقليد الطويل لفيتروفيوس ، و " فيتروفيان مان " لليوناردو دافنشي ، وعمل ليون باتيستا ألبيرتي ، وغيرهم ممن استخدموا نسب جسم الإنسان لتحسين مظهر ووظيفة العمارة .

بالإضافة إلى النسبة الذهبية ، بنى لو كوربوزييه النظام على القياسات البشرية وأرقام فيبوناتشي والوحدة المزدوجة. لقد أخذ اقتراح النسبة الذهبية في النسب البشرية إلى أقصى الحدود: لقد قسّم نموذجه لجسم الإنسان عند السرة مع قسمين في نسبة ذهبية ، ثم قسّم هذه المقاطع بنسبة ذهبية عند الركبتين والحلق ؛ استخدم نسب النسبة الذهبية هذه في نظام Modulor . مثال على فيلا شتاين لو كوربوزييه عام 1927 في Garches تطبيق نظام Modulor. المخطط الأرضي المستطيل للفيلا والارتفاع والبنية الداخلية قريبة من المستطيلات الذهبية.

أسس مهندس معماري سويسري آخر ، ماريو بوتا ، العديد من تصميماته على أشكال هندسية. تتكون العديد من المنازل الخاصة التي صممها في سويسرا من مربعات ودوائر ومكعبات وأسطوانات. في المنزل الذي صممه في Origlio ، النسبة الذهبية هي النسبة بين القسم المركزي والأقسام الجانبية للمنزل.

فن

رسم ليوناردو للعنصر ثنائي الوجوه من Pacioli 's Divina ratioe (1509)

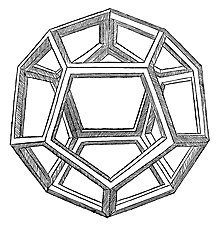
تم نشر Divina نسبة ( النسبة الإلهية ) ، وهو عمل مكون من ثلاثة مجلدات بواسطة Luca Pacioli ، في عام 1509. كان الراهب الفرنسيسكاني باسيولي معروفًا في الغالب بكونه عالم رياضيات ، لكنه أيضًا كان مدربًا ومهتمًا للغاية بالفن. استكشفت Divina ratioe رياضيات النسبة الذهبية. على الرغم من أنه كثيرًا ما يُقال إن باسيولي دعا إلى تطبيق النسبة الذهبية لإعطاء نسب متناغمة ومرضية ، إلا أن ليفيو يشير إلى أن التفسير قد تم تتبعه إلى خطأ في عام 1799 ، وأن باسيولي قد دافع بالفعل عن نظام فيتروفيان للنسب العقلانية. رأى باسيولي أيضًا أهمية دينية كاثوليكية في النسبة ، مما أدى إلى عنوان عمله.

أدت الرسوم التوضيحية لليوناردو دافنشي عن متعدد السطوح في Divina ratioe إلى التكهن بأنه قد أدرج النسبة الذهبية في لوحاته. لكن الإيحاء بأن لوحة الموناليزا الخاصة به ، على سبيل المثال ، تستخدم نسب النسبة الذهبية ، لا تدعمها كتابات ليوناردو. وبالمثل ، على الرغم من أن الرجل فيتروفيان يظهر غالبًا فيما يتعلق بالنسبة الذهبية ، إلا أن نسب الشكل لا تتطابق معها في الواقع ، ويذكر النص فقط نسب الأعداد الصحيحة.

استخدم سلفادور دالي ، متأثرًا بأعمال ماتيلا غيكا ، بوضوح النسبة الذهبية في تحفته ، سر العشاء الأخير . أبعاد اللوحة عبارة عن مستطيل ذهبي. يتدلى من اثنا عشر وجهًا ضخمًا ، في المنظور بحيث تظهر الحواف بنسبة ذهبية لبعضها البعض ، فوق وخلف يسوع ويسيطر على التكوين.

وجدت دراسة إحصائية أجريت عام 1999 على 565 عملاً فنياً لرسامين عظماء مختلفين أن هؤلاء الفنانين لم يستخدموا النسبة الذهبية في حجم لوحاتهم. وخلصت الدراسة إلى أن متوسط نسبة جانبي اللوحات المدروسة 1.34 بمتوسطات للفنانين الفرديين تتراوح من 1.04 (جويا) إلى 1.46 (بيليني). من ناحية أخرى ، أدرج Pablo Tosto أكثر من 350 عملاً لفنانين مشهورين ، بما في ذلك أكثر من 100 من اللوحات ذات المستطيل الذهبي ونسب الجذر 5 ، وأخرى بنسب مثل root-2 و 3 و 4 و 6.

تصوير النسب في مخطوطة من العصور الوسطى. وفقًا لـ Jan Tschichold : "نسبة الصفحة 2: 3. نسب الهامش 1: 1: 2: 3. تتناسب منطقة النص في القسم الذهبي ".

الكتب والتصميم

وفقًا لـ Jan Tschichold ، كان هناك وقت كانت فيه الانحرافات عن نسب الصفحات الجميلة حقًا 2: 3 ، 1: 3 ، والقسم الذهبي كانت نادرة. تظهر العديد من الكتب التي تم إنتاجها بين عامي 1550 و 1770 هذه النسب بالضبط ، في حدود نصف ملليمتر.

ووفقًا لبعض المصادر ، يتم استخدام النسبة الذهبية في التصميم اليومي ، على سبيل المثال في نسب أوراق اللعب ، والبطاقات البريدية ، والملصقات ، ولوحات الإضاءة ، وأجهزة التلفزيون ذات الشاشة العريضة.

موسيقى

يحلل Ernő Lendvai أعمال Béla Bartók على أنها تستند إلى نظامين متعارضين ، نظام النسبة الذهبية والمقياس الصوتي ، الرغم من رفض علماء الموسيقى الآخرين لهذا التحليل. استخدم الملحن الفرنسي إريك ساتي النسبة الذهبية في العديد من مقطوعاته ، بما في ذلك Sonneries de la Rose + Croix . تظهر النسبة الذهبية أيضًا في تنظيم المقاطع في موسيقى Reflets dans l'eau (انعكاسات في الماء) لديبوسي ، من الصور (السلسلة الأولى ، 1905) ، حيث "يتم تمييز تسلسل المفاتيح بواسطة الفترات 34 و 21 و 13 و 8 ، والذروة الرئيسية تجلس في موقع فاي ".

لاحظ عالم الموسيقى Roy Howat أن الحدود الرسمية لـ Debussy's La Mer تتوافق تمامًا مع القسم الذهبي. يجد Trezise أن الدليل الجوهري "رائع" ، لكنه يحذر من أنه لا يوجد دليل مكتوب أو معلن يشير إلى أن ديبوسي سعى بوعي إلى مثل هذه النسب.

تضع Pearl Drums فتحات التهوية في طرازات Masters Premium بناءً على النسبة الذهبية. تدعي الشركة أن هذا الترتيب يحسن استجابة الجهير وقد تقدمت بطلب للحصول على براءة اختراع لهذا الابتكار.

على الرغم من أن Heinz Bohlen اقترح مقياس 833 سنتًا غير مكرر للأوكتاف استنادًا إلى النغمات المركبة ، فإن الضبط يتميز بالعلاقات القائمة على النسبة الذهبية. كفترة موسيقية ، النسبة 1.618 ... هي 833.090 ... سنتًا ( Play^ⓘ</img> Play^ⓘ).

طبيعة

تفاصيل نبات الصحن ، Aeonium tabuliforme ، يُظهر الترتيب اللولبي المتعدد ( parastichy )

كتب يوهانس كيبلر أن "صورة الرجل والمرأة تنبع من النسبة الإلهية. في رأيي ، تكاثر النباتات والأفعال التكاثرية للحيوانات في نفس النسبة".

لاحظ عالم النفس Adolf Zeising أن النسبة الذهبية ظهرت في phyllotaxis وجادل من هذه الأنماط في الطبيعة أن النسبة الذهبية هي قانون عالمي. كتب زيزينج في عام 1854 عن قانون تقويم العظام الشامل " للسعي من أجل الجمال والاكتمال في مجالات الطبيعة والفن".

في عام 2010 ، ذكرت مجلة Science أن النسبة الذهبية موجودة على المقياس الذري في الرنين المغناطيسي للسبينات في بلورات الكوبالت النيوبيتية.

ومع ذلك ، فقد جادل البعض بأن العديد من المظاهر الواضحة للنسبة الذهبية في الطبيعة ، خاصة فيما يتعلق بأبعاد الحيوانات ، وهمية.

تحسين

النسبة الذهبية هي مفتاح البحث في golden-section (المقطع الذهبي) .

الرياضيات

اللاعقلانية

النسبة الذهبية هي رقم غير نسبي. فيما يلي دليلان قصيران على اللاعقلانية:

تناقض من تعبير بأدنى حد

إذا كانت φ العقلاني ، فإنه سيكون من نسبة جانبي مستطيل مع الجانبين صحيح (المستطيل يضم المخطط بأكمله). لكنها ستكون أيضًا نسبة جوانب عدد صحيح للمستطيل الأصغر (الجزء الأيمن من الرسم التخطيطي) يتم الحصول عليها بحذف مربع. تسلسل تناقص أطوال أضلاع الأعداد الصحيحة المتكونة من حذف المربعات لا يمكن أن يستمر إلى ما لا نهاية لأن الأعداد الصحيحة لها حد أدنى ، لذلك لا يمكن أن تكون φ منطقية.

تذكر أن:

الكل هو الجزء الأطول بالإضافة إلى الجزء الأقصر ؛

الكل هو الجزء الأطول حيث أن الجزء الأطول هو الجزء الأقصر.

إذا استدعينا n بالكامل والجزء الأطول m ، فإن العبارة الثانية أعلاه تصبح

n هو m كما m هو n − m

أو جبريًا

${\frac {n}{m}}={\frac {m}{n-m}}.\qquad (*)$

إن القول بأن النسبة الذهبية φ منطقية يعني أن φ كسر n / m حيث n و m عددان صحيحان. قد نأخذ n / m في أدنى حد و n و m موجبين. ولكن إذا كانت n / m بأدنى حد ، فإن الهوية المسمى (*) أعلاه تقول m / ( n - م ) بعبارات أقل. هذا تناقض يتبع من افتراض أن φ عقلاني.

بواسطة اللاعقلانية √5

دليل قصير آخر - ربما يكون أكثر شيوعًا - على لاعقلانية النسبة الذهبية يستخدم إغلاق الأعداد المنطقية تحت عمليات الجمع والضرب. إذا $\textstyle {\frac {1+{\sqrt {5}}}{2}}$ عقلاني ، إذن $\textstyle 2\left({\frac {1+{\sqrt {5}}}{2}}\right)-1={\sqrt {5}}$ هو أيضًا عقلاني ، وهو تناقض إذا كان معروفًا بالفعل أن الجذر التربيعي لعدد طبيعي غير مربع هو غير منطقي.

كثير الحدود الصغرى

النسبة الذهبية هي أيضًا رقم جبري وحتى عدد صحيح جبري . لديها الحد الأدنى من كثير الحدود

$x^{2}-x-1.$

بالحصول على الدرجة 2 ، فإن كثير الحدود هذا له في الواقع جذران ، والآخر هو اقتران النسبة الذهبية.

اقتران النسبة الذهبية

الجذر المترافق مع الحد الأدنى من كثير الحدود x ² - x - 1 هو

$-{\frac {1}{\varphi }}=1-\varphi ={\frac {1-{\sqrt {5}}}{2}}=-0.61803\,39887\dots .$

تتوافق القيمة المطلقة لهذه الكمية (≈ 0.618) مع نسبة الطول المأخوذة بترتيب عكسي (طول مقطع أقصر على طول مقطع أطول ، ب / أ ) ، ويشار إليها أحيانًا باسم النسبة الذهبية المترافقة أو نسبة الفضة . يُشار إليه هنا بالحرف Phi ( $\Phi$ ):

$\Phi ={1 \over \varphi }=\varphi ^{-1}=0.61803\,39887\ldots .$

بدلا من ذلك، $\Phi$ يمكن التعبير عنها كـ

$\Phi =\varphi -1=1.61803\,39887\ldots -1=0.61803\,39887\ldots .$

يوضح هذا الخاصية الفريدة للنسبة الذهبية بين الأرقام الموجبة ، أي

${1 \over \varphi }=\varphi -1,$

أو معكوسه:

${1 \over \Phi }=\Phi +1.$

هذا يعني 0.61803 ...: 1 = 1: 1.61803. . . .

أشكال بديلة

التقريب للنسبة الذهبية المتبادلة بواسطة كسور محدودة مستمرة ، أو نسب أرقام فيبوناتشي

صيغة φ = 1 + 1 / φ يمكن توسيعها بشكل متكرر للحصول على جزء المستمر للالنسبة الذهبية:

$\varphi =[1;1,1,1,\dots ]=1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}$

ومتبادله:

$\varphi ^{-1}=[0;1,1,1,\dots ]=0+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}$

تقاربات هذه الكسور المستمرة (1/1 ، 2/1 ، 3/2 ، 5/3 ، 8/5 ، 13/8 ، ... أو 1/1 ، 1/2 ، 2/3 ، 3 / 5 ، 5/8 ، 8/13 ، ...) هي نسب لأرقام فيبوناتشي المتتالية.

φ المعادلة ² = 1 + φ تنتج أيضا من استمرار الجذر التربيعي :

$\varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\cdots }}}}}}}}.$

يمكن اشتقاق سلسلة لا نهائية للتعبير عن φ :

$\varphi ={\frac {13}{8}}+\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}(2n+1)!}{4^{2n+3}n!(n+2)!}}.$ أيضا:

$\varphi =1+2\sin(\pi /10)=1+2\sin 18^{\circ }$

$\varphi ={1 \over 2}\csc(\pi /10)={1 \over 2}\csc 18^{\circ }$

$\varphi =2\cos(\pi /5)=2\cos 36^{\circ }$

$\varphi =2\sin(3\pi /10)=2\sin 54^{\circ }.$

تتوافق هذه مع حقيقة أن طول قطر الخماسي المنتظم يساوي φ ضعف طول ضلعها ، وعلاقات مماثلة في الخماسي .

قيمته العددية

قيمة الرقم الذهبي الدقيقة هي $\varphi ={\frac {1+{\sqrt {5}}}{2}}$ كما يمكن إثبات أنّ قيمتها $2\cos(36^{\circ })\,$ أيضا ولإيجاد قيمة تقريبية لهذا الرقم يمكننا استعمال آلة حاسبة. قيمة $\varphi$ التقريبية هي 1.618 ولكن عدد الأرقام العشرية لا متناهية ولا يمكن توقّعها أو التكهن بها.

ويمكننا أيضا اعتماد متوالية أو "سلسلة فيبوناتشي" للاقتراب من الرقم الذهبي، وقد تم وضع هذه المتوالية في العصر الوسيط على يد عالم الرياضيات الإيطالي ليوناردو دا بيزّا (نسبة إلى بيزّا المدينة الإيطالية) المسمّى "فيبوناتشي"، لدراسة تكاثر الأرانب.

وأول رقمين في هذه السلسلة هما 1. ولإيجاد مختلف عناصرها، نجمع العنصرين السابقين. فنحصل بالتالي على السلسلة التالية :

و بقسمة كل عنصر على سابقه (بداية من الـ1 الثاني)، نقترب شيئا فشيئاً من الرقم الذهبي

و في النهاية، يمكننا اعتماد هذا الكسر المستمر لإيجاد قيمة قريبة من قيمة φ:

$\varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\cdots }}}}}}}}.$

الاستفادة منه

صورة جوية للبنتاغون، يظهر فيه المخمس، حيث نسبة طول الوتر إلى طول الضلع يساوي النسبة الذهبية

الرقم الذهبي معروف على الأرجح منذ عصور ما قبل التاريخ. فقد أستعمله مهندسون وفنانون كثيرون منذ العصور القديمة. فمثلا هرم "خوفو"، المبني في سنة 2800 ق.م. تقريبا، يظهر أن مهندسه استعمل الرقم الذهبي وكذلك شأن مبنى "البارثينون" بأثينا، الذي تم بناؤه في القرن الخامس ق.م وأيضا يوجد إشارة إلى هذه النسبة في بناء أهرامات الجيزة في مصر.

وفي عصر النهضة، استعمل العديد من الرسّامين (مثل "بييرو ديلاّ فرانشيسكا" أو "ليوناردو دا فينشي") المظاهر الجمالية المرتبطة بالرقم الذهبي في لوحاتهم. وقد أبرز "دا فينشي" كذلك كتابا يبيّن الخصائص الرياضية والجمالية والعجيبة للرقم الذهبي ويسمى هذا الكتاب " "De divina proportio (أو التناسب الإلهي) وقد ألفه كاهن إيطالي اسمه "فرا لوكا باشيولي".

و يظهر الرقم الذهبي كذلك في ميدان الموسيقى ذلك أن صانع الكمانات الإيطالي "أنتونيو ستراديفاري" (و اشتهر "ستراديفاريوس") استخدم هو الآخر هذا الرقم في صنع كماناته الشهيرة مع نهاية القرن السابع عشر للميلاد.

و في القرن العشرين، أهتم العديد من المهندسين والرسامين بالرقم الذهبي في إنجازاتهم، وبالخصوص المهندس الفرنسي "لو كوربيسيي" والرسّام الإسباني "سلفادور دالي".

ورغم الأقوال بوجود استخدام للنسبة الذهبية في بعض المباني غير أن كثيراً منها هي أما مقاربات بعيدة عن النسبة الذهبية، أو أنها غير موجودة ببساطة كما في المعبد اليوناني الذي ثبت عدم وجود النسبة الذهبية فيه، فضلاً عن وجود نسب أخرى تُستخدم بكثرة من قبل المعماريين لكنها غير مشهورة.

ويدعي البعض انه يستخدم أيضًا في الأسواق المالية وأسواق العملات والمعادن، بل هو من أهم الأدوات المستخدمة في التحليل الفني لتلك الأسواق؛ فعندما تقوم أسعار الأوراق المالية - أو العملات أو المعادن - بتصحيح مسارها (بمعنى أن تنخفض بعد اتجاه صعودي، أو ترتفع بعد اتجاه هبوطي) يقوم المحللون الفنيون لتلك الأسواق بحساب نسب ارتدادات الأسعار (أي تحديد مدى ذلك الارتفاع أو الانخفاض)، وتلك النسب كلها مشتقة من الرقم الذهبي بحسب الادعاءات ولكن لا توجد اي أدلة على ادعاءات مماثلة.

خصائصه

بالإضافة إلى ميزاته الجمالية، فإن الرقم الذهبي يمتاز بخاصية جبريّة مهمّة، إذ أنه يكفي أن تضيف إليه 1 لتجد مربّعه (أي $\varphi \times \varphi$). وبعبارة أخرى فإن :

$\varphi ^{2}=\varphi +1$

و هذه الصيغة الأخيرة هي الصيغة العامة لتعريف الرقم الذهبي.

و هناك خاصية أخرى تنجرّ عن السابقة وهي أنه يكفي أن ننقص الرقم الذهبي من 1 حتى نجد مقلوبه (أي $1 \over \varphi$) وبالتالي فإن :

1 -${1 \over \varphi }=\varphi$

بصورة عامة، يمكن القول أنَّ : $\varphi ^{n}=\varphi ^{n-1}+\varphi ^{n-2}$

وأيضاً: ${\frac {n}{\varphi }}=n\varphi -n$

طريقة استنتاج كل من العلاقات السابقة

• أولاً: لإثبات أن $\varphi ^{2}=\varphi +1$

$\varphi ={\frac {\varphi }{1}}={\frac {\varphi +1}{\varphi }}\;$

بما أن جداء طرفي كسرين متكافئين يساوي جداء وسطيه، فإن:

$\varphi ^{2}=\varphi +1\!$

• ثانياً: إثبات أن ${\frac {1}{\varphi }}=\varphi -1$ نثبت أن جداء الطرفين يساوي جداء الوسطين، فنثبت أن:

$1\times 1=\varphi \times (\varphi -1)\!$

باختزال العلاقة السابقة:

$1=\varphi ^{2}-\varphi \!$

نعوض $\varphi ^{2}=\varphi +1$ فنحصل على:

$1=\varphi +1-\varphi =1\!$

فينتج من تساوي العلاقة السابقة أن جداء طرفي الكسر يساوي جداء وسطيه، وبالتالي تثبت صحة العلاقة: ${\frac {1}{\varphi }}=\varphi -1$

• ثالثا: إثبات أن $\varphi ^{n}=\varphi ^{n-1}+\varphi ^{n-2}$ :

نكتب :

$\varphi ={\frac {\varphi ^{n-1}}{\varphi ^{n-2}}}\!$

العلاقة السابقة صحيحة لأنه عند قسمة عددين ذوي أساسين متساويين فإن الناتج يكون نفس الأساس مرفوع إلى حاصل طرح الأسس

بالاستفادة من علاقة النسبة الذهبية نقول:

${\frac {\varphi ^{n-1}}{\varphi ^{n-2}}}={\frac {\varphi ^{n-1}+\varphi ^{n-2}}{\varphi ^{n-1}}}\!$

$\varphi ={\frac {\varphi ^{n-1}+\varphi ^{n-2}}{\varphi ^{n-1}}}={\frac {\varphi ^{n}}{\varphi ^{n-1}}}\!$

نضرب طرفي المعادلة بـ $\varphi ^{n-1}$ فنحصل على القانون: $\varphi ^{n}=\varphi ^{n-1}+\varphi ^{n-2}$

• رابعاً: إثبات أن ${\frac {n}{\varphi }}=n\varphi -n$

يمكن القول أن:

${\frac {n}{\varphi }}=n\times ({\frac {1}{\varphi }})$

نعوض ${\frac {1}{\varphi }}=\varphi -1$ فنقول:

${\frac {n}{\varphi }}=n\times (\varphi -1)\!$

باختزال ما سبق نحصل على القانون:

${\frac {n}{\varphi }}=n\varphi -n\!$

تجلياته

يظهر الرقم الذهبي في العديد من الإنجازات الإنسانية، ولكن أيضا في الطبيعة بعض الأحيان وبشكل تقريبي مثل:

نجمة خماسية منتظمة، تكون نسبة طول ضلع النجمة إلى طول ضلع المخمس يساوي النسبة الذهبية.

• الشكل الهندسي لنجم البحر الذي يمتاز بشكل خماسي الأضلاع المتداخل.
• شكل قوقعة الحلزون الهندسي، وقد تم تفنيد هذا الظهور للنسبة الذهبية حيث الحلزون الذهبي هو واحد من الأرقام اللانهائية لأي خوارزمية حلزونية ممكنة ولا يشترط أن تكون النسبة الذهبية داخلة.
• أو في زهرة دوار الشمس أو في حراشف الصنوبر ("تفاح الصنوبر").
• ويبدو أيضا أن خارج قسمة الطول الإجمالي لجسم الإنسان على ارتفاع السرة عن الأرض مساو، هو الآخر، للرقم الذهبي.

موقع الكعبة المشرفة

موقع الكعبة في مكة بالنسبة للمسافة بين القطب الشمالي والجنوبي تم حسابهُ من قبل البعض والقول بأنه يساوي 1.618 وأن ذلك دليل على اعجاز الهي حيث لا يستطيع البناء الذي بناها النبي إبراهيم مهما أوتي من علم ان يحددها بهذه الدقة كما أشار القائلين بذلك لإمكانية الرجوع لخرائط جوجل في موقع جوجل إيرث.

لنقم بإجراء الحسابات في البداية ثم نعلق لاحقاً: عند حساب المسافة بين الكعبة والقطب الشمالي تعادل: 7,700.97 ميلاً، في حين أن المسافة بين الكعبة والقطب الجنوبي تعادل: 4,739.73 ميلاً، فتكون المسافة الكلية بين القطبين الشمالي والجنوبي بذلك: 12,440.70 ميلاً.

لا شك أنها مسافات تقريبية محددة بدقة منزلتين بعد الفاصلة العشرية (جزء من المئة من الميل).

إذا قمنا بحساب نسبة أكبر المسافتين إلى أصغرهما، فسنجد أن الناتج هو 1.6247 كما أن تقسيم مجموعهما على العدد الأكبر منهما يساوي 1.6155وهو قريب جداً من النسبة الذهبية.

وهنا لدينا تعليقان: أولاً، قد يعزى الاختلاف البسيط بين الناتج المحسوب والقيمة الحقيقية للنسبة الذهبية إلى الدقة المحدودة في حساب المسافة كما أشرنا سابقاً. ثانياً، رغم استبعاد الصدفة في هذا الحساب، إلا أننا لا نجزم غيباً أن الله سبحانه وتعالى أراد من هذا الحساب الإعجاز أو الربط مع النسبة الذهبية التي قدرها هو سبحانه، فالله أعلم بمراده وحكمته، وكل ما نستطيع فعله هو الحساب والتأمل، وذلك لكي لا نقول على الله ما لم يقله.

حذف لعدم صحة الأرقام:

، غير أن هذا الادعاء صحيح ومؤكد حيث ان: المسافة بين القطبين (مرورا بالكعبة المشرفة) = 18,883.48 كم المسافة بين القطب الجنوبي والكعبة = 11,823 كم المسافة بين الكعبة والقطب الشمالي =7,073 كم وخلال قسمه 11823/7073 نحصل على تقريب النسبة الذهبية ~1.618, يوجد انواع اخرى لاثبات النسبة الذهبية للكعبة عن طريق العرض والقطر.

انظر أيضًا

• متتالية فيبوناتشي
• الزاوية الذهبية
• فيبوناتشي
• متوسط ذهبي
• الرياضيات في الطبيعة

وصلات خارجية

• إيريك ويستاين، نسبة ذهبية، ماثوورلد Mathworld (باللغة الإنكليزية).