نظرية البيان
| صنف فرعي من | |
|---|---|
| جزء من | |
| يمتهنه | |
| فروع | |
| الموضوع |

نظرية المخططات أو نظرية البيان (بالإنجليزية: Graph theory) هي نظرية في الرياضيات وعلوم الحاسب، تدرس خواص المخططات حيث يتم تمثيل مجموعة كائنات تدعى رؤوساً، ترتبط ببعضها بأضلاع وتدعى أحيانا أقواساً، يمكن أن تكون موجهة أي مزودة باتجاه (تستخدم الاسهم بدل الأضلاع) أو بدون اتجاه (أضلاع فقط). التمثيل لهذا المخطط يكون على الورق بمجموعة نقاط تمثل الرؤوس متصلة بخطوط هي حروف (أضلاع أو أسهم) المخطط. رياضياً يُمكن أن يُعطى المخطط عبر مصفوفة المجاورة (Adjacency Matrix).
تُمكن الاستعانة بالمخططات من حلحلة الكثير من المشاكل العملية، فمثلا بنية موسوعة ويكيبيديا يمكن تمثيلها بمخطط رؤوسه هي أسماء المقالات ونقوم برسم خط موجه بين مقالتين من أ إلى ب إذا كانت المقالة أ تحوي رابطا إلى المقالة ب. تطبيقات هذه النظرية واسعة جدا ولحل مشاكلها يستخدم الحاسوب بشكل واسع. لذلك تهتم علوم الحاسوب بتصميم خوارزميات لنظرية المخططات حيث يمكن معالجة أي مخطط لتمييز خصائصه واستخلاص المعلومات منه.
التاريخ[عدل]

يعد البحث الذي كتبه ليونهارد أويلر ونشره في عام 1736 حول موضوع جسور كونيغسبرغ السبعة أول بحث في التاريخ في نظرية المخططات.[2] هذا البحث بالإضافة إلى المقالة التي كتبها فانديرموند عن مسألة الفارس، بالإضافة إلى العمل الذي قام به غوتفريد لايبنتز في وضع علاقات لعدد الرؤوس بالأضلاع وأوجه متعددات السطوح المحدبة تعتبر بدايات لعلم الطوبولوجيا.
تعاريف[عدل]
البيان (Graph)[عدل]
هو زوج مرتب يشمل مجموعة من الرؤوس ومجموعة من الأضلاع والتي هي بدورها مجموعة ثنائيات جزئية غير مرتبة من ويعرف هذا النوع من البيانات بالبيان البسيط غير الموجه.
- إذا كان الضلع مزوداً باتجاه (سهم) أصبح البيان موجهاً وأصبحت مجموعة الأضلاع مجموعة ثنائيات مرتبة من .
-
بيان موجه
-
بيان غير موجه
ترتيب البيان [عدل]
هو عدد عقد (رؤوس) البيان (مثال: بيان فيه 3 رؤوس هو بيان من المرتبة الثالثة).
حجم البيان [عدل]
هو عدد حروف (أضلاع) البيان.
درجة العقدة[عدل]
- درجة عقدة (رأس) البيان الغير موجه: : هي عدد الأضلاع المتصلة بالعقدة.
- درجة عقدة (رأس) البيان الموجه : يوجد نوعان من الدرجات
- درجة الدخول للعقدة : وهي عدد الأضلاع الداخلة إلى عقدة.
- درجة الخروج للعقدة : وهي عدد الأضلاع الخارجة من عقدة.
درجة البيان[عدل]
- درجة البيان غير الموجه : هي مجموع درجات العقد فيه.
حيث:
- درجة البيان الموجه :
- درجة الدخول : هي مجموع درجات دخول العقد.
- درجة الخروج : هي مجموع درجات خروج العقد.
حيث:
مثال:
بيان غير موجه تحمل كل عقدة فيه درجتها وتكون درجته:
أنواع البيانات[عدل]
1- البيان البسيط (Simple Graph)[عدل]
هو بيان لا يحوي حلقة ذاتية (Self-loop) أو أضلاع مكررة (Multiple-edges).
-
بيان بسيط
2- البيان المتعدد (Multigraph)[عدل]
هو بيان لا يحوي حلقة ذاتية (Self-loop) ولكن يحتوي على الأقل على ضلع مكرر (Multiple-edge).
-
بيان متعدد
3- البيان الزائف أو شبه البيان (Pseudograph)[عدل]
هو بيان يحوي حلقات ذاتية (Self-loops) وأضلاع مكررة (Multiple-edges).
-
بيان زائف
4- البيان المنتظم (Regular Graph)[عدل]
نقول عن بيان أنه منتظم من الدرجة إذا كانت درجة كل عقدة من البيان هي .
-
بيان منتظم من الدرجة 3
5-الطريق (Walk)[عدل]
الطريق في بيان هو متتالية متناوبة من العقد والأضلاع: تبدأ وتنتهي بالعقد بحيث أن .
- (e دلالة على الضلع و v دلالة على العقدة)
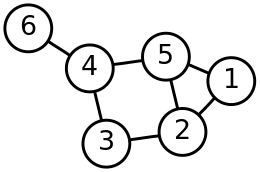
في الشكل 1 :
هو طريق طوله 4 (طول الطريق يعرف بعدد أضلاعه).
6-القافلة (Trail) والمسار (Path)[عدل]
- القافلة: هي طريق لا يحوي أضلاع مكررة.
من الشكل 1 نجد القافلة التالية:
- المسار: هو طريق لا يحوي عقد مكررة.
-
مسار يحوي 6 عقد
- كل مسار هو قافلة ولكن العكس غير صحيح.
7- الحلقة (Cycle Graph)[عدل]
هي مسار يبدأ وينتهي بنفس العقدة. في الشكل 1 نجد الحلقة التالية:
- .
8- البيان التام أو الكامل (Complete Graph)[عدل]
هو بيان من المرتبة فيه كل عقدتين متمايزتين متصلتين ونرمز له بـ .
البيان التام من المرتبة هو بيان منتظم من المرتبة وحجمه يعطى بالعلاقة:
-
بيان كامل
9- العجلة (Wheel Graph)[عدل]
إذا كانت لدينا حلقة Cn. فالعجلة فيها رأس واحد يجاور جميع رؤوس البيان الأخرى ورمز العجلة Wn
بعض البيانات الخاصة[عدل]
1- بيان هيوود (Heawood Graph)[عدل]
هو بيان فيه 14 عقدة و21 ضلع.
2- بيان نيسر (Kneser Graph)[عدل]
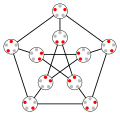
3- بيان بيترسن (Petersen Graph)[عدل]
-
الشكل الأكثر شهرة لبيان بيترسن
تعاريف إضافية[عدل]
الارتباط والجوار[عدل]
إذا كانت قمتين من مخطط مرتبطتان بحرف، نقول أنهما متجاورتان أو مرتبطتان.
مربع مخطط[عدل]
مربع مخطط هو مخطط له نفس قمم المخطط الأول وله نفس الحروف أو الأقواس بالإضافة إلى وجود حروف أو أقواس تربط بين القمم التي لها جوارات مشتركة.
سلاسل وسبل[عدل]
السلسلة أو السبيل هو جزء من مخطط يربط بين قمتين بواسطة أزواج قمم مرتبط مثنى مثنى على التوالي.
البئر[عدل]
البئر هو عقدة في بيان موجه درجة خروجه منعدمة. أي:
المنبع[عدل]
المنبع هو عقدة في بيان موجه درجة دخوله منعدمة. أي:
مخطط مكمل[عدل]
المخطط المكمل لمخطط هو مخطط له نفس القمم مرتبطة إذا لم تكن مرتبطة في المخطط الأصلي.
مسار ومسار مغلق[عدل]
المسار هو سلسلة رؤوس مرتبطة، لها بداية ونهاية (نقطة انطلاق ونقطة وصول).
إذا كانت نقطتي الانطلاق والوصول منطبقتين، المسار يكون مغلقا.
مسار أولير[عدل]
مسار أولير لمخطط G غير موجه هو مسار يمر بكل الحروف مرة واحدة فقط.
نقول أن المخطط متصل إذا كان يحتوي على مسار أولير، وكل رؤوسه من درجة مزدوجة
مسار هاميلتون[عدل]
مسار هاميلتون لمخطط G هو مسار يمر بكل القمم مرة واحدة فقط.
مخطط كامل[عدل]
المخطط الكامل هو مخطط بسيط يكون كل زوج من رؤوسه متصلان بضلع. بحيث أن المخطط الكامل ذو n رأس يكون له n(n-1)/2 ضلع.
مخطط مستقر[عدل]
المخطط المستقر هو مخطط ليس له حروف.
مخطّط مستوي[عدل]
المخطط المستوي هو مخطط يمكن تمثيله بكيفية لا تتقاطع الحروف فيه.
مخطط قوي التوصيل[عدل]
مخطط يمكن الوصول فيه من أي عقدة إلى أي عقدة أخرى.
تمثيلات[عدل]
كل مخطط يضم مجموعة قمم يمكن تمثيلها على شكل دوائر، إذا كان المخطط موجه يتم تمتيل كل قوس بسهم، وبخط في حالة مخطط عادي.
مسائل[عدل]
انظر أيضاً[عدل]
| في كومنز صور وملفات عن: نظرية البيان |
مراجع[عدل]
- ^ الاقتباس: Discrete Mathematics > Graph Theory. الوصول: 19 يناير 2018. وصلة مرجع: http://mathworld.wolfram.com/topics/GraphTheory.html.
- ^ Biggs, N.; Lloyd, E. and Wilson, R. (1986). Graph Theory, 1736-1936. Oxford University Press.
{{استشهاد بكتاب}}: صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link)