أسطوانة (هندسة)
في الرياضيات، الأسطوانة من المجسمات الأساسية، وهي أي مجسم يتشكل سطحه من جميع النقاط التي تبعد مسافة معينة عن قطعة مستقيمة معطاة تسمى محور الأسطوانة ويسمى الحيز المغلق بمستويين متوازيين يتعامدان مع محور الأسطوانة، ويمكن تعريفه كأي مجسم ينتج من دوران مستطيل حول أحد أضلاعه دورة كاملة، ويسمى محور الدوران بـ محور الأسطوانة والضلع المقابل لهُ يسمى بـالمولد أو الراسم للأسطوانة.[1][2][3] كما أن موشور قاعدته يشكل دائرة، والدائرتين التي تحد المجسم من الجهتين تسمى قاعدة أو دليل، والقطعة المستقيمة التي تتعامد مع القاعدتين تسمى ارتفاع الأسطوانة، إذا كان ارتفاع الأسطوانة يتعامد مع محيط قاعدتي الأسطوانة سميت أسطوانة قائمة وإلا سميت أسطوانة مائلة.[4])
إذا قيل أسطوانة بدون تحديد فإننا نقصد الأسطوانة الدائرة القائمة.
الأسطوانة التي مقطعها العرضي هو قطع زائد أو قطع ناقص أو قطع مكافئ تسمى الأسطوانة الزائدة والأسطوانة الناقصة والأسطوانة المكافئة على التوالي، ولا تنطبق عليها التعريفات السابقة.
قوانين عامة[عدل]
- هذه القوانين حول الأسطوانة الدائرة القائمة
- r: نصف قطر القاعدة.
- h: ارتفاع الأسطوانة أو محورها.
- A: مساحة القاعدة ويمكن حسابة عن طريق
- P: محيط القاعدة، ويمكن حسابة عن طريق
مساحات[عدل]
- المساحة الجانبيه = محيط القاعدة × الارتفاع =
- مساحة القاعدة العليا =
- مساحة القاعدة السفلى =
- المساحة الكلية = .[5]
الحجم[عدل]
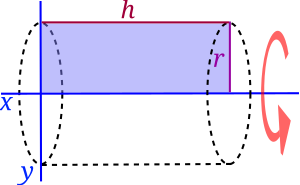
- يمكن ايجاد حجم الأسطوانة مثل ايجاده في المنشور:
- بضرب مساحة القاعدة في الارتفاع =
- d: هو القطر (ق)
- ويمكن التوصل لنفس النتيجة باعتبار الأسطوانة مجسم دوراني ينشأ عن دوران دالة ثابتة حول المحور السيني
- إذن يمكن حساب الحجم عن طريق =
سبب التسمية[عدل]
لقد سميت الأسطوانة باسمها: أسطوانة الدوران، لأن بها مولدا أو ما يسمى (مولد الدوران)
انظر أيضا[عدل]
مصادر[عدل]
- ^ Albert 2016، p. 43
- ^ "MathWorld: Cylindric section". مؤرشف من الأصل في 2018-01-15.
- ^ Slaught، H.E.؛ Lennes، N.J. (1919)، Solid Geometry with Problems and Applications (PDF) (ط. Revised)، Allyn and Bacon، ص. 79–81، مؤرشف من الأصل (PDF) في 2019-09-27
- ^ κύλινδρος, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus نسخة محفوظة 15 مارس 2016 على موقع واي باك مشين.
- ^ Lax، Peter D.؛ Terrell، Maria Shea (2013)، Calculus With Applications، كتب جامعية في الرياضيات، Springer، ص. 178، ISBN:9781461479468، مؤرشف من الأصل في 2020-02-13.
| أسطوانة في المشاريع الشقيقة: | |
| |
| جزء من سلسلة مقالات حول |
| الهندسة الرياضية |
|---|
 |
| علماء الهندسة |
| بوابة هندسة رياضية |









![{\displaystyle \pi \times \int _{0}^{h}[d(x)]^{2}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/707961a91126d155295b50398a5e138576179947)