قاعدة شبه المنحرف


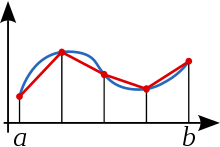
في الرياضيات، قاعدة شبة المنحرف (بالإنكليزية: Trapezoidal rule) هي إحدى طرق الحساب التقريبي للتكامل المحدد.
تعمل قاعدة شبه المنحرف بتقريب المنطقة تحت منحنى الدالة بشبه منحرف وحساب مساحته. ينجم عن ذلك
لحساب التكامل بدقة أفضل، يمكن فصل فترة التكامل أولا إلىn فترات أصغر، ومن ثم تطبيق قاعدة شبه المنحرف على كل فترة. يمكن تحصيل قاعدة شبه المنحرف المركب:
ويمكن صياغة هذا بشكل اخر:
حيث
تحليل الخطأ[عدل]
يعرف الخطأ في قاعدة شبه المنحرف بأنه الفرق بين قيمة التكامل والقيمة العددية:
يمكن كتابة هذا الخطأ بالشكل
حيثξ عدد ما بين a وb.[1]
يعطى تخمين الخطأ المقارب لـ n → ∞ بالعلاقة
الحدود الأخرى لهذا الخطأ يمكن إيجادها من صيغة مجموع أويلر-ماكلورين.
البرمجة[عدل]
مثال على قاعدة شبه المنحرف مكتوب بلغة البايثون
#!/usr/bin/env python
def trapezoidal_rule(f, a, b, N):
"""Approximate the definite integral of f from a to b by the
composite trapezoidal rule, using N subintervals"""
return (b-a) * (f(a)/2 + f(b)/2 + sum([f(a + (b-a)*k/N) for k in range(1,N)])) / N
#test
print trapezoidal_rule(lambda x:x**9, 0.0, 10.0, 100000)
إنظر أيضا[عدل]
ملاحظات[عدل]
- ^ Atkinson (1989), equation (5.1.7)
- ^ Atkinson (1989), equation (5.1.9)
مراجع[عدل]
- Atkinson، Kendall A. (1989)، An Introduction to Numerical Analysis (ط. 2nd)، New York: جون وايلي وأولاده ، ISBN:978-0-471-50023-0
{{استشهاد}}: صيانة الاستشهاد: علامات ترقيم زائدة (link). - Burden، Richard L. (2000)، Numerical Analysis (ط. 7th Ed.)، Brooks/Cole، ISBN:0-534-38216-9
{{استشهاد}}:|طبعة=يحتوي على نص زائد (مساعدة) والوسيط author-name-list parameters تكرر أكثر من مرة (مساعدة).
| في كومنز صور وملفات عن: قاعدة شبه المنحرف |




![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{n}}\left[{f(a)+f(b) \over 2}+\sum _{k=1}^{n-1}f\left(a+k{\frac {b-a}{n}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/426f913409debfd041d6dc36be8820f8c57dabe8)


![{\displaystyle {\text{error}}=\int _{a}^{b}f(x)\,dx-{\frac {b-a}{n}}\left[{f(a)+f(b) \over 2}+\sum _{k=1}^{n-1}f\left(a+k{\frac {b-a}{n}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0f0d5f32b3080c6b232bf51e2eaf050e78f3132)

