فضاء هيلبرت
| صنف فرعي من | |
|---|---|
| سُمِّي باسم | |
| يُصوِّر |
المفهوم الرياضياتي لفضاء هيلبرت (بالإنجليزية: Hilbert space) يعمم مفهوم الفضاء الإقليدي.[1][2][3] فهو فضاء معياري معرف عليه دالة الجداء الداخلي بشرط أن يكون المعيار المعرف عليه هو بدلالة دالة الجداء الداخلي هذه، بالإضافة إلى وجوب كونه فضاء معياريا كاملا أو ما يدعى ب فضاء باناخ. وهذا يعني أن أي فضاء هيلبرت هو فضاء باناخ ولكن العكس غير صحيح. مثال على ذلك، الفضاء Q هو فضاء منتظم تحت النظيم العادي ولكنه ليس بفضاء بانخ.
يمكننا فضاء هلبرت من تعميم أساليب الجبر الخطي والتفاضل والتكامل المستخدمة في الفضاءات الإقليدية ثنائية الأبعاد وثلاثية الأبعاد إلى فضاءات قد تكون لانهائية البُعد. فضاء هلبرت هو فضاء متجهي مزود بجداء داخلي، وبذا يسمح بتعريف دالة مسافة وتعامد. وإضافة لذلك، فإن فضاء هلبرت هو فضاء متري كامل مع دالة المسافة المعرفة فيه (في هذه الحالة هي دالة المعيار)، مما يعني توفر النهايات التي تسمح باستخدام التفاضل والتكامل.
فضاءات هلبرت تظهر بشكل طبيعي كثيرًا في الرياضيات والفيزياء، عادةً كفضاء دالي لا نهائي الأبعاد. أقدم فضاءات هلبرت دراسةً كانت على يد ديفيد هيلبرت وإرهارد شميدت وفريجيس ريش "Frigyes Riesz" في العقد الأول من القرن العشرين. وتعتبر من الأدوات الهامة في المعادلات التفاضلية الجزئية، وميكانيكا الكم، وتحليل فورييه (الذي يتضمن تطبيقات لمعالجة الإشارات ونقل الحرارة)، ونظرية إرجوديك (التي تشكل الأساس الرياضي للديناميكا الحرارية). صاغ جون فون نيومان مصطلح فضاء هيلبرت للمفهوم التجريدي المستخدم في العديد من هذه التطبيقات المتنوعة. أدى نجاح أساليب فضاء هيلبرت إلى ازدهار التحليل الدالي. بعيدًا عن الفضاءات الإقليدية الكلاسيكية، فإن من أمثلة فضاءات هيلبرت فضاءات الدوال الكمولة تربيعيًا "Lp space"، وفضاءات المتسلسلات "Sequence space"، وفضاءات سوبوليف "Sobolev space" المكونة من دوال معممة، وفضاءات هاردي "Hardy space" للدوال تامة الشكل.
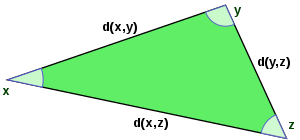
يلعب الحدس الهندسي دورًا مهمًا في العديد من جوانب نظرية فضاء هلبرت. توجد نظائر مطابقة لنظرية فيثاغورس وقانون متوازي الأضلاع في فضاء هلبرت. على مستوى أعمق، يلعب الإسقاط العمودي على فضاء جزئي (مناظر لـ «إسقاط ارتفاع» المثلث) دورًا مهمًا في مسائل التحسين وجوانب أخرى في النظرية. يمكن تحديد بشكل فريد عنصر في فضاء هيلبرت عن طريق إحداثياته المنسوبة لزمرة من محاور الإحداثيات (متعامدة القاعدة في فضاء هلبرت)، على غرار الإحداثيات الديكارتية في المستوى. عندما تكون هذه المجموعة من المحاور معدودة غير منتهية، في هذه الحالة يمكن النظر لفضاء هيلبرت على أنه فضاء متسلسلات لانهائية التي يمكن جمعها تربيعيًا. فضاء المتسلسلات اللانهائية هذا هو ما يشار إليه في كثير من الأحيان في الأدبيات الرياضية القديمة بفضاء هلبرت. المؤثرات الخطية في فضاء هلبرت أيضًا لها حضور كبير: في الحالات الجيدة، هي تحويلات تساهم في تمديد الفضاء بواسطة عوامل مختلفة في اتجاهات متعامدة تبادليًا بصورة دقيقة تظهر من خلال دراسة طيفها.
تعريف وتوضيح[عدل]
مثال تحفيزي: فضاء المتجه الإقليدي[عدل]
أحد الأمثلة الأكثر شيوعًا لفضاء هيلبرت هو فضاء المتجه الإقليدي المكون من متجهات ثلاثية الأبعاد، وعملية الجداء النقطي، ويُشار إليه بالرمز R3. عملية الجداء القياسي تأخذ متجهين x وy وينتج عنها عدد حقيقي x ⋅ y. لو مثلنا x وy بالإحداثيات الديكارتية، فإن حاصل الجداء القياسي يكون:
الجداء النقطي يستوفي الخصائص التالية:
- متماثل في x و y: x ⋅ y = y ⋅ x
- خطي لأول جزء من العنصر: (ax1 + bx2) ⋅ y = ax1 ⋅ y + bx2 ⋅ y لأي قيمة عددية a و b والمتجهات x1 وx2 وy
- محدد إيجابيا: لجميع المتجهات x، x ⋅ x ≥ 0 ، ويساوي الصفر إذا وفقط إذا كان x = 0
الجداء النقطي الذي يتم إجراؤه على أزواج المتجهات والمستوفي لهذه الخصائص الثلاث، يعرف بالجداء الداخلي (الحقيقي). فضاء المتجه الحاوي لهذا الجداء الداخلي الحقيقي يُعرف كـ فضاء جداء داخلي (حقيقي). كل فضاء جداء داخلي ذو أبعاد محدودة هو أيضًا فضاء هيلبرت.[4] الخاصية الأساسية للجداء النقطي التي تربطه بالهندسة الإقليدية هي أنه مرتبط بطول (أو معيار) المتجه، المشار إليه بـ ||x|| ، والزاوية θ بين متجهين x و y عن طريق الصيغة:
حساب التفاضل والتكامل متعدد المتغيرات في الفضاء الإقليدي يعتمد على حساب النهايات، وللحصول على معايير مفيدة لاستنتاج وجود النهايات. فإن المتسلسلة الرياضية
غالبًا ما يغلب استخدام الأعداد المركبة في فضاءات هلبرت. فالمستوى العقدي المشار له بـ C يحوي مفهوم الحجم، والقيمة المطلقة |z| المُعَّرَف بأنه الجذر التربيعي لجداء z مع مرافقه المركب:
المثال الثاني هو الفضاء C2 الذي تتكون عناصره من أزواج من الأعداد المركبة z = (z1, z2). وحاصل الجداء الداخلي لـ z مع متجه آخر w = (w1, w2)يعطى بالصيغة التالية:
تعريف[عدل]
فضاء هلبرت H هو فضاء جداء داخلي حقيقي أو مركب وهو أيضًا فضاء متري كامل مع دالة المسافة الناتجة عن الجداء الداخلي.[6]
عندما نقول أن H هو فضاء جداء داخلي مركب فإننا نعني أن H هو فضاء متجهي مركب يحوي جداء داخلي يربط كل زوج من العناصر في H بعدد مركب، ويتمتع هذا الجداء بالخصائص التالية:
- الجداء الداخلي مترافق متناظر؛ أي أن الجداء الداخلي لزوج من العناصر يكافئ المرافق المركب للجداء الداخلي لنفس العناصر مع تبديل ترتيبها:
- الجداء الداخلي خطي لأول جزء من العنصر [7] لجميع الأعداد المركبة و
- الجداء الداخلي لعنصر مع نفسه هو إيجابي منتهي:
نستنتج من الخاصيتين 1 و 2 أن الجداء الداخلي المركب هو اقتران غير خطي "antilinear map"، ويسمى أيضًا "conjugate linear"، للجزء الثاني من العنصر، بمعنى أن:
المعيار هي دالة حقيقية القيمة تعرف على النحو التالي:
والمسافة بين نقطتين في H تُعَرَّف عن طريق المعيار بالشكل التالي:
هذه الخاصية الأخيرة هي في الأخير نتاج لمتباينة كوشي -شوارتز، والتي تؤكد أن:
بوجود دالة مسافة مُعَرَّفة بهذا الشكل، فإن أي فضاء جداء داخلي هو فضاء متري، ويُعرف أحيانًا باسم «فضاء هاوسدورف ما قبل هلبرت» (Hausdorff pre-Hilbert space).[9] أي فضاء ما قبل هلبرت وأيضًا فضاء كامل فهو فضاء هيلبرت.
يُعبر عن اكتمال H باستخدام نموذج من اختبار كوشي للمتسلسلات في H: ففضاء ما قبل هلبرت H مكتمل إذا كان كل متسلسلة كوشية تتقارب بالنسبة للمعيار إلى عنصر في الفضاء. يمكن وصف الاكتمال بالشرط المكافئ التالي: إذا كانت متسلسلة المتجهات
ولأن فضاءات هلبرت معيارية كاملة، فإنها بالتعريف هي أيضًا فضاءات باناخ. ولذا فهي فضاءات متجهات طوبولوجية، حيث مفاهيم الطوبولوجيا مُعَرَفَة بشكل جيد مثل انفتاح وانغلاق المجموعات الفرعية. لفكرة الفضاء الجزئي الخطي المغلق في فضاء هلبرت أهمية خاصة، حيث يصبح فضاءًا مكتملًا أيضًا مع الجداء الداخلي المُقَيد، (كونه مجموعة مغلقة في فضاء متريّ كامل) وبالتالي فهو فضاء هيلبرت في حد ذاته.
المثال الثاني: فضاءات المتسلسلات[عدل]
فضاء المتسلسلة الذي يرمز له بـ l2 يتكون من جميع المتتاليات اللانهائية z = (z1, z2, …) من الأعداد المركبة بحيث تكون المتسلسلة
شرط اكتمال الفضاء متحقق طالما أن متسلسلة من العناصر من l2 تتقارب مطلقًا بالنسبة للمعيار، إذا فإنها تتقارب لـ عنصر في l2. يعتبر البرهان أساسيًا في التحليل الرياضي، ويسمح بالتعامل مع متسلسلة من عناصر الفضاء بنفس السهولة كما في حالة متسلسلة أرقام مركبة (أو متجهات في فضاء إقليدي محدود الأبعاد).[9]
تاريخ[عدل]

قبل فضاءات هلبرت، كانت التعميمات الأخرى للفضاءات الإقليدية معروفة لعلماء الرياضيات والفيزياء. على وجه الخصوص، اكتسبت فكرة الفضاء الخطي المجرد (فضاء المتجهات) بعض الزخم قرب نهاية القرن التاسع عشر:[10] ففي فضاء المتجهات يمكن للمرء جمع المتجهات معا أو ضربها في كميات قياسية (مثل الأعداد الحقيقية أو المركبة) ولا يشترط بالضرورة أن تكون معبرة عن عناصر هندسية فيزيائية، مثل متجهات الموقع والزخم. في مطلع القرن العشرين درس علماء الرياضيات أيضًا فضاءات يمكن اعتبارها خطية كـ المتواليات (بما في ذلك المتسلسلات) والدوال.[11] فعلى سبيل المثال، في فضاءات الدوال يمكن إضافة الدوال معًا أو ضربها بعدد قياسي ثابت، وهذه العمليات تخضع لنفس القواعد الجبرية التي تنطبق على عمليات الجمع والضرب القياسي في فضاء المتجهات.
في العقد الأول من القرن العشرين، أدت تطورات موازية لظهور فضاءات هلبرت. كان أولها أثناء دراسة ديفيد هيلبرت وإيرهارد شميدت للمعادلات التكاملية،[12] حيث لاحظوا أن الدالتين f و g لهم قيم حقيقية قابلين للتكامل تربيعيا على a, b لهما جداء داخلي بالشكل التالي:
له العديد من الخصائص المعروفة للجداء النقطي الإقليدي. بالتحديد، خاصية فئة الدوال المتعامدة. استغل شميدت تشابه هذا الجداء الداخلي مع الجداء النقطي المعروف لإثبات وجود تناظر بين التفريق الطيفي والمؤثر من الشكل التالي
حيث K دالة متصلة متناظرة في x و y. ويعبر التوسع الذاتي عن الدالة K في صورة متسلسلة من الشكل التالي:
حيث الدوال φn متعامدة بمعنى أن ⟨φn, φm⟩ = 0لجميع القيم n ≠ m يشار أحيانًا للحدود الفردية في هذه المتسلسلة على أنها حلول جداء أولية "elementary product solutions". ومع ذلك، هناك توسعات للدالة الذاتية تفشل في التقارب نحو دالة كمولة تربيعيا: وهنا نشير لأهمية الاكتمال، الذي يضمن حدوث التقارب.[13]
كان التطور الثاني هو تكامل لوبيغ الذي طوره هنري لوبيغ عام 1904 كبديل لتكامل ريمان.[14] وأصبح من الممكن تكامل فئة أوسع بكثير من الدوال. في عام 1907، أثبت كلا من Frigyes Riesz و Ernst Sigismund Fischer بشكل مستقل أن الفضاء L2 لدوال لوبيغ القابلة للتكامل (الكمولة) هو فضاء متري كامل.[15] بسبب مفهوم الاكتمالوتوظيفه هندسيا، فإن نتائج القرن التاسع عشر لجوزيف فورييه وفريدريك بيسيل ومارك أنطوان بارسيفال "Marc-Antoine Parseval" على المتسلسلات المثلثية تم استخدامها بيسر في هذه الفضاءات العامة، مما أنتج أداة هندسية وتحليلية تعرف الآن عادة باسم نظرية ريش فيشر "Riesz–Fischer theorem".[16]
اُثبتت المزيد من النتائج الأساسية في أوائل القرن العشرين. على سبيل المثال، وُضِعَتْ نظرية تمثيل ريش "Riesz representation theorem" بشكل مستقل من قبل موريس فريشيه وفريغيس ريش "Frigyes Riesz" في عام 1907.[17] كما صاغ جون فون نيومان مصطلح فضاء هيلبرت المجرد في عمله على المؤثرات الهرميتية "Hermitian operators" غير المحدودة.[18] على الرغم من أن علماء رياضيات آخرين مثل هيرمان فايل ونوربرت وينر قد درسوا بالفعل بتعمق فضاءات معينة من فضاءات هلبرت، غالبًا من وجهة نظر فزيائية، فإن فون نيومان قدم أول معالجة كاملة مع مسلماتها.[19] واستخدمها فون نيومان لاحقًا في عمله الأساسي في أسس ميكانيكا الكم،[20] وفي عمله مع يوجين ويغنر. وسرعان ما تبنى آخرون اسم «فضاء هلبرت»، مثل هيرمان فايل في كتابه عن ميكانيكا الكم ونظرية المجموعات.[21]
تأكدت أهمية مفهوم فضاء هلبرت بتوفيره واحدة من أفضل الصيغ الرياضية لميكانيكا الكم.[22] وإختصارًا، فإن حالات نظام ميكانيكي كمي هي متجهات في فضاء هيلبرت معين، والمرصودات "observables" هي مؤثرات هرميتية "Hermitian operators" في هذا الفضاء، والمتناظرات في النظام هي مؤثر واحدي "Unitary operator"، والقياسات هي إسقاط عمودي. قدمت العلاقة بين التناظرات الميكانيكية الكمومية والمؤثرات الواحدية حافزًا لتطوير نظرية التمثيل الوحدوي للمجموعات، التي بدأت في عمل هيرمان فايل عام 1928.[21] من ناحية أخرى، في أوائل الثلاثينيات من القرن العشرين أصبح من الممكن وصف الميكانيكا الكلاسيكية بمصطلحات فضاء هيلبرت (ميكانيكا كوبمان-فون نيومان الكلاسيكية "Koopman–von Neumann classical mechanics") وتحليل خصائص معينة للأنظمة الديناميكية الكلاسيكية باستخدام تقنيات فضاء هلبرت في إطار نظرية إرجوديك.[23]
وفقًا لصياغة فيرنر هايزنبرغ لميكانيكا المصفوفة الكمية فإن جبر المرصودات [الإنجليزية] في ميكانيكا الكم هو بطبيعة الحال جبر المؤثرات المعرفة في فضاء هيلبرت.[24] بدأ فون نيومان دراسة جبر المؤثرات في ثلاثينيات القرن العشرين، كحلقة مؤثرات في فضاء هيلبرت. يُعرف نوع الجبر الذي درسه فون نيومان ومعاصروه الآن باسم جبر فون نيومان "Von Neumann algebra".[25] في الأربعينيات من القرن العشرين، قدم إسرائيل جيلفاند ومارك نيمارك "Mark Naimark" وإيرفينغ سيغال تعريفًا لنوع من جبر المؤثرات يُدعى "C*-algebra" الذي لم يشر إلى فضاء هيلبرت، ولكنه استنبط العديد من المميزات المفيدة في جبر المؤثرات السابق دراستها. النظرية الطيفية للمؤثرات الهرميتية على وجه الخصوص والتي تكمن وراء الكثير من نظرية فضاء هلبرت الحالية عُممت على "C * -algebras".[25] هذه التقنيات هي الآن أساسية في التحليل التوافقي التجريدي ونظرية التمثيل.
انظر أيضًا[عدل]
مراجع[عدل]
- ^ "معلومات عن فضاء هيلبرت على موقع jstor.org". jstor.org. مؤرشف من الأصل في 2019-05-25.
- ^ "معلومات عن فضاء هيلبرت على موقع enciclopedia.cat". enciclopedia.cat. مؤرشف من الأصل في 2019-08-15.
- ^ "معلومات عن فضاء هيلبرت على موقع babelnet.org". babelnet.org. مؤرشف من الأصل في 2019-12-10.
- ^ However, some sources call finite-dimensional spaces with these properties pre-Hilbert spaces, reserving the term "Hilbert space" for infinite-dimensional spaces; see, e.g., Levitan 2001.
- ^ Marsden 1974
- ^ The mathematical material in this section can be found in any good textbook on functional analysis, such as Dieudonné (1960), Hewitt & Stromberg (1965), Reed & Simon (1980) or Rudin (1987).
- ^ In some conventions, inner products are linear in their second arguments instead.
- ^ Schaefer & Wolff 1999.
- ^ أ ب Dieudonné 1960
- ^ Largely from the work of Hermann Grassmann, at the urging of August Ferdinand Möbius (Boyer & Merzbach 1991, pp. 584–586). The first modern axiomatic account of abstract vector spaces ultimately appeared in Giuseppe Peano's 1888 account (Grattan-Guinness 2000; O'Connor & Robertson 1996).
- ^ A detailed account of the history of Hilbert spaces can be found in Bourbaki 1987.
- ^ Schmidt 1908
- ^ Titchmarsh 1946
- ^ Lebesgue 1904. Further details on the history of integration theory can be found in Bourbaki (1987) and Saks (2005).
- ^ Bourbaki 1987.
- ^ Dunford & Schwartz 1958
- ^ In Dunford & Schwartz (1958), the result that every linear functional on L2[0,1] is represented by integration is jointly attributed to Fréchet (1907) and Riesz (1907). The general result, that the dual of a Hilbert space is identified with the Hilbert space itself, can be found in Riesz (1934).
- ^ von Neumann 1929.
- ^ Kline 1972
- ^ Hilbert, Nordheim & von Neumann 1927
- ^ أ ب Weyl 1931.
- ^ Prugovečki 1981.
- ^ von Neumann 1932
- ^ Peres 1993.
- ^ أ ب Murphy 1990
| فضاء هيلبرت في المشاريع الشقيقة: | |
| |