بعد

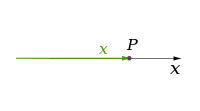
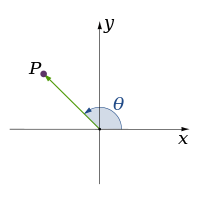
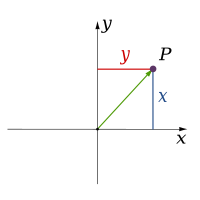
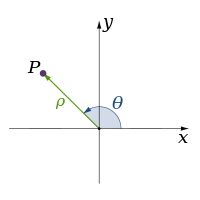
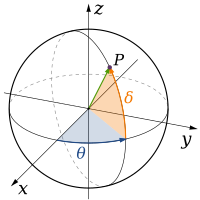
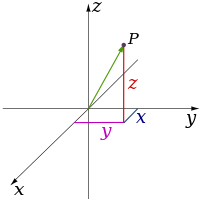
البُعد في الفيزياء والرياضيات يعرف لمكان أو لجسم بالحد الأدنى للإحداثيات اللازمة لتحديد أي نقطة في داخله.^[1]^[2] وهذه الخطوط لها بعدا واحدا لأن إحداثي واحد فقط هو المطلوب لتحديد النقطة عليه (على سبيل المثال، النقطة عند العدد 5 على خط الأعداد). للسطوح مثل المستوى أو سطح الأسطوانة أو الكرة لها بعدين لأنه لابد من وجود إحداثيين لتحديد نقطة عليه (على سبيل المثال، لتحديد موقع نقطة على سطح كرة نحتاج إلى خط العرض و خط الطول لتلك النقطة). داخل المكعب أو الأسطوانة أو الكرة فإن الأبعاد تكون ثلاثية لأن المطلوب ثلاثة إحداثيات لتحديد نقطة ضمن هذا المكان.

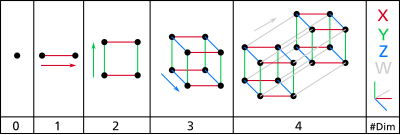من اليسار إلى اليمين مربع، مكعب وتسراكت. يحاط المربع بخط ذو بعد واحد، المكعب بمساحة ذات بعدين، والتسراكت بحجم ذو 3 أبعاد.

يعرض الرسم البياني أول أربعة أبعاد مكانية.1-D: نقطتين A و B يمكن توصيل خط، لإعطاء قطعة مستقيمة جديدة تسمى AB.2-D: قطعتين مستقيمتين موازييتين AB و CD ويمكن توصيلهما لتكوين مربع، مع زوايا معلمة ABCD.3-D: مربعين متوازييين ABCD و EFGH يمكن توصيلهما لتكوين مكعب، مع زوايا معلمة ABCDEFGH.4-D: مكعبين متوازييين ABCDEFGH و IJKLMNOP ويمكن توصيلهما لتكوين مكعب فائق رباعي الأبعاد، مع زوايا معلمة ABCDEFGHIJKLMNOP.

في الفيزياء[عدل]

الأبعاد المكانية[عدل]

عدد الأبعاد

أمثلة لنظام الإحداثيات

مستقيم الأعداد	زاوية

ديكارتي (بعدين)	قطبي	خط طول وخط عرض

ديكارتي (3 أبعاد)	أسطواني	كروي

مراجع[عدل]

^ "Curious About Astronomy"، Curious.astro.cornell.edu، مؤرشف من الأصل في 24 يناير 2015، اطلع عليه بتاريخ 03 مارس 2014.
^ "MathWorld: Dimension"، Mathworld.wolfram.com، 27 فبراير 2014، مؤرشف من الأصل في 24 أكتوبر 2018، اطلع عليه بتاريخ 03 مارس 2014.

في كومنز صور وملفات عن: بعد

ع ن ت الأبعاد
المكانات البُعدية	المكان المتجهي المكان الإقليدي المكان التآلفي المكان الإسقاطي Free module متعدد الشعب التنوع الجبري الزمكان
أبعاد أخرى	كرول Lebesgue covering Inductive هاوسدورف مينكوفسكي كسيري درجات الحرية
متعددات مقام وأشكال	المستو الفائق السطح الفائق مكعب زائدي ^{[لغات أخرى]} هايبرسفير مستطيل زائدي ^{[لغات أخرى]} Demihypercube Cross-polytope مهيكل ^{[لغات أخرى]}
الأبعاد حسب العدد	الصفري الأحادي الثنائي الثلاثي الرباعي الخماسي السداسي السباعي الثماني التساعي سلبي الأبعاد
التصنيف

هذه بذرة مقالة عن الفيزياء أو موضوع فيزيائي بحاجة للتوسيع. فضلًا شارك في تحريرها.

الهندسة الرياضية
جزء من سلسلة مقالات حول

الخطوط العريضة ^{[الإنجليزية]} التاريخ
الفروع إقليدية لاإقليدية إهليلجية كروية زائدية لا أرخميدية ^{[الإنجليزية]} إسقاطية نسبية تركيبية تحليلية جبرية حسابية ديوفانية ^{[الإنجليزية]} تفاضلية ريمانية هندسة تماسكية عقدية منتهية متقطعة رياضية رقمية محدبة رياضية حاسوبية وقعية ^{[الإنجليزية]}
المبادئ الخواص بعد الإنشاء بالمسطرة والفرجار زاوية منحنى ضلع قطري تعامد رياضي (تعامد هندسي) تواز رأس تطابق تشابه تناظر
صفري الأبعاد نقطة
وحيد البعد الطول مستقيم قطعة مستقيمة
المُسطَّحات مستو مساحة مضلع المثلثات مثلث الارتفاع الوتر مبرهنة فيثاغورس متوازيات الأضلاع متوازي أضلاع مربع مستطيل معين شبه معين رباعيات الأضلاع رباعي أضلاع شبه منحرف طائرة ورقية المنحنيات دائرة القطر المحيط المساحة قطع ناقص
المُجسَّمات حجم مكعب متوازي مستطيلات أسطوانة هرم كرة
ما فوق البعد الثالث مكعب رباعي الأبعاد كرة نونية الأبعاد
علماء الهندسة
وفق الاسم أيدا أريابهاتا أحمس ^{[الإنجليزية]} ابن الهيثم أبلونيوس أرخميدس عطية بولياي براهماغوبتا كارتن كوكستر ديكارت إقليدس أويلر غاوس غروموف هيلبرت جيهاديفا ^{[الإنجليزية]} كاتيايانا الخيَّام كلاين لوباتشيفسكي مانافا ^{[الإنجليزية]} مينكوفسكي مينغاتو ^{[الإنجليزية]} باسكال فيثاغورس باراميشفارا ^{[الإنجليزية]} بوانكاريه برنارد ريمان سكابي ^{[الإنجليزية]} السجزي الطوسي فيبلين ^{[الإنجليزية]} فيراسينا ^{[الإنجليزية]} يانغ هوي ^{[الإنجليزية]} ابن الياسمين زانج قائمة علماء الهندسة
وفق الحقبة قبل الميلاد أحمس ^{[الإنجليزية]} مانافا ^{[الإنجليزية]} فيثاغورس إقليدس أرخميدس أبلونيوس 1–1400م زانج كاتيايانا أريابهاتا براهماغوبتا فيراسينا ^{[الإنجليزية]} ابن الهيثم السجزي الخيَّام ابن الياسمين الطوسي يانغ هوي ^{[الإنجليزية]} باراميشفارا ^{[الإنجليزية]} 1400–1700م جيهاديفا ^{[الإنجليزية]} ديكارت باسكال مينغاتو ^{[الإنجليزية]} أويلر سكابي ^{[الإنجليزية]} أيدا 1700–1900م غاوس لوباتشيفسكي بولياي برنارد ريمان كلاين بوانكاريه هيلبرت مينكوفسكي كارتن فيبلين ^{[الإنجليزية]} كوكستر معاصرون عطية غروموف
بوابة هندسة رياضية
ع ن ت

في الفيزياء[عدل]

الأبعاد المكانية[عدل]

مراجع[عدل]

قائمة التصفح

بحث