مستخدم:Michel Bakni/ملعب4

الاشتقاق والمكاملة

المقالات الرئيسة: تفاضل الدوال المثلثية وقائمة تكاملات الدوال المثلثية وقائمة تكاملات الدوال المثلثية العكسية

المشتقات الأولى والثانية للدوال المثلثية مع مشتقاتها العكسية هي كما يلي:

دالة	مشتقها الأول	مشتقها الثاني	مشتقها من الرتبة n	تكامل
$\sin(x)$	$\cos(x)$	$-\sin(x)$	$\sin(x+{\frac {n\pi }{2}})$	$-\cos(x)$
$\cos(x)$	$-\sin(x)$	$-\cos(x)$	$\cos(x+{\frac {n\pi }{2}})$	$\sin(x)$
$\tan(x)$	$\sec ^{2}(x)$	$2\sec ^{2}(x).\tan(x)$	معقد	$-\ln |\cos(x)|$
$\cot(x)$	$-\csc ^{2}(x)$	$2\csc ^{2}(x).\cot(x)$	معقد	$\ln |\sin(x)|$
$\sec(x)$	$\sec(x).\tan(x)$	$\sec(x)(\sec ^{2}(x)+\tan ^{2}(x))$	معقد	$\ln |\sec(x)+\tan(x)|$
$\csc(x)$	$-\csc(x).\cot(x)$	$\csc(x)(\csc ^{2}(x)+\cot ^{2}(x))$	معقد	$-\ln |\csc(x)+\cot(x)|$

التعريف بواسطة التكامل

يمكن الحصول على تعريف آخر استنادا إلى الطول الدقيق لقوس الدائرة. باعتبار معادلة النصف العلوي لدائرة الوحدة $y={\sqrt {1-x^{2}}}$، يمكننا إيجاد العلاقة بين الزاوية $\theta$ و$\sin \theta$ وفقًا للمعادلة التالية:

$\int _{0}^{\sin \theta }{\sqrt {1+\left({d \over dx}{\sqrt {1-x^{2}}}\right)^{2}}}dx=\int _{0}^{\sin \theta }{\frac {dx}{\sqrt {1-x^{2}}}}=\theta$

حيث تنتمي الزاوية θ إلى المجال $0\leq \theta \leq \pi /2$.

التعريف بواسطة المعادلات التفاضلية

• الجيب وجيب التمام هما من الدوال الفريدة من نوعها التي تقبل التفاضل، بحيث:

${\begin{aligned}{\frac {d}{dx}}\sin x&=\cos x,\\{\frac {d}{dx}}\cos x&=-\sin x,\\\sin 0&=0,\\\cos 0&=1.\end{aligned}}$

كل من دالتي الجيب والجيب التمام تحققان المعادلة التفاضلية التالية: $y''=-y$ (معادلتها المميزة هي $m^{2}+1=0$، جذرها هي وحدة تخيلية موجبة أو سالبة ±i) بتعبير آخر، كل منهما تساوي مقابل مشتقتها من الدرجة الثانية.

الجيب هو الحل الوحيد لهذه المعادلة التي تحقق الشروط التالية:

${\begin{cases}y(0)=0\\[2pt]y\,'(0)=1\end{cases}}$

جيب التمام هو الحل الوحيد لهذه المعادلة التي تحقق الشروط التالية:

${\begin{cases}y(0)=1\\[2pt]y\,'(0)=0\end{cases}}$

بتطبيق قاعدة ناتج القسمة على تعريف ظل الزاوية باعتباره نسبة بين الجيب وجيب التمام، يحصل الفرد على أن دالة الظل تحقق:

${\frac {d}{dx}}\tan x=1+\tan ^{2}x.$

إذن، دالة الظل هي حل للمعادلة التفاضلية التالية:

$y'=1+y^{2}$

• نعتبر المعادلة التفاضلية من الدرجة الثانية التالية: $ay''+by'+cy=0$

إن حل هذه المعادلة هي الدالة الأسية من الشكل $y=A_{1}e^{m_{1}x}+A_{2}e^{m_{2}x}$، حيث $m_{1}$ و $m_{2}$ هما جذور المعادلة المميزة للمعادلة ($am^{2}+bm+c=0$). أيضا $A_{1}$ و $A_{2}$ هي ثوابت كيفية بناءً على الشروط الأولية.

إذا كانت المعادلة المميزة لها جذور عقدية، فإن حل هذه المعادلة هي الدالة الأسية العقدية:

$y=A_{1}.e^{(\alpha +i\beta )x}+A_{2}.e^{(\alpha -i\beta )x}$

حيث $\alpha$ هو الجزء الحقيقي و $\beta$ هو الجزء التخيلي لجذر المعادلة المميزة. استنادًا إلى صيغة أويلر، يمكننا تحويل الدالة الأسية العقدية إلى دالتي الجيب وجيب التمام، لذلك في حالة الجذور العقدية، ستتضمن حل المعادلة التفاضلية دوال مثلثية:

$y=A_{1}.e^{\alpha x}\cos \beta x+A_{2}.e^{\alpha x}\sin \beta x$

باستعمال المتسلسلات

دالة الجيب (باللون الأزرق) تحسب بصفة تقريبية اقترابا كبيرا بواسطة متعددة الحدود لتايلور من الدرجة السابعة (باللون الوردي) بالنسبة لدورة كاملة متمركزة حول أصل المَعلم.

الرسوم المتحركة لتقريب جيب التمام بواسطة متعددة الحدود لتايلور.

$\cos(x)$ إلى جانب متعددات الحدود الأولى لتايلور $p_{n}(x)=\sum _{k=0}^{n}(-1)^{k}{\frac {x^{2k}}{(2k)!}}$

دوال مثلثية هي دوال تحليلية. يمكن تمثيل جميع الدوال المثلثية بواسطة متسلسلات لانهائية.

باستخدام متسلسلة تايلور، يمكن كتابة كل دالة مستمرة على شكل متسلسلة قوة بجوار النقطة a على النحو التالي:

$f(x)=f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f'''(a)}{3!}}(x-a)^{3}+\cdots$

حيث تشير n! إلى عاملي عدد.

عندما يكون a=0، تتحول هذه المتسلسلة إلى متسلسلة ماكلورين، رياضيا:

$f(x)=f(0)+{\frac {f'(0)}{1!}}x+{\frac {f''(0)}{2!}}x^{2}+{\frac {f^{(3)}(0)}{3!}}x^{3}+\cdots$

ملاحظة: الزاوية x مقاسة بالتقدير الدائري في جميع السلاسل التالية.

متسلسلتا ماكلورين لدالتي الجيب وجيب التمام

• جيب الزاوية:

يوضح الشكل المقابل الرسم البياني لدالة الجيب إلى جانب متعدد الحدود السابع لماكلورين. قيمة دالة الجيب عند الصفر تساوي صفر، لذا فإن الحدود الزوجية لمتسلسلة القوة للجيب هي صفر. ونتيجة لذلك، فإن متسلسلة القوة للجيب ستحتوي فقط على حدود فردية.

${\begin{aligned}\sin x&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\[8pt]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1},\\[8pt]\end{aligned}}$

• جيب تمام الزاوية

وبالمثل، فإن الحدود الفردية لمتسلسلة جيب التمام هي صفر ، وتحتوي المتسلسلة فقط على حدود زوجية.

${\begin{aligned}\cos x&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.\end{aligned}}$

نصف قطر التقارب لتلك المتسلسلات غير منتهية. ولذلك، يمكن أن تمدد دالتا الجيب وجيب التمام إلى دوال صحيحة، والتي هي (بالتعريف) دوال ذات قيم عقدية وهولومورفية على مجمل المستوي العقدي.

متسلسلات القوى لباقي الدوال

الدوال المثلثية الأخرى لها مجالات خاصة، لذلك لا يمكن تحديد متسلسلة تايلور لأي قيمة. بالنسبة لدالتي الظل والقاطع غير المعرفة عند π/2 (أو °90)، تكون مجال تعريف متسلسلاتهم بين -π/2 و π/2، لذا، يمكن تمثيل هاتين الدالتين بواسطة متسلسلة ماكلورين. أيضًا بالنسبة لدالتي ظل التمام وقاطع التمام غير المعرفة عند الصفر، تكون مجال تعريف متسلسلاتهم بين 0 و π وبين -π و 0، لذلك، يمكن تمثيلهن بواسطة متسلسلة لوران، هذه الأخيرة، هي تمثيل دالة على شكل متسلسلة القوى ذات درجات سالبة (متسلسلة ذات بعض الحدود المرفوعة لِأُس سالب).

بتعبير أدق، نعرف:

U_n، هو عدد Up/down من الرتبة n.

B_n، هو عدد بيرنولي من الرتبة n.

و E_n، هو عدد أويلر من الرتبة n.

${\begin{aligned}\tan x&=\sum _{n=0}^{\infty }{\frac {U_{2n+1}x^{2n+1}}{(2n+1)!}}\\&=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}=x+{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}+{\frac {17}{315}}x^{7}+\cdots ,\qquad {\text{for }}|x|<{\frac {\pi }{2}}\\\cot x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}=x^{-1}-{\frac {1}{3}}x-{\frac {1}{45}}x^{3}-{\frac {2}{945}}x^{5}-\cdots ,\qquad {\text{for }}0<|x|<\pi \\\sec x&=\sum _{n=0}^{\infty }{\frac {U_{2n}x^{2n}}{(2n)!}}\\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}x^{2n}}{(2n)!}}=1+{\frac {1}{2}}x^{2}+{\frac {5}{24}}x^{4}+{\frac {61}{720}}x^{6}+\cdots ,\qquad {\text{for }}|x|<{\frac {\pi }{2}}\\\csc x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}}=x^{-1}+{\frac {1}{6}}x+{\frac {7}{360}}x^{3}+{\frac {31}{15120}}x^{5}+\cdots ,\qquad {\text{for }}0<|x|<\pi \end{aligned}}$

تُعرف الدوال المثلثية الأربعة الأخيرة على أنها كسور من الدوال الصحيحة. ولذلك، يمكن أن تُمدّد إلى دوال ميرومورفية، والتي هي دوال هولومورفية في كامل المستوي العقدي، باستثناء بعض النقاط المعزولة التي تسمى الأقطاب. هنا، الأقطاب هي أعداد من الشكل ${\textstyle (2k+1){\frac {\pi }{2}}}$ بالنسبة لدالتي الظل والقاطع، أو $k\pi$ بالنسبة لدالتي ظل التمام وقاطع التمام، حيث k هو عدد صحيح كيفي.

يمكن أيضًا حساب علاقات الاستدعاء الذاتي لمعاملات متسلسلة تايلور لتلك الدوال. متسلسلاتهما لها نصف قطر التقارب منتهي. معاملاتهم لها تفسير توافقي: فهي تُعدّد التبديلات المتناوبة للمجموعات المنتهية.

عدد الحدود في متسلسلة القوة المستخدمة لتقريب الدوال غير منتهي، ولكن في الحسابات يتم استخدام عدد محدود من تلك الحدود. يطلق على الحدود الأخرى غير المحسوبة اسم الباقي. يُعرَّف الباقي من الرتبة n لمتسلسلة بواسطة:

$R_{n}(x)={\frac {f^{(n+1)}(c)}{(n+1)!}}(x-a)^{n+1},a<c<x$

مع زيادة قيمة x، ستكون هناك حاجة إلى المزيد من الحدود لتحقيق دقة معينة، ونتيجة لذلك، ستنخفض سرعة التقارب. بالإضافة إلى ذلك، فإن الدوال الأربعة الأخيرة لها نقاط عدم الاستمرار (نقاط عدم الإتصال)، ومتسلسلات القوى لهذه الدوال معرفة على مجال معين.

لمنع التقارب من التباطؤ والتخلص من مشكلة نقاط عدم الاستمرار، يجب علينا تقليص الزاوية قدر الإمكان قبل استخدام المتسلسلة. باستخدام متطابقات الزوايا المتتامة، يمكن تقليص الزاوية إلى $(0,{\tfrac {\pi }{4}})$، وباستخدام بعض المتطابقات المثلثية إلى $(0,{\tfrac {\pi }{2}})$. بهذه الطريقة، تزداد سرعة تقارب المتسلسلة والكفاءة الحسابية.

متسلسلات أخرى

هناك تمثيل متسلسلات مفكوكًا كسريًّا جزئيًّا، حيث يتم جمع دوال المقلوب المزاحة فقط، بحيث تتطابق أقطاب دالة ظل التمام ودوال المقلوب:

$\pi \cot(\pi x)=\lim _{N\to \infty }\sum _{n=-N}^{N}{\frac {1}{x+n}}={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2x}{x^{2}-n^{2}}}.$

يمكن إثبات هذه المتطابقة بواسطة حيلة هيرغلوتس .

وبنفس الطريقة، يمكننا إيجاد المفكوكات الكسرية الجزئية لكل من القاطع وقاطع التمام والظل:

${\frac {\pi }{\sin \pi x}}={\frac {1}{x}}+2x\sum _{n=1}^{\infty }{\frac {(-1)^{n}}{x^{2}-n^{2}}},$

${\frac {\pi }{\cos \pi x}}=\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n+1)}{(n+{\tfrac {1}{2}})^{2}-x^{2}}},$

$\pi \tan {\frac {\pi x}{2}}=\sum _{n=0}^{\infty }{\frac {4x}{(2n+1)^{2}-x^{2}}}.$

الكسور المستمرة المعممة

طالع أيضًا: كسر مستمر معمم

كسر مستمر معمم هو تعميم للكسور المستمرة الاعتيادية حيث تأخذ مقاماته وبسوطه قِيَمًا حقيقية أو عقدية ما.

يمكننا كتابة الدوال الرياضية على هذا النحو:

$a_{0}+a_{0}a_{1}+a_{0}a_{1}a_{2}+\cdots +a_{0}a_{1}a_{2}\cdots a_{n}={\cfrac {a_{0}}{1-{\cfrac {a_{1}}{1+a_{1}-{\cfrac {a_{2}}{1+a_{2}-{\cfrac {\ddots }{\ddots {\cfrac {a_{n-1}}{1+a_{n-1}-{\cfrac {a_{n}}{1+a_{n}}}}}}}}}}}}}\,$

فيما يلي الكسور المستمرة لبعض الدوال:

${\begin{aligned}\sin x={\cfrac {x}{1+{\cfrac {x^{2}}{2\cdot 3-x^{2}+{\cfrac {2\cdot 3x^{2}}{4\cdot 5-x^{2}+{\cfrac {4\cdot 5x^{2}}{6\cdot 7-x^{2}+\ddots }}}}}}}},&&&&&&&&&\cos x={\cfrac {1}{1+{\cfrac {x^{2}}{2-x^{2}+{\cfrac {2x^{2}}{3\cdot 4-x^{2}+{\cfrac {3\cdot 4x^{2}}{5\cdot 6-x^{2}+\ddots }}}}}}}}\end{aligned}}$

${\begin{aligned}\tan x={\cfrac {x}{1-{\cfrac {x^{2}}{3-{\cfrac {x^{2}}{5-{\cfrac {x^{2}}{7-\dots }}}}}}}}={\cfrac {1}{{\cfrac {1}{x}}-{\cfrac {1}{{\cfrac {3}{x}}-{\cfrac {1}{{\cfrac {5}{x}}-{\cfrac {1}{{\cfrac {7}{x}}-\dots }}}}}}}},&&&&&&\cot x={\cfrac {1}{x}}-{\cfrac {x}{3-{\cfrac {x^{2}}{5-{\cfrac {x^{2}}{7-{\cfrac {x^{2}}{9-\dots }}}}}}}}\end{aligned}}$

متسلسلة الجداء اللانهائي

الجداء اللانهائي التالي لدالة الجيب له أهمية كبيرة في التحليل العقدي:

$\sin z=z\displaystyle \prod _{n=1}^{\infty }\left(1-{\frac {z^{2}}{n^{2}\pi ^{2}}}\right),\quad z\in \mathbb {C} .$

من هذه المتسلسلة، نستنتج أن:

$\cos z=\displaystyle \prod _{n=1}^{\infty }\left(1-{\frac {z^{2}}{\left(n-{\frac {1}{2}}\right)^{2}\pi ^{2}}}\right),\quad z\in \mathbb {C} .$

باستخدام المعادلات الدالية

يمكننا أيضا تعريف الدوال المثلثية باستخدام المعادلات الدالية المختلفة.

مثلا، الجيب وجيب التمام هما دالتان فريدتان من الدوال المستمرة التي تحقق صيغة الفرق:

$\cos(x-y)=\cos x\cos y+\sin x\sin y\,$

بشرط أن تكون $0<x\cos x<\sin x<x$ من أجل $0<x<1$.

في المستوى العقدي

طالع أيضًا: تحليل عقدي

يمكن التعبير عن الجيب وجيب التمام لعدد عقدي بدلالة الدوال نفسها والدوال الزائدية:

${\begin{aligned}\sin(x+iy)&=\sin x\cosh y+i\cos x\sinh y\\[5pt]\cos(x+iy)&=\cos x\cosh y-i\sin x\sinh y\end{aligned}}$

من الممكن أن نمثل بيانيا الدوال المثلثية دوالا ذات قيم عقدية عن طريق تمثيل بواسطة الألوان. يمكن مشاهدة العديد من الميزات الفريدة للدوال العقدية من الرسم البياني؛ على سبيل المثال، يمكن اعتبار دالتي الجيب وجيب التمام أنهما غير منتهية عندما يصبح الجزء التخيلي لـ z أكبر (لأن اللون الأبيض يمثل اللانهاية)، وحقيقة أن الدوال تحتوي على أصفار أو أقطاب بسيطة تتضح من حقيقة أن الألوان تدور حول كل صفر أو قطب مرة واحدة بالضبط. إن مقارنة هذه التمثيلات البيانية (بواسطة الألوان) مع تلك التمثيلات الخاصة بالدوال الزائدية توضح العلاقات بينهما.

تمثيل الدوال على المستوى العقدي:

$\sin z\,$	$\cos z\,$	$\tan z\,$	$\cot z\,$	$\sec z\,$	$\csc z\,$	التمثيل البياني لـ z=x+iy الذي استخدم في التمثيلات البيانية.

حيث تمثل العمدة بالألوان، والمعيار بوسائل أخرى، مثل السطوع أو الاشباع اللوني.

الخصائص

زوجية وفردية

المقالة الرئيسة: دوال زوجية وفردية

الدوال الزوجية والدوال الفردية هي دوال تحقق شرطا معينا يتعلق بالتناظر.

جيب التمام والقاطع دالتان زوجيتان، أما الدوال الأخرى فهي دوال فردية، بتعبير آخر:

${\begin{aligned}\sin(-x)&=-\sin x\\\cos(-x)&=\cos x\\\tan(-x)&=-\tan x\\\cot(-x)&=-\cot x\\\csc(-x)&=-\csc x\\\sec(-x)&=\sec x.\end{aligned}}$

دورية

المقالة الرئيسة: دالة دورية

الدوال المثلثية كلها دوالٌ دوريةٌ أصغر دور لها هو 2π. باستثناء الظل وظل التمام، التي أصغر دور لها هو π، بتعبير آخر، من أجل عدد صحيح k، لدينا:

${\begin{aligned}\sin(x+2k\pi )&=\sin x\\\cos(x+2k\pi )&=\cos x\\\tan(x+k\pi )&=\tan x\\\cot(x+k\pi )&=\cot x\\\csc(x+2k\pi )&=\csc x\\\sec(x+2k\pi )&=\sec x.\end{aligned}}$

في تحويل فورييه والمعادلات الموجية، تستخدم خاصية دورية الدوال المثلثية لحل المعادلات التفاضلية.

استمرارية (اتصال)

إن الجيب وجيب التمام هما دالتان مستمرتان دومٌا وقابلة للإشتقاق ويتضح ذلك بوضوح من خلال التعريف بواسطة المثلث القائم والتعريف بواسطة دائرة الوحدة. إن الدوال الأخرى، التي مقامهما هي دالة الجيب أو جيب التمام، ليست دائمًا مستمرة. لأن قيمة كل من دالة الجيب وجيب التمام في بعض الأماكن تساوي الصفر. نقاط عدم الاستمرار للدوال المثلثية هي كالتالي (حيث k هو عدد صحيح كيفي):

• الظل والقاطع: ${\pi \over 2}+k\pi$
• ظل التمام وقاطع التمام: $k\pi$

تعامد

تعتبر دالتا الجيب وجيب التمام دالتين متعامدتين، أي:

$\int _{0}^{2\pi }\cos n\theta \sin m\theta \,d\theta =0.$

${\frac {1}{\pi }}\int _{0}^{2\pi }\cos n\theta \cos m\theta \,d\theta =\left\{{\begin{array}{l l}0&\quad n\neq m\\1&\quad n=m\end{array}}\right.$

$\int _{0}^{2\pi }\sin m\theta \sin n\theta \,d\theta =0\quad (n\neq m).$

تستخدم هذه الخصائص لحساب معاملات متسلسلة فورييه.

تحويلا لابلاس وفورييه

تحويل لابلاس هو أحد طرق حل المعادلات التفاضلية. تحويلا لابلاس لدالتي الجيب وجيب التمام هي كما يلي:

• تحويل الجيب:

${\mathcal {L}}\{\sin(at)\}={\frac {a}{s^{2}+a^{2}}}$

• تحويل جيب التمام:

${\mathcal {L}}\{\cos(at)\}={\frac {s}{s^{2}+a^{2}}}$

تحويلا فورييه لدالتي الجيب وجيب التمام هي كما يلي:

• الجيب:

${\mathcal {F}}\{\sin(at)\}={\frac {\displaystyle \delta \left(\omega -{\frac {a}{2\pi }}\right)-\delta \left(\omega +{\frac {a}{2\pi }}\right)}{2i}}$

• جيب التمام:

${\mathcal {F}}\{\cos(at)\}={\frac {\delta \left(\omega -{\frac {a}{2\pi }}\right)+\delta \left(\omega +{\frac {a}{2\pi }}\right)}{2}}$

دالة ذاتية

إن دالتا الجيب وجيب التمام هما دالتان ذاتيتان لمؤثر لابلاس. على سبيل المثال، إذا كان : $\Delta =\nabla ^{2}$ يمثل مؤثر لابلاس أحادي البعد، فإن دالتا الجيب وجيب التمام تحقق : $\nabla ^{2}f=\lambda f$، حيث $\lambda$ هي قيمة ذاتية؛ يمكن التحقق من هذه المساواة انطلاقا من التعريف بواسطة المعادلة التفاضلية للدالتين.

حساب القيم

المقالة الرئيسة: جداول مثلثية

حساب القيم الدقيقة للدوال المثلثية يدوياً أمر صعب ومعقد، لكن في العصرِ الحديثِ، زالَت تعقيداته بسبب توفر أجهزة الحاسوب والآلات الحاسبة، التي تمكن بسهولة الحصول على القيمة الدقيقة لأي زاوية. بالنسبةِ لبعضِ الزوايا، فيمكن الحصول على القيم الجبرية الدقيقة لدوالِّها المثلثية دون اللجوء إلى حساباتٍ بالأجهزة، وتُسمّى هذه الزوايا: الزوايا الخاصة. على سبيل المثال، قيمُ الدوال المثلثية لجميع الزوايا من مضاعفات العدد 3 دقيقة. تُحسَبُ النسب المثلثية للزاوية 3° بتطبيق الفرق بين زاويتين ذات القيم 18° و15° (3 = 15 - 18). وتُحسَبُ النسب المثلثية للزاوية 18° باستخدام خواص ونِسَب الخماسي المنتظم.

لحساب قيمة دالة لأي زاوية، يجب على المرء أولاً تقليص مجال الزاوية (على سبيل المثال، من الصفر إلى π/2). يتم ذلك باستخدام كل من خاصية دورية وتناظر الدوال المثلثية.

قبل الحواسيب، حصل الناس بشكل عام على قيمة الدوال المثلثية من خلال استيفاء الجداول المثلثية. هذه الجداول لها تاريخ طويل في علم المثلثات. عادة ما يتم الحصول على القيم في الجداول عن طريق استخدام متطابقات نصف الزاوية وضعف الزاوية، على التوالي، بدءاً بقيمة معروفة (مثل sin (π/2) = 1).

تستخدم الحواسيب والحاسبات الحديثة مجموعةً متنوعةً من التقنياتِ لتوفير قيم الدوال المثلثية عند الطلب للزوايا الأخرى. تتمثل إحدى الطرق الشائعة، خاصةً في المعالِجات الراقية ذات وحدات الفاصلة العائمة، في جمع بين تقريب بواسطة كثير الحدود أو بواسطة الدوال الكسرية (مثل تقريب تشيبيشيف، تقريب بادي، وعادةً ما يتعلق بالدقة العليا أو المتغيرة، متسلسلات تايلور ومتسلسلة لوران) وتقليص المدى والبحث في الجدول—تبحث (الخوارزميات) أولاً في جدول صغير عن أقرب زاوية، ثم تستخدم كثير الحدود لحساب التصحيح. على الأجهزة الأكثر بساطة التي تفتقر إلى مضاعف العتاد، توجد خوارزمية تسمى CORDIC عالية الكفاءة، لأنها تَستَخدِم الإزاحات والإضافة والطرح فقط.

بالنسبة لحسابات عالية الدقة، عندما يصبح تقارب المتسلسلة بطيئًا للغاية، يمكن تقريب الدوال المثلثية بواسطة المتوسط الحسابي الهندسي، الذي يقارب في حد ذاته الدالة المثلثية بواسطة تكامل إهليلجي (عقدي).

متطابقات أساسية ومبرهنات

طالع أيضًا: قائمة المطابقات المثلثية

هناك عدد من المتطابقات تربط الدوال المثلثية بعضها ببعض. يحتوي هذا القسم على المتطابقات الأساسية والمبرهنات، لمزيد من المتطابقات، طالع قائمة المطابقات المثلثية. يمكن إثبات هذه المتطابقات هندسيا من التعريف باستعمال دائرة الوحدة أو التعريف باستعمال المثلث القائم (على الرغم من أنه بالنسبة للتعاريف الأخيرة، يجب توخي الحذر للزوايا التي لا تنتمي إلى هذا المجال [0 , π/2]). بالنسبة إلى البراهين غير الهندسية التي تستخدم فقط أدوات حساب التفاضل والتكامل، يمكننا استخدام المعادلات التفاضلية مباشرة. يمكننا أيضا استخدام متطابقة أويلر للتعبير عن جميع الدوال المثلثية بدلالة الدالة الأسية ذات القيم العقدية واستخدام خصائص الدالة الأسية.

متطابقة فيثاغورس

المقالة الرئيسة: متطابقة فيثاغورس المثلثية

تنص هذه المتطابقة على أن مجموع مربع جيب زاوية ما ومربع الجيب التمام لنفس الزاوية يساوي الواحد، ويُعبر عنها رياضياً بالعلاقة التالية:

$\sin ^{2}x+\cos ^{2}x=1,\,$

يجب الانتباه إلى أن التدوين sin² x + cos² x يكافئ sin x)² + (cos x)²).

متطابقات مجموع وفرق زاويتين

تسمح صيغ الفرع والمجموع بتوسيع الجيب وجيب التمام والظل لمجموع أو فرق زاويتين بدلالة جيب وجيب تمام وظل الزوايا نفسها.

المجموع

ويُحسب كما يأتي:

${\begin{aligned}\sin \left(x+y\right)&=\sin x\cos y+\cos x\sin y,\\\cos \left(x+y\right)&=\cos x\cos y-\sin x\sin y,\\\tan(x+y)&={\frac {\tan x+\tan y}{1-\tan x\tan y}}.\end{aligned}}$

الفرق

ويُحسب كما يأتي:

${\begin{aligned}\sin \left(x-y\right)&=\sin x\cos y-\cos x\sin y,\\\cos \left(x-y\right)&=\cos x\cos y+\sin x\sin y,\\\tan(x-y)&={\frac {\tan x-\tan y}{1+\tan x\tan y}}.\end{aligned}}$

متطابقات ضعف الزاوية

عندما تكون الزاويتان متساويتان، فإن صيغ المجموع تقلص إلى معادلات أبسط تعرف باسم متطابقات ضعف الزاوية.

${\begin{aligned}\sin 2x&=2\sin x\cos x={\frac {2\tan x}{1+\tan ^{2}x}},\\\cos 2x&=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x={\frac {1-\tan ^{2}x}{1+\tan ^{2}x}},\\\tan 2x&={\frac {2\tan x}{1-\tan ^{2}x}}.\end{aligned}}$

يمكن استخدام هذه المتطابقات لاشتقاق متطابقات تحويل المجموع إلى الجداء.

بوضع $\theta =2x$ و$t=\tan x,$ هذا يسمح بالتعبير عن جميع الدوال المثلثية لـ $\theta$ كدالة كسرية لـ ${\textstyle t=\tan {\frac {\theta }{2}}}$

${\begin{aligned}\sin \theta &={\frac {2t}{1+t^{2}}},\\\cos \theta &={\frac {1-t^{2}}{1+t^{2}}},\\\tan \theta &={\frac {2t}{1-t^{2}}}.\end{aligned}}$

بالإضافة إلى $d\theta ={\frac {2}{1+t^{2}}}\,dt$

هذا هو تعويض ظل نصف الزاوية (ويسمى أيضا تعويض فايرشتراس)، الذي يسمح بتقليص حساب التكاملات والمشتقات العكسية للدوال المثلثية إلى دوال كسرية.

متطابقات ثلاثية الزاوية

ويُحسب كما يأتي:

$\sin(3\theta )=3\sin \theta -4\sin ^{3}\theta =4\sin \theta \sin({\frac {\pi }{3}}-\theta )\sin({\frac {\pi }{3}}+\theta )$

$\cos(3\theta )=4\cos ^{3}\theta -3\cos \theta =4\cos \theta \cos({\frac {\pi }{3}}-\theta )\cos({\frac {\pi }{3}}+\theta )$

$\tan(3\theta )={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}=\tan \theta \tan({\frac {\pi }{3}}-\theta )\tan({\frac {\pi }{3}}+\theta )$

متطابقات نصف الزاوية

ويُحسب كما يأتي:

$\sin {\frac {\theta }{2}}=\pm {\sqrt {\frac {1-\cos \theta }{2}}}$

$\cos {\frac {\theta }{2}}=\pm {\sqrt {\frac {1+\cos \theta }{2}}}$

$\tan {\frac {\theta }{2}}=\pm {\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}={\frac {\sin \theta }{1+\cos \theta }}={\frac {1-\cos \theta }{\sin \theta }}=\csc \theta -\cot \theta$

قانون الجيب

ليكن ABC مثلث، وa وb وc أضلاعه، ينص قانون الجيب على ما يلي:

${\frac {\sin A}{a}}={\frac {\sin B}{b}}={\frac {\sin C}{c}}={\frac {2\Delta }{abc}}$

حيث تشير Δ إلى مساحة المثلث، أو بشكل مكافئ:

${\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R$

حيث يشير R إلى نصف قطر الدائرة المحيطة بالمثلث.

يمكن إثبات ذلك بتقسيم المثلث إلى مثلثين قائمين وباستخدام التعريف الوارد أعلاه للجيب. قانون الجيب مفيد في حساب أطوال الأضلاع المجهولة في مثلث إذا كانت هناك زاويتان وضلع واحد معلومتان. هذا هو الموقف الشائع الذي يحدث في التثليث، وهي تقنية لتحديد مسافات غير معروفة عن طريق قياس زاويتين ومسافة مغلقة يمكن الوصول إليها.

(3.أ) تمثيل المثلث الكروي ABC

في حالة المثلثات الكروية، ينص القانون على ما يلي:

${\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}$

حيث a و b و c هي أقواس المثلث الواقع في سطح الكرة (والتي يطلق عليها مجازًا أضلاع وتسمى أحيانًا جوانب المثلث الكروي)؛ و A و B و C هي الزوايا المقابلة.

قانون جيب التمام

(3.ب) طريقة الكاشي لبرهنة قانون جيب التمام بالنسبة للمثلثات الحادة (باستخدام مثلث حاد محاط بثلاث مربعات). حيث أن المستطيلين الأخضرين متقايسان والمستطيلين الأحمرين أيضًا متقايسان، يمكن إثبات تقايس المستطيلين الأخضرين بإثبات تقايس المثلثين JAE و JAB، والمثلثين JAB و CAM، والمثلثين CAM و FAM بتحريك أحد الرؤوس بالتوازي مع القاعدة وأحدهما بالدوران على أحد زوايا المربعات، ويمكن إثبات المستطيلين الأحمرين بطريقة مشابهة (انظر الصورة المتحركة)؛ ويمكن إثبات أن المستطيلين الأزرقين متقايسان ومساحة أحدهما يساوي CA × CB × cos C بمعرفة أن CE = CB cos C و CD = CA cos C. يمكن إثبات بالنسبة للمثلثات المنفرجة بطريقة مشابهة.

يعتبر قانون جيب التمام تعميمًا لمبرهنة فيثاغورس على جميع أنواع المثلثات المستوية. ويسمى أيضا مبرهنة الكاشي.

$c^{2}=a^{2}+b^{2}-2ab\cos C$

وقد تكتب هاته الصيغة كما يلي:

$\cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}$

حيث C هي الزاوية المقابلة للضلع c.

يمكن إثبات هذه المبرهنة بتقسيم المثلث إلى مثلثين قائمين وباستخدام مبرهنة فيثاغورس، أو باستخدام طريقة الكاشي المبينة في الشكل (3.ب).

يمكن استخدام قانون جيب التمام لحساب طول ضلع المثلث إذا كان الضلعان والزاوية بينهما معلومة. يمكن أيضًا استخدامه لإيجاد جيب تمام لأي زاوية إذا كانت أطوال كل الأضلاع معلومة.

في حالة المثلثات الكروية، ينص القانون على ما يلي:

$\cos c=\cos a\cos b+\sin a\sin b\cos C\,$

حيث a و b و c هي الأقواس الثلاثة للمثلث الكروي وتقاس بالدرجات القوسية أي بقيمة الزاوية المركزية المقابلة لكل منها داخل الكرة، حيث تحول بعد ذلك إلى وحدات الطول العادية بالضرب في قيمة الدرجة القوسية والتي تساوي محيط الكرة/360 ما يعادل ط × نصف قطر الكرة/180 والرمز ط هنا أو π في اللاتينية؛ والزاوية C هي الزاوية المقابلة للقوس c.

ويمكن اشتقاق المعادلة التالية مِن العلاقة السابقة لإيجاد قيمة الزاوية C المقابلة للقوس c في المثلث الكروي عندما تكون مجهولة وبقية الأطوال الثلاثة لأقواس المثلث a و b و c معلومة:

$\cos C\ ={\frac {\cos c-\cos a\cos b}{\sin a\sin b}}$

وهناك صورة أخرى للمعادلة حيث تكون قيم الزوايا الثلاث A و B و C معلومة لنحصل على قيمة قوس مجهول في المثلث الكُرويّ وليكن القوس c كما يلي:

$\cos c\ ={\frac {\cos C+\cos A\cos B}{\sin A\sin B}}$

ومنها يمكن حساب قيمة زاوية مجهولة بمعلومية طول القوس المقابل لها ومعلومية قيمتي الزاويتين الأخرتين بالمثلث الكروي هكذا:

$\cos C=\sin A\sin B\cos c\,-\cos A\cos B$

قانون الظل

المقالة الرئيسة: قانون الظل

ليكن ABC مثلث، تنص الأشكال الاربعة لقانون الظل على ما يلي:

${\frac {\tan {\frac {A-B}{2}}}{\tan {\frac {A+B}{2}}}}={\frac {a-b}{a+b}}\,;\qquad {\frac {\tan {\frac {A-C}{2}}}{\tan {\frac {A+C}{2}}}}={\frac {a-c}{a+c}}\,;\qquad {\frac {\tan {\frac {B-C}{2}}}{\tan {\frac {B+C}{2}}}}={\frac {b-c}{b+c}}.$

حيث A وB وC هي الزوايا المقابلة للأضلاع a وb وc على الترتيب.

يمكن إثبات هذه المبرهنة باستخدام قانون الجيب والمتطابقات المثلثية.

أما بالنسبة للمثلثات الكروية، ينص القانون على ما يلي:

${\frac {\tan \left({\dfrac {A-B}{2}}\right)}{\tan \left({\dfrac {A+B}{2}}\right)}}={\frac {\tan \left({\dfrac {a-b}{2}}\right)}{\tan \left({\dfrac {a+b}{2}}\right)}}.$

قانون ظل التمام

المقالة الرئيسة: قانون ظل التمام

(3.ج)

(3.د)

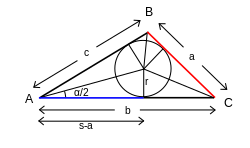
ليكن ABC مثلث، وa وb وc أضلاعه (حيث a=BC وb=AC وc=AB)، إذا كان:

$r={\sqrt {{\frac {1}{s}}(s-a)(s-b)(s-c)}}~$ (نصف قطر الدائرة الداخلية للمثلث)

و

$s={\frac {a+b+c}{2}}~$ (نصف محيط المثلث)،

ثم كل ما يلي يشكل قانون ظل التمام:

$\cot {\frac {A}{2}}={\frac {s-a}{r}}~;\qquad \cot {\frac {B}{2}}={\frac {s-b}{r}}~;\qquad \cot {\frac {C}{2}}={\frac {s-c}{r}}~.$

نستنتج أن:

${\frac {\cot {\dfrac {A}{2}}}{s-a}}={\frac {\cot {\dfrac {B}{2}}}{s-b}}={\frac {\cot {\dfrac {C}{2}}}{s-c}}={\frac {1}{r}}~.$

مبرهنة الساندويتش

طالع أيضًا: مبرهنة الساندويتش

تساعد هذه المبرهنة في حساب النهايات الصعبة ومشتقات الدوال المثلثية. هذه المتباينة الصالحة فقط عند المجال $-{\pi \over 2}<\theta <{\pi \over 2}$، هي كما يلي:

$\cos \theta <{\frac {\sin \theta }{\theta }}<1$

تمكننا هذه المتباينة من حساب النهاية التالية: $\lim _{x\to 0}{\frac {\sin x}{x}}$. تفيد هذه النهاية في حساب مشتقات الدوال المثلثية، طالع تفاضل الدوال المثلثية.

المتباينات المشابهة هي كما يلي:

${\frac {2}{\pi }}x\leq \sin x\leq x\qquad 0\leq x\leq {\frac {\pi }{2}}.$

$x\leq \tan x\qquad 0\leq x\leq {\frac {\pi }{2}}.$

$x<{\frac {\sin(\pi x)}{x(1-x)}}\leq 4\qquad 0\leq x\leq 1.$

مبرهنة بطليموس

المقالة الرئيسة: مبرهنة بطليموس

مبرهنة بطليموس هي علاقة بين الأضلاع الأربعة وقطرا الرباعي الدائري (رباعي محاط بدائرة تشمل جميع رؤوسه).

ليكن ABCD رباعي دائري، إذا كان θ₁+θ₂+θ₃+θ₄=180°، فإن:

${\begin{aligned}\sin(\theta _{1}+\theta _{2})\sin(\theta _{2}+\theta _{3})&=\sin(\theta _{2}+\theta _{3})\sin(\theta _{3}+\theta _{4})&{\text{(trivial)}}\\&=\sin(\theta _{3}+\theta _{4})\sin(\theta _{4}+\theta _{1})&{\text{(trivial)}}\\&=\sin(\theta _{4}+\theta _{1})\sin(\theta _{1}+\theta _{2})&{\text{(trivial)}}\\&=\sin \theta _{1}\sin \theta _{3}+\sin \theta _{2}\sin \theta _{4}.&{\text{(significant)}}\end{aligned}}$

صيغة مولفيده

المقالة الرئيسة: صيغة مولفيده

لتكن a و b و c أطوال أضلاع للمثلث، و α و β و γ الزوايا المقابلة لتلك الأضلاع الثلاثة على التوالي. تنص صيغة مولفيده على ما يلي:

${\frac {a+b}{c}}={\frac {\cos \left({\frac {\alpha -\beta }{2}}\right)}{\sin \left({\frac {\gamma }{2}}\right)}}$

${\frac {a-b}{c}}={\frac {\sin \left({\frac {\alpha -\beta }{2}}\right)}{\cos \left({\frac {\gamma }{2}}\right)}}$

قانون موري

ينص هذا القانون الرياضي على أن جداء جيوب التمام لكل من 20° و40° و80° يساوي 1/8، بتعبير رياضي:

$\cos(20^{\circ })\cdot \cos(40^{\circ })\cdot \cos(80^{\circ })={\frac {1}{8}}.$

وهي حالة خاصة للمتطابقة العامة:

$2^{n}\cdot \prod _{k=0}^{n-1}\cos(2^{k}\alpha )={\frac {\sin(2^{n}\alpha )}{\sin(\alpha )}}$

مع $n=3$ و $\alpha =20^{\circ }$.

هذه المتطابقة تثير الفضول، لأن، عند تعويض n و α للحد الثاني بتلك القيم، يحصل المرء على أن:

${\frac {\sin(160^{\circ })}{\sin(20^{\circ })}}={\frac {\sin(180^{\circ }-20^{\circ })}{\sin(20^{\circ })}}=1,$

بما أن:

$\sin(180^{\circ }-x)=\sin(x).$

هناك متطابقة مشابهة لهذه المتطابقة، وهي متعلقة بدالة الجيب:

$\sin(20^{\circ })\cdot \sin(40^{\circ })\cdot \sin(80^{\circ })={\frac {\sqrt {3}}{8}}.$

زيادة على ذلك، عند تقسيم المتطابقة الثانية على الأولى، تنتج متطابقة أخرى:

$\tan(20^{\circ })\cdot \tan(40^{\circ })\cdot \tan(80^{\circ })={\sqrt {3}}=\tan(60^{\circ }).$

الدوال العكسية

المقالة الرئيسة: دوال مثلثية عكسية

الدوال المثلثية دورية، وبذلك، هي ليست متباينة، وبالتالي ليس لديها دالة عكسية.  ومع ذلك، في كل مجال تكون فيه الدالة المثلثية رتيبة، يمكن للمرء تحديد دالة عكسية، بهذه الطريقة، تعرّف الدوال المثلثية العكسية كدوال متعددة القيم. لتعريف دالة عكسية حقيقية، يصير من الضروري تقليص مجال تعريفها إلى مجال تكون فيه الدالة رتيبة، حتى تكون الدوال المثلثية دوالا تقابلية. يعطى الاختيار الشائع لهذا المجال الذي يطلق عليه اسم «مجموعة القيم الرئيسية» في الجدول التالي. عادة ما يشار إلى الدوال المثلثية العكسية بالبادئة "arc" قبل اسم أو اختصار الدالة.

يوضح الجدول الآتي قائمة الدوال المثلثية العكسية مع ابراز كل من مجال تعريفهن ومشتقتهن.

الدالة	اسمها بالإنجليزية	التدوين	التعريف	مجال التعريف	المجال المقابل (مجموعة القيم الرئيسية)	المشتقة
قوس الجيب	Arcsine	$\arcsin x=y\,$	$\sin y=x\,$	$-1\leq x\leq 1\,$	$-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}\,$	${\frac {1}{\sqrt {1-x^{2}}}}$
قوس جيب التمام	Arccosine	$\arccos x=y\,$	$\cos y=x\,$	$-1\leq x\leq 1\,$	$0\leq y\leq \pi \,$	$-{\frac {1}{\sqrt {1-x^{2}}}}$
قوس الظل	Arctangent	$\arctan x=y\,$	$\tan y=x\,$	جميع الأعداد الحقيقية	$-{\frac {\pi }{2}}<y<{\frac {\pi }{2}}\,$	${\frac {1}{1+x^{2}}}$
قوس قاطع التمام	Arccosecant	$\operatorname {arccsc} x=y\,$	$\csc y=x\,$	$x\leq -1$ أو $x\geq 1$	$-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},y\neq 0\,$	${\frac {-1}{|x|\,{\sqrt {x^{2}-1}}}}$
قوس القاطع	Arcsecant	$\operatorname {arcsec} x=y\,$	$\sec y=x\,$	$x\leq -1$ أو $x\geq 1$	$0\leq y\leq \pi ,y\neq {\frac {\pi }{2}}\,$	${\frac {1}{|x|\,{\sqrt {x^{2}-1}}}}$
قوس ظل التمام	Arccotangent	$\operatorname {arccot} x=y\,$	$\cot y=x\,$	جميع الأعداد الحقيقية	$0<y<\pi \,$	$-{\frac {1}{1+x^{2}}}$

غالبًا ما تستخدم التدوينات sin^-1 و cos^-1... إلخ لـ arcsin و arccos ،... وهكذا. عند استخدام هذا التدوين، قد يؤدي هذا إلى الالتباس بين الدوال العكسية والمعاكيس الضربية.

يمنع التدوين بالبادئة "arc" مثل هذا الالتباس، على الرغم من أنه يمكن الخلط بين "arcsec" لـ arcsecant و لـ "arcsecond"(التي تعني «ثانية القوس»).

يُمكن للدوال المثلثية العكسية أن تعرف بواسطة المتسلسلات تماما كما هو الحال بالنسبة للدوال المثلثية. على سبيل المثال،

$\arcsin z=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \,.$

يمكن أيضًا التعبير عنها بدلالة اللوغاريتمات العقدية. طالع مقالة الدوال المثلثية العكسية لمزيد من التفاصيل.

الدوال الزائدية

المقالة الرئيسة: دوال زائدية

(4.أ) صورة متحركة للدوال المثلثية (الدائرية) والدوال الزائدية. باللون الأحمر، منحنى معادلته x² + y² = 1 (دائرة الوحدة)، وبالأزرق x² - y² = 1 (القطع الزائد)، مع النقاط (cos(θ),sin(θ)) و (1,tan(θ)) باللون الأحمر و (cosh(θ),sinh(θ)) و (1,tanh(θ)) باللون الأزرق.

الدوال الزائدية هي تلك الدوال التي تشبه الدوال المثلثية لكنها معرفة بواسطة القطع الزائد بدلاً من الدائرة: تمامًا كما تشكل النقاط (cos t, sin t) دائرة ذات نصف قطر يساوي الواحد، تشكل النقاط (cosh t, sinh t) النصف الأيمن للقطع الزائد.

الدوال الزائدية هي:

الدالة	التدوين	التعريف	المنطلق والمستقر	تعبير بدلالة الدوال المثلثية
الجيب الزائدي	$\sinh x$	${\frac {e^{x}-e^{-x}}{2}}$	$\mathbb {R} \rightarrow \mathbb {R}$	$-i\sin ix$
جيب التمام الزائدي	$\cosh x$	${\frac {e^{x}+e^{-x}}{2}}$	$\mathbb {R} \rightarrow [1,+\infty [$	$\cos ix$
الظل الزائدي	$\tanh x$	${\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$	$\mathbb {R} \rightarrow ]-1,1[$	$-i\tan ix$
ظل التمام الزائدي	$\coth x$	${\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}$	$\mathbb {R} ^{*}\rightarrow ]-\infty ,-1[\cup ]1,+\infty [$	$i\cot ix$
القاطع الزائدي	$\operatorname {sech} x$	${\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}$	$\mathbb {R} \rightarrow ]0,1]$	$\sec {ix}$
قاطع التمام الزائدي	$\operatorname {csch} x$	${\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}$	$\mathbb {R} ^{*}\rightarrow \mathbb {R} ^{*}$	$i\csc ix$

يعتمد كلا النوعين على عُمدة، إما زاوية دائرية أو زاوية زائدية.

بما أن مساحة القطاع الدائري الذي نصف قطره r وزاويته u هي ${\frac {1}{2}}r^{2}u$ ، فسوف تكون مساوية لـ u عندما تكون r = √2. في الرسم البياني، تكون الدائرة مماسية على القطع الزائد الذي معادلته xy = 1 عند النقطة (1,1). يمثل القطاع البرتقالي مساحة ومقدار الزاوية الدائرية. وبالمثل، تمثل القطاعان الأصفر والأحمر معًا مساحة ومقدار الزاوية الزائدية.

سيقان المثلثين القائمين اللذين وتراهما هما عبارة عن شعاع محدد للزوايا يبلغ طولهما 2√ مرة الدوال الدائرية والزائدية.

في حالة القطع الزائد الذي معادلته x² - y² =1، مقدار الزاوية الزائدية هو ضعف المساحة الزرقاء المحددة بنصف المستقيم ومحور السينات والقطع الزائد (انظر الصورة (4.ج))، تماما كما يكون مقدار الزاوية الدائرية هو ضعف المساحة الزرقاء للدائرة التي معادلتها x² + y² =1 (انظر الصورة (4.د)).

في المتطابقات الزائدية، هناك تشابه كبير بينها وبين المتطابقات المثلثية، بعض الأمثلة على ذلك:

$\sinh(x+y)=\sinh x\cosh y+\cosh x\sinh y$

$\cosh ^{2}x-\sinh ^{2}x=1$

$\cosh 2x=\cosh ^{2}x+\sinh ^{2}x$

$e^{x}=\cosh x+\sinh x$

هناك علاقة تربط الدوال المثلثية بالدوال الزائدية دون اللجوء إلى استخدام الأعداد العقدية تُعْرَف بالدالة الغودرمانية، وهي معرّفة من $\mathbb {R}$ نحو $\left]-{\frac {\pi }{2}},{\frac {\pi }{2}}\right[$ بـ:

${\begin{aligned}\operatorname {gd} x&=\int _{0}^{x}\operatorname {sech} t\,\mathrm {d} t=\arcsin \left(\tanh x\right)=\arctan(\sinh x)=\operatorname {arccsc} (\coth x)\\[6pt]&=\operatorname {sgn}(x)\arccos \left(\operatorname {sech} x\right)=\operatorname {sgn}(x)\operatorname {arcsec} (\cosh x)\\[6pt]&=2\arctan \left(\tanh {\frac {x}{2}}\right)\\[6pt]\end{aligned}}$

حيث $\operatorname {sgn}(x)$ هي دالة الإشارة.

• 
  (4.ب) الدائرة والقطع الزائد متلامسان عند النقطة (1,1) تعرضان هندسة الدوال الدائرية بدلالة مقدار الزاوية u، والدوال الزائدية اعتمادًا على مقدار الزاوية u.
• 
  (4.ج)
• 
  (4.د)

علاقة الدوال المثلثية بالدوال الخاصة

يمكن كتابة بعض الدوال الخاصة بدلالة مجموعة من الدوال بما في ذلك الدوال المثلثية.

• دالة بيسل من الرتبة 1/2: دالة بيسل التي هي عبارة عن متسلسلة القوى، هي حل للمعادلة التفاضلية من الدرجة الثانية التالية:

$x^{2}y''+xy'+(x^{2}-a^{2})y=0$

حيث يمثل a الرتبة. يمكن كتابة أحد الحالات الخاصة لدالة بيسل (a = 1/2) بدلالة الدوال المثلثية على النحو التالي:

$J_{1/2}={\sqrt {\frac {2}{\pi x}}}\sin x$

$J_{-1/2}={\sqrt {\frac {2}{\pi x}}}\cos x$

• متعدد الحدود لتشيبيشيف: هو الحل للمعادلة التفاضلية من الدرجة الثانية التالية:

$(1-x^{2})y''-xy'+n^{2}y=0$

حيث تمثل n رتبتها.

يمكن كتابة متعدد الحدود لتشيبيشيف من الرتبة n بدلالة الدوال المثلثية:

$T_{n}=\cos(n\arccos x)$

تطبيقات

حساب المتجهات

في الرياضيات والفيزياء، تُستخدم المتجهات (التي لها مقدار واتجاه) لتمثيل كمية متجهة وبالاخص في الفيزياء مثل تمثيل القوة والسرعة. تستخدم بعض حسابات المتجهات دوال مثلثية. على سبيل المثال، يمكن حساب الضرب النقطي لمتجهين x وy بواسطة قانون جيب التمام:

${\vec {x}}\cdot {\vec {y}}=\cos \left(\angle ({\vec {x}},{\vec {y}})\right)\ \cdot \parallel \!\!{\vec {x}}\!\!\parallel \cdot \parallel \!\!{\vec {y}}\parallel$

يمكن أيضًا استخدام المعادلة التالية لحساب مقدار الضرب المتجهي:

$\parallel {\vec {x}}\times {\vec {y}}\!\!\parallel =\sin \left(\angle ({\vec {x}},{\vec {y}})\right)\ \cdot \parallel \!\!{\vec {x}}\!\!\parallel \cdot \parallel \!\!{\vec {y}}\parallel$

الإحداثيات القطبية، والأسطوانية والكروية

(5.أ) تمثيل نقطتين في نظام الإحداثيات القطبية

الدوال المثلثية هي الأساس لتحديد نظام الإحداثيات القطبية الذي يكون فعالا في تبسيط العديد من المشكلات الرياضية والفيزيائية، بما في ذلك بعض التكاملات. في نظام الإحداثيات هذا، بدلاً من إحداثيات x وy لنقطة (المستخدمة في نظام الإحداثيات الديكارتية)، بُعدها عن المركز والزاوية المحصورة بين الخط الذي يربطها بالمركز والخط الأفقي (r , θ) فهي تعتبر إحداثيات النقطة. تحويل الإحداثيات الديكارتية إلى الإحداثيات القطبية والعكس بالعكس باستخدام الدوال المثلثية:

$x=r\cos \theta ,y=r\sin \theta$

تتشكل أيضًا أنظمة الإحداثيات الأسطوانية والكروية، التي تعد إحداثيات قطبية معممة على ثلاثية الأبعاد، على أساس الدوال المثلثية. تُستخدم هذه الأنظمة في مشكلات مثل تكاملات ثلاثية الأبعاد لها تناظر أسطواني أو كروي.

المساحات

• مثلث: هناك قانون يعبر عن مساحة المثلث بدلالة أضلاعه a وb والزاوية المحصورة بينهم θ دون الحاجة إلى معرفة ارتفاعه:

$S={1 \over 2}ab\sin \theta$

• متوازي أضلاع: يمكن ايجاد مساحته من خلال معرفة أطوال أضلاعه a وb وإحدى زواياه θ دون الحاجة إلى معرفة ارتفاعه بتطبيق هذا القانون:

$S=ab\sin \theta$

• مضلع منتظم: يمكن ايجاد مساحته من خلال تلك الصيغ:

${\frac {1}{4}}nl^{2}\cdot \cot(\pi /n)\ =\ {\frac {1}{4n}}p^{2}\cdot \cot(\pi /n)$

حيث n هو عدد أضلاعه، وl هو طول إحدى أضلاعه، وp هو محيط المضلع.

إذا كان المضلع محاط بدائرة نصف قطرها R ومحيط بدائرة نصف قطرها r (يُعتبَر أيضًا عامد المضلع):

${\frac {1}{2}}nR^{2}\cdot \sin(2\pi /n)\ =\ nr^{2}\tan(\pi /n)$

المحيطات

• مضلع منتظم: يمكن إيجاد محيطه بدلالة عدد أضلاعه n والمسافة بين مركز المضلع وأحد رؤوسه b ودالة الجيب:

$2nb\sin \left({\frac {\pi }{n}}\right)$

• قطع ناقص: يمكن إيجاد محيطه إنطلاقًا من نصف محوره الأكبر a والأصغر b باستخدام إحدى الدوال المثلثية:

$C\,=\,4a\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta \,=\,4a\,E(e)$

حيث $e={\sqrt {1-b^{2}/a^{2}}}$ هو معامل التباعد المركزي، و $E$ هو التكامل الإهليلجي التام من النوع الثاني:

$E(e)\,=\,\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta$

يتم الحصول على هذا القانون باستخدام صيغة حساب طول القوس والإحداثيات القطبية.

الحجوم

• متوازي السطوح: يمكن تعبير عن حجمه بدلالة جيب التمام:

$V=abc{\sqrt {1+2\cos(\alpha )\cos(\beta )\cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )}}$

حيث $\ \alpha =\angle ({\vec {b}},{\vec {c}}),\;\beta =\angle ({\vec {a}},{\vec {c}}),\;\gamma =\angle ({\vec {a}},{\vec {b}})$ ، و $a,b,c$ هي أطوال الأحرف.

علاقتها بالدالة الأسية وبالأعداد العقدية

(5.ب) تمثيل عدد عقدي على المستوي العقدي

• يمكن كتابة أي عدد عقدي على الشكل المثلثي:

$z=|z|(\cos \theta +i\sin \theta )$ حيث $|z|$ هو معيار العدد العقدي، و i هي وحدة تخيلية مربعها يساوي مقابل واحد ($i^{2}=-1$).

• يطلق على العلاقة بين الدالة الأسية والدوال المثلثية اسم صيغة أويلر:

$e^{i\theta }=\cos \theta +i\sin \theta$

إثبات: نعتبر متسلسلة تايلور للدالة الأسية:

$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {x^{5}}{5!}}+\cdots$

بوضع: $x=i\theta$، تصبح المتسلسلة:

$e^{i\theta }=1+i\theta -{\frac {\theta ^{2}}{2!}}-{\frac {i\theta ^{3}}{3!}}+{\frac {\theta ^{4}}{4!}}+{\frac {i\theta ^{5}}{5!}}-\cdots$

$e^{i\theta }=\left(1-{\frac {\theta ^{2}}{2!}}+{\frac {\theta ^{4}}{4!}}-\cdots \right)+i\left(\theta -{\frac {\theta ^{3}}{3!}}+{\frac {\theta ^{5}}{5!}}-\cdots \right)$

من متسلسلتا ماكلورين لدالتي الجيب وجيب التمام، نستنتج أن:

$e^{i\theta }=\cos \theta +i\sin \theta$

• لدينا:

${\begin{aligned}e^{i\theta }&=\cos \theta +i\sin \theta \\[5pt]e^{-i\theta }&=\cos \theta -i\sin \theta .\end{aligned}}$

قد تستعمل صيغة أويلر للحصول على بعض المتطابقات المثلثية، وذلك بكتابة دالتي الجيب والجيب التمام كما يلي:

$\sin \theta ={\frac {e^{i\theta }-e^{-i\theta }}{2i}}\;$

$\cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}\;$

• يمكن ملاحظة أن جيب التمام يمكن اعتباره الجزء الحقيقي والجيب هو الجزء التخيلي للدالة الأسية العقدية. رياضيا:

$\cos \theta =\operatorname {Re} (e^{i\theta })$

$\sin \theta =\operatorname {Im} (e^{i\theta })$

• يعرف الشكل المعمم لصيغة أويلر بصيغة دي موافر:

$e^{in\theta }=(\cos \theta +i\sin \theta )^{n}=\cos(n\theta )+i\sin(n\theta )$

• أيضًا، باستخدام تعريف بواسطة متسلسلة ماكلورين للدوال الزائدية والمثلثية، يمكن الحصول على العلاقات بين تلك الدوال:

$\sin z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}={\frac {e^{iz}-e^{-iz}}{2i}}={\frac {\sinh \left(iz\right)}{i}}$

$\cos z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}={\frac {e^{iz}+e^{-iz}}{2}}=\cosh \left(iz\right)$

علم الفلك

استخدمت حساب المثلثات الكروية لعدة قرون لتحديد موقع الشمس والاقمار والنجوم، والتنبؤ بالكسوف والخسوف، ووصف مدارات الكواكب.

في العصر الحديث، تستخدم تقنية التثليث في علم الفلك لقياس مسافة النجوم القريبة، وكذلك في أنظمة الملاحة عبر الأقمار الصناعية.

الخرائط والمساحة

(5.ج) تستخدم عملية التثليث في إيجاد إحداثيات والبعد لسفينة بالنسبة للشاطئ وذلك بقياس الزوايا بين نقطتين مرجعيتين

حساب المثلثات هو أساس معظم ممارسات رسم الخرائط والمساحة. قياس زاوية باستخدام الجهاز أو دون استخدامه، إسقاط الخرائط (تحويل سطح ناقصي إلى سطح مستوي)، وتحديد الارتفاعات، وحساب الاتجاه الزاوي، والمسح الاجتيازي المفتوح والمغلق، وتصميم الأقواس في إنشاء الطرقات، وتحويل ثنائي الأبعاد في المسح الجوي.

على سبيل المثال، في التثليث، وهي إحدى الطرق القديمة للمساحة، نحسب احداثيات نقطة معينة من خلال قياس الزوايا بين نقطتين مرجعيتين؛ يُستخدم هذا المبدأ حاليًا في القياس البصري ثلاثي الأبعاد . يُستخدَم في التثليث قانون جيب التمام وقانون الجيب لحساب زوايا المثلثات وتحديد الموقع الدقيق لكل نقطة.

في الحالة المبينة في الشكل (5.ج)، تُحسَب المسافة بتطبيق هذا القانون:

$d={\frac {\sin \alpha \,\sin \beta }{\sin(\alpha +\beta )}}\ell ={\frac {\tan \alpha \,\tan \beta }{\tan \alpha +\tan \beta }}\ell$

(5.د) رسم توضيحي لكيفية حساب ارتفاع جبل.

مثال آخر في التثليث، إذا أراد المرء قياس ارتفاع h لجبل أو مبنى مرتفع، يتم تحديد الزوايا α، و β من نقطتين أرضيتين إلى الأعلى (الشكل (5.د)). لتكن ℓ مسافة بين هذه النقاط، يحسب الارتفاع بتطبيق هذا القانون:

$h={\frac {\sin \alpha \,\sin \beta }{\sin(\beta -\alpha )}}\ell ={\frac {\tan \alpha \,\tan \beta }{\tan \beta -\tan \alpha }}\ell .$

متسلسلة فورييه وتحويل فورييه

دالتا الجيب وجيب التمام مثل كثيرات الحدود المتعامدة ولها استقلالية خطية. ومنهم يمكن كتابة أي دالة (دورية بشكل عام) على أنها العلاقة التالية بدلالة متسلسلة من تلك الدوال، والتي تسمى متسلسلة فورييه:

$f(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }(a_{n}\cos nx+b_{n}\sin nx)$

بالنسبة للدوال الفردية، فقط حدود دالة الجيب، أما الدوال الزوجية، فقط حدود دالة جيب التمام زائد معامل ثابت.

تحويل فورييه هو نوع من التحويل التكاملي وهو عبارة عن امتداد لمتسلسلة فورييه. يُعرف هذا التحويل بـ:

$F(\omega )={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{\infty }f(t)e^{-\mathrm {i} \omega t}\,dt$

تُحوّل الدالة الأسية العقدية إلى دوال مثلثية بواسطة صيغة أويلر. تستخدم تحويل فورييه لحل المعادلات التفاضلية الجزئية مثل معادلة الموجة والتحليل الطيفي ومعالجة الإشارات.

يستخدم تحويل جيب التمام المتقطع القريب من تحويل فورييه لتقليل حجم ملف JPEG أثناء التخزين مع الحفاظ على الجودة النسبية (ضغط الصور)، هذا التحويل هو تقنية تمثل البيانات على شكل مجاميع دوال جيب التمام.

الدوال الدورية

(5.هـ) صورة متحركة لموجة مربعية مع عدد متزايد من التوافقيات

الدوال المثلثية مهمة أيضا في الفيزياء. على سبيل المثال، يتم استخدام الجيب وجيب التمام لوصف الحركة التوافقية البسيطة، التي تنمذج العديد من الظواهر الطبيعية، مثل حركة كتلة متصلة بنابض، وبالنسبة للزوايا الصغيرة، الحركة الرقاصية لكتلة معلقة بواسطة خيط؛ وفي الكهرباء والإلكترونيات، تستخدم الدالتان الأخيرتان لدراسة الدارات الكهربائية مثل دارة مقاومة وملف ومكثف المهتزة. دوال الجيب وجيب التمام هي اسقاطات أحادية البعد لحركة دائرية منتظمة.

تثبت الدوال المثلثية أيضًا على أنها مفيدة في دراسة الدوال الدورية العامة. تُعد أنماط الموجات المميزة للدوال الدورية مفيدة لنمذجة الظواهر المتكررة مثل الصوت أو الموجات الضوئية.

بشكل عام، يمكن التعبير عن دالة دورية f(x) كمجموع موجات الجيب أو موجات جيب التمام في متسلسلات فورييه مثل موجة مربعة أو موجة سن المنشار.

نشير إلى الدالة التي تتضمن الجيب أو جيب التمام بـ φ_k، يأخذ مفكوك الدالة الدورية f(t) الشكل:

$f(t)=\sum _{k=1}^{\infty }c_{k}\varphi _{k}(t)$

حيث c_k هو معامل المتسلسلة.

على سبيل المثال، يمكن كتابة الموجة المربعية كمتسلسلة فورييه:

$f_{\text{square}}(t)={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\sin {\big (}(2k-1)t{\big )} \over 2k-1}.$

في الصورة المتحركة لموجة مربعية (5.هـ)، يمكن ملاحظة أن بعض الحدود فقط تنتج تقريبًا جيدًا إلى حد ما.

المنحنيات الوسيطية

طالع أيضًا: معادلة وسيطية

(5.و) منحنى ليساجو، كُوّن هذا الشكل باستعمال دوال تعتمد على الدوال المثلثية، حيث $\omega _{x}=5$ و $\omega _{y}=4$ ، و $a,b=1$ ، و $\delta ,\gamma =0$.

يمكن تمثيل بعض المنحنيات الخاصة باستخدام المعادلات الوسيطية وبدلالة الدوال المثلثية، بعض الأمثلة على المنحنيات الخاصة هي كما يلي:

• الدائرة: تعطى المعادلة الوسيطية للدائرة ذات المركز $(x_{0},y_{0})$ ونصف القطر $r$ بواسطة:

${\begin{cases}x=r\,\cos(t)+x_{0}\\y=r\,\sin(t)+y_{0}\end{cases}}$

• القطع الناقص: يُمثَّل القطع الناقص ذو المركز $(x_{0},y_{0})$ ونصف المحور الكبير $a$ ونصف المحور الصغير $b$ كما يلي:

${\begin{cases}x=a\,\cos(t)+x_{0}\\y=b\,\sin(t)+y_{0}\end{cases}}$

• منحنى ليساجو: تعطى الشكل الوسيطي لمنحنى ليساجو بواسطة:

${\begin{cases}x=a\,\sin(\omega _{x}t+\delta )\\y=b\,\sin(\omega _{y}t+\gamma )\end{cases}}$

حيث $\omega _{x}$ و $\omega _{y}$ هي عبارة عن ثوابت تصف عدد فصوص الشكل.

• القطع الزائد، يمكن تمثيل وسيطيًا القطع الزائد الأفقي بواسطة:

${\begin{cases}x=a\sec t+h\\y=b\tan t+k\end{cases}}$ أو ${\begin{cases}x=\pm a\cosh t+h\\y=b\sinh t+k\end{cases}}$

ويمكن تمثيل وسيطيًا القطع الزائد العمودي بواسطة:

${\begin{cases}x=a\tan t+h\\y=b\sec t+k\end{cases}}$ أو ${\begin{cases}x=a\sinh t+h\\y=\pm b\cosh t+k\end{cases}}$

حيث، $(h,k)$ هي مركز القطع الزائد.

بالإضافة إلى تلك المنحنيات، يمكن أيضًا تمثيل عدة رسومات التي تعتمد على الدوال المثلثية، بما في ذلك المنحنى العجلي التحتي، اللولب، السطوح الوسيطية ،... وهكذا.

البصريات

(5.ز) انكسار الضوء.

التطبيق الأساسي للدوال المثلثية في علم البصريات هو قانون سنيل. ينص هذا القانون، الذي ينطبق على ظاهرة انكسار الضوء، على العلاقة بين زوايا السقوط والانكسار:

${\frac {\sin \theta _{1}}{\sin \theta _{2}}}={\frac {v_{1}}{v_{2}}}={\frac {n_{2}}{n_{1}}}$

حيث:

• θ₁: زاوية سقوط الموجة، θ₂: زاوية انكسار الموجة.
• v₁: سرعة الضوء في الوسط الأول، v₂: سرعة الضوء في الوسط الثاني.
• n₁: معامل الانكسار للوسط الأول، n₂: معامل الانكسار للوسط الثاني

بالإضافة إلى انكسار الضوء، تُستخدم الدوال المثلثية في مجالات أخرى من البصريات، مثل تحليل تداخل الموجات والاستقطاب والحيود.

الملاحة 

طالع أيضًا: مسافة دائرة عظمى

(5.ح)

تاريخيا، استخدمت حساب المثلثات لتحديد احداثيات خطوط الطول والعرض لسفن الإبحار، ورسم المسارات، وحساب المسافات أثناء الملاحة.

لا يزال حساب المثلثات مستخدمًا في الملاحة من خلال وسائل مثل نظام التموضع العالمي (GPS) والذكاء الاصطناعي للمركبات الذاتية.

تُستخدم هذه المعادلة لتحديد المسافة بين نقطتين على الأرض:

$\mathrm {AB} =R\arccos \left[\sin \lambda _{\mathrm {A} }\,\sin \lambda _{\mathrm {B} }+\cos \lambda _{\mathrm {A} }\,\cos \lambda _{\mathrm {B} }\,\cos \left(L_{\mathrm {A} }-L_{\mathrm {B} }\right)\right]$

حيث:

• λ_A وλ_B هما خطا عرض النقطتين المرغوبتين.
• L_A وL_B هما خطا طول النقطتين المرغوبتين.
• R هو نصف قطر الأرض.

يمكن إثبات ذلك من قانون جيب التمام للمثلثات الكروية.

الفيزياء الميكانيكية

طالع أيضًا: حركة المقذوف وتصادم مرن

في الفيزياء الميكانيكية، تُطبق الدوال المثلثية على معادلات الحركة ثنائية الأبعاد وثلاثية الأبعاد، وحتى في دراسة حركة الأجسام. على سبيل المثال، عند تحليل الاختلافات الدورية في الحركيات والديناميكيات الدورانية، ومعادلات الزخم والزخم الزاوي، وظواهر التصادم، نستخدم فيها دوال مثلثية.

(5.ط) قذف جسم من مبدأ المَعْلم

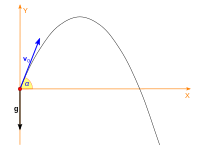
من أكثر التطبيقات المعروفة للدوال المثلثية في الميكانيكا هي دراسة ظاهرة حركة جسم مقذوف بزاوية α، وتكتب المعادلة الوسيطية لمسارها بدلالة الزمن t على النحو التالي:

$x(t)=v_{0}.t\cos \alpha$

$y(t)=-{\frac {1}{2}}gt^{2}+v_{0}.t\sin \alpha$

حيث x و y هي إحداثيات موضع الجسم عند t ثانية بعد السرعة الإبتدائية v₀، وg هو تسارع الجاذبية.

أيضا، يتم الحصول على سرعة الجسمين $v_{1}$ و $v_{2}$ ومقدار الزاويتين $\theta$ و$\varphi$ اللتين صنعهما الجسمان بعد التصادم المرن باستخدام الدوال المثلثية، بتطبيق قانون حفظ الزخم (في كلا المعادلتين، قبل تصادم جسمين (على اليسار) = بعد تصادم جسمين (على اليمين)):

$\to m_{1}v_{1}+0=m_{1}v'_{1}\cos \theta +m_{2}v'_{2}\cos \varphi$ ثابت $P_{x}=$ : على المحور x

$\to 0+0=m_{1}v'_{1}\sin \theta -m_{2}v'_{2}\sin \varphi$ ثابت $P_{y}=$ : على المحور y

القبلة

(5.ي) حساب القبلة من مدينة يوغياكارتا الإندونيسية.

القبلة هي وجهة المصلي عند الصلاة وهي عند المسلمين الكعبة المشرفة في مدينة مكة.

يتم تطبيق نموذج الدائرة العظمى لحساب القبلة باستخدام حساب المثلثات الكروية، وهو العلم الذي برع فيه العلماء المسلمين قديمًا واستقر العمل في تحديد القبلة عليه. في الشكل التالي، يشكل موقع المصلي O والكعبة Q والقطب الشمالي N مثلثًا على الكرة الأرضية. يُشار إلى القبلة بـ OQ، وهي اتجاه الدائرة العظمى التي تشمل النقطتين O و Q. يمكن أيضًا التعبير عن القبلة كالزاوية $\angle NOQ$ (أو $\angle q$) للقبلة بالنسبة للشمال، وتسمى أيضًا «إنحراف القبلة». يمكن حساب هذه الزاوية كدالة رياضية لخط عرض موقع المصلي $\Phi$، وخط عرض الكعبة $\Phi _{Q}$، والفرق بين خطي طول الموقعين المذكورين سابقًا $\Delta L$، هذه الدالة مستمدة من قاعدة ظل التمام التي تنطبق على أي مثلث كروي ذات الزوايا $A$، و $B$، و $C$ والجوانب $a$، و $b$، و $c$:

$\cos a\,\cos C=\cot b\,\sin a-\cot B\,\sin C$

بتطبيق هذه الصيغة على المثلث الكروي $\triangle NOQ$ (بتعويض $B=\angle q=\angle NOQ$) وبتطبيق المتطابقات المثلثية، نحصل على:

$\cot q={\frac {\sin \Phi \cos \Delta L-\cos \Phi \tan \Phi _{Q}}{\sin \Delta L}}$ ، ونستنتج من الصيغة السابقة أن:
$q=\cot ^{-1}{\frac {\sin \Phi \cos \Delta L-\cos \Phi \tan \Phi _{Q}}{\sin \Delta L}}$